Классы интегрируемых функций. Свойства определенного интеграла.

Виды функций для которых существует интеграл Римана.

I. Всякая непрерывная на отрезке функция является интегрируемой на этом отрезке.

II. Всякая монотонная на отрезке функция является интегрируемой на этом отрезке.

III. Функция, ограниченная на [a,b] и интегрируемая на любом отрезке [α,β ] ⊂ (a,b), интегрируема на отрезке [a,b]. Если функция y интегрируема на [a,b], то функция y1, определенная на [a,b] и совпадающая с y на ]a,b[, также интегрируема на [a,b], причем

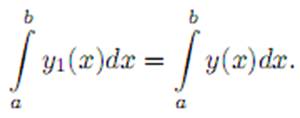
IV.Ограниченную функцию, заданную на отрезке [a,b], называют кусочно-монотонной, если существует такое разбиение X отрезка [a, b ], что на каждом интервале ]xk−1, xk [ этого разбиения функция монотонна.

Всякая кусочно-монотонная на [a,b] функция интегрируема на этом отрезке.

V. Всякая функция, определенная и ограниченная на отрезке и имеющая конечное число точек разрыва, интегрируема на этом отрезке. В частности, кусочно-непрерывная на отрезке функция интегрируема.

VI. Если функция y интегрируема на [a,b], то функция |y| также интегрируема на [a,b], т.е. y∈R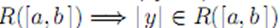

VII. Произведение интегрируемых функций является интегрируемой функцией, т.е.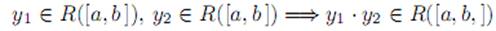

VIII. Пусть функция y : [a,b] → [c,d] интегрируема на [a,b], а функция z : [c,d] → R непрерывна. Тогда композиция z ◦ y : [a,b] → R интегрируема на [a,b].

Теорема 3.5 (Свойство аддитивности интеграла). Имеет место равенство

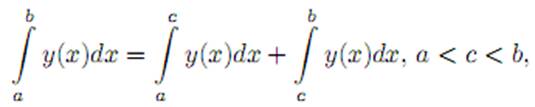
причем из существования интеграла в левой части этого равенства следует существование обоих интегралов в правой части и, наоборот, если оба интеграла справа существуют, то существует и интеграл слева.

Линейность интеграла.

Теорема 3.6.Пусть функции y1 и y2 интегрируемы на отрезке I с концами a и b. Тогда их линейная комбинация c1y1 + c2y2 с постоянными коэффициентами c1 и c2 также интегрируема на I, причем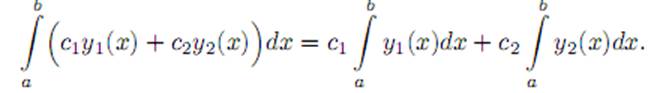

Монотонность интеграла.

Теорема 3.7. Если функции y1 и y2 интегрируемы на отрезке [a,b], a < b, и 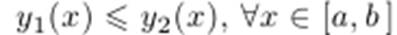то

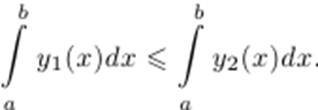
Аддитивность интеграла.

Теорема 3.9. Если a,b,c ∈ R и функция y интегрируема на отрезке I = [min{a, b, c}, max{a, b, c}], то справедливо следующее равенство .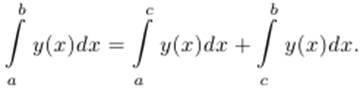

Интеграл с переменным верхним пределом.

Рассмотрим функцию y, интегрируемую на отрезке I и для фиксированного a∈ I положим 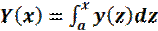, 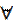x ∈ I. на отрезке I определена функция Y: x∈I ↦ 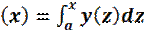, которую называют интегралом с переменным верхним пределом.

Теорема 3.12Интеграл с переменным верхним пределом от интегрируемой функции есть функция непрерывная.

Док-во: если 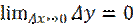, то ф-ция непрерывна. - =

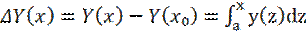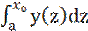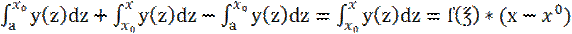
Теорема 3.13Если функция y ∈ R(I) и, кроме того, y непрерывна в точке x0 ∈ I, то функция Y дифференцируема в точке x0, причем Y‘(x0)= ( 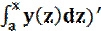= =y(x0)

Теорема 3.14 (Теорема о существовании первообразной). Для любой непрерывной на отрезке I функции y существует первообразная Y, определенная по формуле Y(x)= 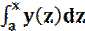, a ∈ I.

Теорема 3.15 (Формула Ньютона-Лейбница).Если функция y непрерывна на отрезке I с концами a и b, то

=

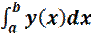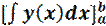
Док-во: F(x)=Y(x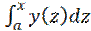)+C= +C 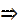F’(x)=Y’(x)+C’=y(x)

F(a)=Y(a)+C= 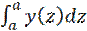+C=C ⇒ F(b)=Y(b)+C= 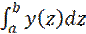+F(a)