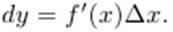Основные теоремы о дифференцируемых функциях. Правило Лопиталя.

Точки локального экстремума. Пусть c - точка из области определения функции.

Точку x0 называют точкой локального максимума функции f(x), если существует такая окрестность 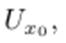что .

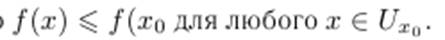Точку x0 называют точкой локального минимума функции f(x), если существует такая окрестность, что

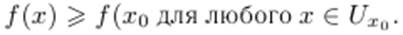
Точки локального максимума и локального минимума функции называют точками локального экстремума.

Стационарные точки функции. Пусть функция дифференцируема в точке c. Точка c называется стационарной точкой функции f(x), если .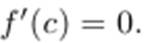

Теорема Ферма. Пусть функция f(x) определена на (a,b) и x0 ∈ (a,b) - точка локального экстремума. Если функция дифференцируема в точке x0, то x0 является стационарной точкой функции.

Теорема Ролля. Пусть функция f(x) непрерывна на [a,b] и дифференцируема на (a,b). Если f(a) = f(b), то на интервале (a,b) существует по крайней мере одна стационарная точка.

Конечные приращения. Пусть функция определена по меньшей мере на отрезке [a,b].

Теорема Лагранжа. Если функция f(x) непрерывна на [a,b] и дифференцируема на (a,b), то на (a,b), существует такая точка c, что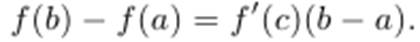

Если функция f(x) непрерывна на отрезке с концами a и b и дифференцируема внутри его, то существует такое число θ ∈ (0, 1), что 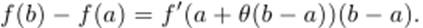Эту формулу называют формулой конечных приращений. Ее записывают также в виде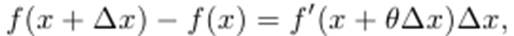

Теорема Коши. Если функции f(x) и g(x) непрерывны на [a,b], дифференцируемы на (a,b) и 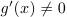на (a,b), то на (a,b), существует такая точка c, что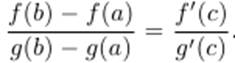

Правила Лопиталя

Пусть X - некоторый промежуток и a предельная точка множества X. Допускаем, что a может быть и +∞ или −∞. Рассмотрим функцию f(x), определенную на множестве 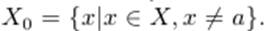Если a - граничная точка промежутка X, то при рассмотрении 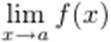рассматриваем соответствующий односторонний предел.

Первое правило Лопиталя. Пусть

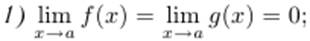
2) функции f(x) и g(x) дифференцируемы на X0;

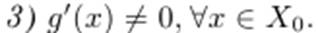
Если существует предел (конечный или бесконечны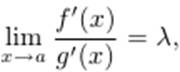й) то и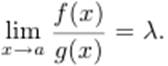

Второе правило Лопиталя. Пусть

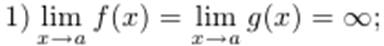
2) функции f(x) и g(x) дифференцируемы на X0;

3)

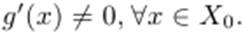
Если существует предел (конечный или бесконечны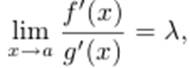й) то и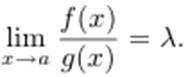

Производные высших порядков. Дифференциал. Дифференциалы высших порядков.

Последовательное дифференцирование

Для функции y = f(x) производной второго порядка называют производную функции 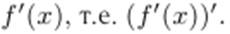Обозначают 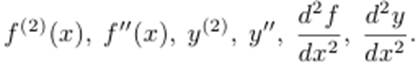Таким образом,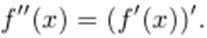

Для функции y = f(x) производной порядка n называют производную производной порядка n−1. Таким образом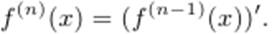

Теорема 2.36 (Формула Лейбница). Если функции u = u(x), v = v(x) имеют производные порядка n, то

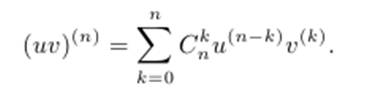
Дифференцирование функций, задаваемых параметрически

Теорема 2.37. Пусть формулы x = ϕ(t), y = ψ(t), t ∈ T задают параметрически функцию y = y(x). Если

функции ϕ(t) и ψ(t) дифференцируемы и ϕ’(t) =/ 0, то функция y = y(x) дифференцируема и ее производная y’(x) задается параметрически формулами

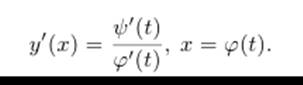
Дифференциалы

Дифференцируемость функции означает, что ее приращение представимо в виде ∆y = A · ∆x + o(∆x).

Главную часть приращения функции 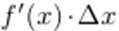называют дифференциалом и обозначают 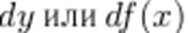Таким образом,