Матричные игры. Решение матричных игр в чистых стратегиях

Рассмотрим парную игру с нулевой суммой, в которой выигрыш одного игрока равен проигрышу другого.

У каждого игрока А и В конечное число возможных действий – чистых стратегий.

Игрок А располагает m чистыми стратегиями А₁, А₂, … , А_m. Игрок В – n чистыми стратегиями B₁, B₂, … , B_n. Игра определена, если указано правило, сопоставляющее каждой паре чистых стратегий A_i и B_j число a_ij – выигрыш игрока А за счет игрока B. При a_ij<0 игрок А платит игроку В сумму |a_ij|. Если известны значения a_ij выигрыша для каждой пары (A_i,B_j) стратегий, то можно составить матрицу игры – платежную матрицу.

Платежная матрица – это табличная запись функции выигрыша, исхода игры.

Ai Bj	B1	B2	B3	………………	Bn
A1	a11	a12	a13	………………	a1n
A2	a21	a22	a23	………………	a2n
…	…	…	…	………………
Am	am1	am2	am3	………………	amn

Целью игроков является выбор наиболее выгодных стратегий, доставляющих игроку А максимальный выигрыш, а игроку В минимальный проигрыш. В ТИ исходят из предположения, что каждый игрок считает своего противника разумным и стремящимся помешать ему достичь наилучшего результата.

Стратегию игрока А называют оптимальной, если при ее применении выигрыш игрока А не уменьшается, какими бы стратегиями не пользовался игрок В.

Оптимальной стратегией для игрока В называют стратегию, при использовании которой проигрыш игрока В не увеличивается, какие бы стратегии ни применял игрок А.

С учетом этого игрок А анализирует матрицу выигрышей: для каждой чистой стратегии А_i он определяет минимальное значение 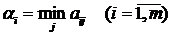. Затем по минимальным выигрышам α_i он отыскивает такую чистую стратегию А_i0, при которой этот минимальный выигрыш будет максимальным, т.е. находит

.

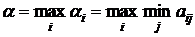Число α называется нижней чистой ценой игры (максимином). Оно показывает, какой минимальный выигрыш может получить игрок А, применяя свои чистые стратегии при любых действиях игрока В. Соответствующая стратегия А_i0 игрока А называется максиминной.

Игрок В старается максимально уменьшить проигрыш. Для каждой чистой стратегии В_j он отыскивает 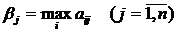. Затем по β_j находит свою стратегию B_j0, при которой его проигрыш будет минимальным, т.е.

.

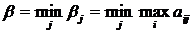Число β называется верхней чистой ценой игры (минимаксом). Оно показывает, какой максимальный проигрыш при использовании своих чистых стратегий может быть у игрока В. Соответствующая чистая стратегия B_j0 игрока B минимаксной.

Таким образом, используя чистые стратегии игрок А обеспечивает выигрыш не меньше α, а игрок B в результате применения своих чистых стратегий не позволит игроку выиграть больше, чем β. Принцип осторожности, диктующий игрокам выбор максиминной и минимаксной стратегий, называют принципом минимакса.

Пример. Найти максиминную и минимаксную стратегии в игре с матрицей

Решение.

	B1	B2	B3	В4	αi
A1			-1		-1
A2
A3			-2	-1	-2
βj

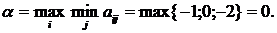
Максиминной чистой стратегией является А₂.

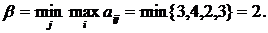
Минимаксной для игрока B является стратегия В₃.

Теорема 1. В матричной игре нижняя чистая цена игры не превосходит верхней чистой цены игры, т.е. α ≤ β.

Доказательство:

По определению

,

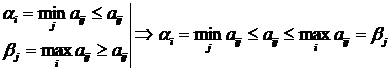значит α_i ≤ a_ij ≤ β_j или α_i ≤ β_j.

Это неравенство справедливо при любых комбинациях i и j. Будет оно справедливо для тех i и j, для которых 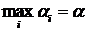и , и 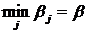при этих i и j получим α ≤ β.

Если в матричной игре нижняя и верхняя чистые цены игры совпадают, т.е. α = β, то это игра имеет седловую точку в чистых стратегиях и чистую цену игры .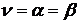

Обозначим через i_* и j_* номера чистых стратегий, при которых имеет место равенство α = β. Пару чистых стратегий 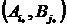игроков А и В, при которых достигается равенство α = β, называют седловой точкой матричной игры, а элемент a_i*j* матрицы, стоящий на пересечении i_* строки и j_* столбца, – седловым элементом платежной матрицы.

Седловой элемент 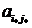является наименьшим в i_* строке и наибольшим в j_* столбце, т.е. 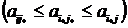. Поэтому, если игрок В отклонится от своей минимальной стратегии, то его проигрыш может увеличиться. Аналогично, отклонение игрока А от своей максимальной стратегии ведет к уменьшению его выигрыша. Таким образом, минимальные стратегии в игре с седловой точкой обладают свойством устойчивости, создают ситуацию равновесия. Следовательно, если в матрице игры существует седловой элемент, то наилучшими для игроков являются их минимальные стратегии. Назовем чистые стратеги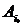и и 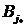, образующие седловой элемент, оптимальными чистыми стратегиями соответственно игроков А и В. Набор 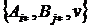назовем решением игры.

Пример. Швейное предприятие планирует к массовому выпуску новую модель одежды. Спрос на эту модель не может быть точно определен. Предполагают, что его величина характеризуется тремя возможными состояниями (I, II, III). С учетом этих состояний анализируется три возможных варианта выпуска данной модели (А₁, А₂, А₃). Каждый из этих вариантов требует своих затрат и обеспечивает различный эффект. Прибыль (тыс. руб.), которую получает предприятие при данном объеме выпуска модели и соответствующем состоянии спроса, определяется матрицей

	I	II	III
A1
A2
A3

Найти объем выпуска модели одежды обеспечивающий среднюю величину прибыли при любом состоянии спроса.

Решение. Проверим, имеет ли исходная матрица седловую точку.

.

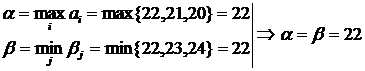Число 22 – цена игры. Игра имеет седловую точку, соответствующую варианту А₁ выпуска модели одежды. Объем выпуска модели, соответствующий данному варианту, обеспечивает прибыль в 22 тыс. руб. при любом состоянии спроса.

Упрощение игр

Если платежная матрица игры не содержит седловой точки, то задача определения оптимальной смешанной стратегии тем сложнее, чем больше размерность матрицы. Для игр с платежными матрицами большой размерности отыскание решения можно упростить, если уменьшить их размерность, вычеркивая дублирующие и заведомо невыгодные стратегии.

Если в матрице (a_ij)_m×n игры все элементы строки (столбца) равны соответствующим элементам другой строки (столбца), то соответствующие строкам (столбцам) стратегии называются дублирующими.

Если в матрице (a_ij)_m×n игры все элементы некоторой строки, определяющей i-ю стратегию А_i игрока А, не больше (меньше или равны) соответствующих элементов другой строки, то i-я стратегия А_i называется заведомо невыгодной.

Если в матрице (a_ij)_m×n игры все элементы некоторого столбца, определяющего j-ю стратегию В_j игрока В, не меньше (больше или равны) соответствующих элементов другого столбца, то j-я стратегия В_j называется заведомо невыгодной.

Рассмотрим платежную матрицу игры:

B1 B2 B3 В4 В5 αi A1 A2 A3 A4 βj

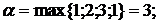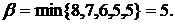α = 3 ≠ β = 5. Платежная матрица игры не имеет седловой точки.

Сравнивая почленно элементы второй и третьей строк, видим, что все элементы второй строки меньше соответствующих элементов третьей строки. Следовательно, вторая стратегия для игрока А заведомо невыгодна и ее можно исключить. Аналогично, сравнивая А₃ и А₄, исключаем А₄. Получаем матрицу игры:

	B1	B2	B3	В4	В5
A1
A3

Замечаем, что 1, 2, 3 стратегии игрока В заведомо невыгодны по сравнению с 5-й стратегией, поскольку игрок В стремится уменьшить выигрыш игрока А. Исключая эти стратегии, получаем матрицу 2×2, в которой нет дублирующих и заведомо невыгодных стратегий.

	В4	В5
A1
A3

Перенумеруем стратегии, запишем платежную матрицу:

В1 В2 αi A1 A2 βj

α = 3, β = 5.

Если для упрощенной матрицы α = β, то число α = β = v есть цена игры не только с упрощенной, но и со сходной матрицей. Если α < β, то анализируется упрощенная матрица, а затем осуществляется возвращение к исходной матрице.