Понятие матриц. Виды матрицы. Действия над матрицами.

Понятие матриц. Виды матрицы. Действия над матрицами.

Матрицей м на н называется прямоугольная система чисел содержащая м строк и н столбцов.

Числа составляющие матрицу наз. элементами матрицы и обознач. лат. буквами.

Виды: 1. матрица содержащая одну строку называется вектор строка, содерж. один столбец, вектор столбец; 2. матрица у которой число строк равно числу столбцов наз. кв. матрицей; 3. элементы которые соединяют верхний левый и нижний правый наз. элементами главной диагонали; 4. элементы кот. соединяют нижний левый и верхний правый наз. элементами побочной диагонали; 5. квадратная матрица наз. треугольной, если все элементы ниже главной диагонали равны 0; 6. если все не диагональные элементы матрицы равны 0 то матрица называется диагональной; 7. диагональная матрица все диагональные элементы кот. равны 1, называется единичной (E,I); 8. нулевой наз. матрицу если все элементы матрицы равны 0.

Действия над матрицами: 1. умножение матрица на число (произ. матрицы А на число λ наз. матрица В= λА, b11= λа11). 2. сложение матриц. суммой матриц одного размера А и В наз. матрица С того же размера кот. выч. по формуле С11=А11+В11. 3. вычитание матриц (разница 2-х матриц одного размера наз. матрица С вычисляемая по формуле. С=А-В=А+(-1)В; 4. произведением 2-х матриц А размером М на К и В размером К на Н называется матрица С размером М на Н. что бы найти элементы матрица С в i-строке и j-столбце, необходимо элементы i-строки 1 матрицы умножить на элементы j-столбца 2 матрицы. cij=a1ibi1+a2ib2j+…+aikbkj= ∑KS=1aisbsj. умножить матрицу можно тогда, когда кол-во столбцов одной матрицы равно кол-ву строк другой). 5.транспонирование (перемена строк и столбцов местами).

Определит. кв. матриц. Определен. и вычислен. определит. 2-го и 3-го порядка.

определит. – это число, характеризующ. кв. матрицу.

1. определителем кв. матриц. первого порядка А=(а11) , называется элемент а11 Δ1=|А|=а11.

2. определит. кв. матрицы второго порядка, наз. число которое вычисляется по формуле |А|=|матрица|=а11а22-а12а21.

3.определит. кв. матрицы 3-го порядка наз число выч. по формуле. |А|=|1 -2.

Система n ли-х ур-й с n неизвестными. Реш-е и использ. систем n линейных ур-й с n неизвест. по правилу Крамера.

кол-во ур-ний = кол-ву неизвестных.

в этом случае матрица А яв-ется квадратной, ее определитель яв-ется определит. системы.

Рас-м решение сист. двух ур-й с двумя переменными.

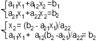
Для решения этой системы

умножим обе части ур-я на а22

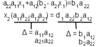
Δ, получается из определ. сист. из замены 1-го столбца на столбец линейной сист.

х1 = Δ1/ Δ, х2 = Δ2/ Δ

Теорема Крамера. Пусть Δ – определ. мытрицы сист. А, а Δj – определит. матрицы, получаемой из матрицы А заменой j-го столбца столбцом свободных членов. Тогда, если Δ≠0, то сист. имеет единст. решение, по формуле.

xj = Δj/ Δ j =1n

сист. n-линейного ур-я яв-ется определен. тогда и только тогда когда ее определит. отличен от 0.

2 сист. алгебраич. ур-й наз. эквивалентными если они имеют одинаковый набор решений.

Геометрич. вектор.

вектор –это направленный отрезок, который может перемещаться || самому себе; изображается →направленный от начала вектора к конце вектора.

длиной (модулем вектора) наз. число равное длине отрезка изабраж. вектора

2 вектора наз. равными если они соноправлены и имеют одну длину.

если начало и конец совпадают то этот вектор наз. нулевым.

всякий нулевой вектор имеет нулевую длину

только нулевой вектор имеет нулевую длину

направление нулевого вектора считается произвольным.

векторы наз. коллинеарными, если они лежат на одной прямой или на || прямых.

векторы наз. комплонарными если они лежат в одной плоскости или в || плоскостях.

2 вектора наз. ортогональными если угол между ними 90.

Линейные операции: 1. произведением вектора ā на число λ наз. новый вектор длина кот. |λR|=|λ||ā| и направление которого совпадает с направлением ā, если λ положительная и противоположна, если λ отрицательа |λR|=|λ||ā|

при умножении любого вектора на 0→получается нулевой вектор. 2. суммой 2-х векторов наз 3 вектор начало которого совпадает с началом 1-го вектора а конец с концом 2-го вектора при условии, что нач. 2-го вектора совмещено с концом 1-го. С=А+В

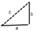
разностью 2-х векторов наз. сумма первого и 2-го умноженного на (-1) с=А-В

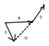
1. коммутативность а+в=В+А

2. дистубутивность уножения на число относительно сложения. λ(а+в)=λа+λв

3. дистрибутивность числовых сомножителей (λ+в)а = λа+ва

5. а-в= -(в-а)

13. Коллинеарные векторы.

векторы наз. коллинеарными, если они лежат на одной прямой или на || прямых.

необходимое и достаточ. условия коллиниарности 2-х векторов (2 вектора коллониарны тогда и только тогда, когда векторное произведение равно 0.

достаточно задать 2 вектора а остальные выразить

14 комплонарные вектора.

векторы наз. комплонарными если они лежат в одной плоскости или в || плоскостях

необходимое и достаточ. условие комплонарн 3-х векторов.

3 вектора компл. тогда и только тогад, когда их смешанное произведение равно 0.

достаточно задать 2 вектора а остальные выразить

Теорема о расположении вектора по 3 некомпланарным векторам. Теорема:всякий произвол в-ор dможно разложить по 3-ём некомплан векторам a,b,c.

Док-во: Пусть a,b,c-3 некомплан век-а,d – произвольный век-р. Возьмем в пространстве точку О. Отложим от нее ОА=а, ОВ=b,ОС=с, точки А,В,С не леж в одной плоскости.(С не принадл ОАВ). Пусть век-р d также не принадл ОАВ, тогда из В провед прям OD. Затем прям DD1 || OC, затем D1D2||OB, затем соед O и D2. Таким образом OD=OD2+D2D1+D1D(по построению).Т.к. OD2 коллин ОА, D2D1 коллин ОВ, D1D коллин ОС, отсюда следует что, OD2=xa, D2D1=yb, D1D=zc.

Отсюда OD=xa+yb+zc(*) ч.т.д.Единственность: предпол, что сущ x1,y1,z1такие, чтоOD=x1a+y1b+z1c(**).Приравняем (*) и (**)è(x-x1)a+(y-y1)b+(z-z1)c=0(0 это нулевой вектор). Предположим, что x1не=x, т.е. x-x1не=0, тогда а= -((y-y1)b/(x-x1) - (z-z1)c/(x-x1)), отсюда следует, что a,b,c-комплан, а это противор условию.Аналогично доказывается и y1 и z1.Следовательно x=x1, y=y1,z=z1.

Векторное произвед.

векторным произведением 2-х векторов наз. вектор, который удовлетворяет следующ. условию, его длина равна произведению длин векторов, на sin угла между ними.

данный вектор ортогонален обоим векторам.

он направлен таким образом, что если смотреть в его направление, то вращение вектора от 1 ко 2 происходит по часовой стрелке. обознач. АхВ

теорема: необходимое и достаточ. условия коллиниарности 2-х векторов (2 вектора коллониарны тогда и только тогда, когда векторное произведение равно 0.

Св-ва: 1.антикомуникативность АхВ= -В*А

2. числовой множитель можно выносить за знак векторного произведения. (λхА)хВ=λ(АхВ)

3. дистрибутивность относительно сумму. Ах(В+С)=АхВ+АхС

вырожение векторного произведения через координаты. пусть даны 2 вектора А={xzz}B{xzz}

разложим эти векторы через координаты

a = x1i+y1j+z1k b= x2i+y2j+z2k

вычислим векторное произведение.

АхВ= (x1i+y1j+z1k)х(x2i+y2j+z2k) = раскрыть. = вставить как вычис. вект. произведен. матрицу =

= х1у1k-x1z2j-y1x2k+y1z2i+z1x2j-z1y2i= (y1z2)i+(z1x2-x1z2)j+(x1y2-y1x2)k.

Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах

S=АхВ sinα

Смешанное произведение.

смеш.произ. наз число равное скалярн. произвед. на векторное.

Смешан. произвед. 3-ъ векторов наз. число вычисляемое по формуле.

АхВ*С = |матрица|

геометрич. смысл. модуль векторного произведения равен S пар-ма построенного на данных векторах. S=АхВ sinα

SΔ= половине (модуля) – векторного произведения. SΔ = ½ |АВхВС|

смешан. произвед. с точности до знака равно Vпаралепипеда, постоен. на данных векторах. V=Sосн*h

необходимое и достаточ. условие комплонарн 3-х векторов.

3 вектора компл. тогда и только тогад, когда их смешанное произведение равно 0. Св-ва: 1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. (а х b )•с=(b х с)•а=(с х а)•b. 2. Смешанное произведение меняет свой знак при перемене мест любых вух векторов-сомножителей, т. е. abc =-acb , abc =-bac , abc =-cba . 3. смешанное произведение ненулевых векторов а, b и с равно нулю огда и только тогда, когда они компланарны. Если abc =0 , то а, b и с— компланарны.

Понятие матриц. Виды матрицы. Действия над матрицами.

Матрицей м на н называется прямоугольная система чисел содержащая м строк и н столбцов.

Числа составляющие матрицу наз. элементами матрицы и обознач. лат. буквами.

Виды: 1. матрица содержащая одну строку называется вектор строка, содерж. один столбец, вектор столбец; 2. матрица у которой число строк равно числу столбцов наз. кв. матрицей; 3. элементы которые соединяют верхний левый и нижний правый наз. элементами главной диагонали; 4. элементы кот. соединяют нижний левый и верхний правый наз. элементами побочной диагонали; 5. квадратная матрица наз. треугольной, если все элементы ниже главной диагонали равны 0; 6. если все не диагональные элементы матрицы равны 0 то матрица называется диагональной; 7. диагональная матрица все диагональные элементы кот. равны 1, называется единичной (E,I); 8. нулевой наз. матрицу если все элементы матрицы равны 0.

Действия над матрицами: 1. умножение матрица на число (произ. матрицы А на число λ наз. матрица В= λА, b11= λа11). 2. сложение матриц. суммой матриц одного размера А и В наз. матрица С того же размера кот. выч. по формуле С11=А11+В11. 3. вычитание матриц (разница 2-х матриц одного размера наз. матрица С вычисляемая по формуле. С=А-В=А+(-1)В; 4. произведением 2-х матриц А размером М на К и В размером К на Н называется матрица С размером М на Н. что бы найти элементы матрица С в i-строке и j-столбце, необходимо элементы i-строки 1 матрицы умножить на элементы j-столбца 2 матрицы. cij=a1ibi1+a2ib2j+…+aikbkj= ∑KS=1aisbsj. умножить матрицу можно тогда, когда кол-во столбцов одной матрицы равно кол-ву строк другой). 5.транспонирование (перемена строк и столбцов местами).