Точки разрыва функции и их классификация. Непрерывность элементарных функций.

38¹. Точки разрыва функции и их классификация.

Точка а называется точкой разрыва функции , если функция не является непрерывной в этой точке.

Если 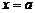– точка разрыва функции 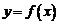, то в ней не выполняется, по крайней мере, одно из условий первого определения непрерывности функции, а именно:

1. Функция определена в некоторой окрестности точки а, но не определена в самой точке а.

Например, функция 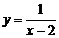не определена в точке 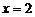(рис. 1).

Рис. 1

Рис. 2

2. Функция определена в точке а и ее окрестности, но не существует предела 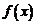при .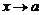

Например, функция

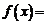
(1)

определена в точке 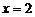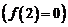, однако в точке 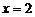имеет разрыв (рис. 2), т. к. эта функция не имеет предела в этой точке:

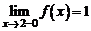, а .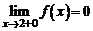

3. Функция определена в точке а и ее окрестности и существует .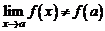

Например, рассмотрим функцию (рис. 3)

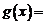
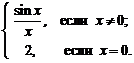(2)

Рис. 3

Здесь 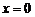– точка разрыва функции 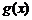, т.к. 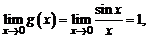а .

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.

Точка а называется точкой разрыва первого рода функции 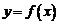, если в этой точке существуют конечные пределы функции слева и справа, т.е. 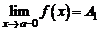и . При этом:

а) если 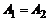, то точка а называется точкой устранимого разрыва; б) если , то точка а называется точкой конечного разрыва. Величину 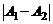называют скачком функции в точке разрыва .

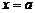Точка а называется точкой разрыва второго рода функции 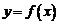, если по крайней мере один из односторонних пределов (слева или справа) не существует.

Так, функция 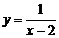(рис. 1) имеет разрыв второго рода в точке 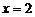. Для функции (1) (рис. 2) точка 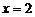является точкой разрыва первого рода со скачком, равным 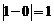. Точка 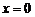является точкой разрыва первого рода для функции (2) (рис. 3). Положив (вместо ) при 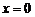, разрыв устранится, функция станет непрерывной в точке .

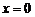38². Непрерывность элементарных функций.

Разумеется, имеется бесконечно много разных функций. Однако среди них выделяется класс элементарных функций. К ним относятся:

а) степенная функция у=xⁿ;

Функция y=x^m, где m – произвольное вещественное число, называется степенной функцией. В общем случае считается, что она определена для x>0, хотя при некоторых частных значениях m (например, когда m - целое число) она имеет смысл и при x<0.

Графики этой функции имеют различный вид при разных m.

а) 0<m<1.В этом случае y=x^m определена для x³ 0. Она является строго монотонно возрастающей функцией и непрерывна для всех x³ 0.

б) m>1.В этом случае y=x^m определена для x³ 0. Она является строго монотонно возрастающей функцией и непрерывна для всех x³ 0.

б) m<0.В этом случае y=x^m определена для всех x>0 и . Она является строго монотонно убывающей функцией и непрерывна для всех x>0.

б) показательная функция у=a^x;

Функция y=a^x называется показательной функцией. Число a является произвольным положительным вещественным числом, т.е. a>0. Функция определена и непрерывна для всех вещественных х. Ее графики имеют различный вид в зависимости от значения а.

При a>1 y=a^x строго монотонно возрастает.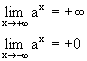

При 0<a<1 y=a^x строго монотонно убывает.

Основным свойством показательной функции является следующее свойство:

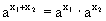
Можно показать, что среди непрерывных функций показательная функция – единственная функция, удовлетворяющая свойству f(x₁+x₂)=f(x₁)f(x₂).

Следствием этого свойства является следующее: (a^x)^m=a^xm

в) логарифмическая функция у=log_a(x);

Функция, обратная a^x, называется логарифмической функцией, и обозначается log_ax. Ее свойства получаются как следствия свойств функции a^x.

а) а>0

Так как a^x строго непрерывна, то и log_ax тоже непрерывна.

б)0<x<1

log _ax непрерывна.

Можно показать, что log_ax – единственная непрерывная функция, удовлетворяющая свойству.

г) гиперболические функции sh(x), ch(x), th(x);

С функцией e^x тесно связаны функции, получившие название гиперболических. К ним относятся:

гиперболический синус

гиперболический косинус

гиперболический тангенс

Рассмотрим коротко свойства этих функций.

1. Область определения этих функций -¥<x<+¥
2. sh(-x)= –sh(x)

th(-x)= –th(x)

ch(-x)= ch(x)

т.е. sh(x) и th(x) являются нечетными функциями, а ch(x) – четной функцией. Графики их изображены на рисунках.

1. sh(h), ch(x), и th(x) непрерывны для всех х.
2. sh(x) и th(x) монотонно возрастают.
3. Выведем основные формулы, касающиеся этих функций, и очень напоминающие формулы тригонометрии.

д) тригонометрические функции sin(x), cos(x), tg(x);

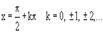Т.к. эти функции подробно изучаются в школе, то напоминать их свойства мы не будем. Укажем лишь, что sinus(x) и cos(x) непрерывны для всех x, а имеет разрывы второго рода в точках, где cos(x)=0, т.е. в точках