Функции, непрерывные на отрезке, и их свойства
Функция  называется непрерывной на интервале
называется непрерывной на интервале 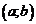 , если она непрерывна в каждой точке
, если она непрерывна в каждой точке 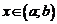 . Если же, кроме того, функция
. Если же, кроме того, функция  непрерывна в точке а справа, а в точке
непрерывна в точке а справа, а в точке 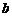 – слева, то функция
– слева, то функция  называется непрерывной на отрезке
называется непрерывной на отрезке  .
.
Функция  называется кусочно-непрерывной на отрезке
называется кусочно-непрерывной на отрезке  , если она непрерывна во всех внутренних точках
, если она непрерывна во всех внутренних точках  , за исключением конечного числа точек, в которых она имеет разрывы первого рода, а в точках а и
, за исключением конечного числа точек, в которых она имеет разрывы первого рода, а в точках а и 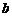 имеет соответствующие односторонние пределы.
имеет соответствующие односторонние пределы.
Утверждение 1. Монотонная на отрезке  функция
функция  может иметь точки разрыва только первого рода.
может иметь точки разрыва только первого рода.
Согласно этому утверждению, множество значений монотонной функции будет отрезком в том и только в том случае, если  – непрерывная функция на отрезке
– непрерывная функция на отрезке  .
.
Утверждение 2 (об устойчивости знака непрерывной функции). Пусть функция  непрерывна в точке
непрерывна в точке 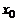 и
и  . Тогда существует
. Тогда существует 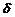 -окрестность точки
-окрестность точки 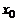 , такая, что в этой окрестности функция
, такая, что в этой окрестности функция  имеет тот же знак, что и
имеет тот же знак, что и 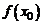 .
.
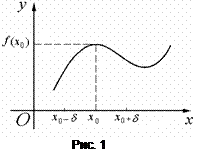 Геометрический смысл этого утверждения состоит в том, что, если функция
Геометрический смысл этого утверждения состоит в том, что, если функция  непрерывна в точке
непрерывна в точке 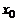 и отлична в ней от нуля, то некоторая часть графика этой функции, проходящая через точку
и отлична в ней от нуля, то некоторая часть графика этой функции, проходящая через точку 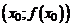 , не пересекает ось
, не пересекает ось 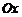 (рис. 1).
(рис. 1).
Теорема 1 (первая теорема Больцано-Коши).Пусть функция  непрерывна на отрезке
непрерывна на отрезке  и на концах отрезка имеет значения разных знаков. Тогда существует точка
и на концах отрезка имеет значения разных знаков. Тогда существует точка 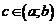 , в которой
, в которой 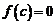 .
.
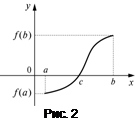
 Геометрический смысл этой теоремы также очевиден. Поскольку функция
Геометрический смысл этой теоремы также очевиден. Поскольку функция 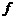 непрерывна на отрезке, то ее график состоит из одного «сплошного» куска. Эта кривая соединяет точки
непрерывна на отрезке, то ее график состоит из одного «сплошного» куска. Эта кривая соединяет точки 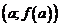 ,
, 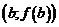 , одна из которых лежит ниже оси Ox, вторая – выше оси Ox. Следовательно, существует точка с на оси Ox, в которой график пересекает ось Ox (рис. 2).
, одна из которых лежит ниже оси Ox, вторая – выше оси Ox. Следовательно, существует точка с на оси Ox, в которой график пересекает ось Ox (рис. 2).
 Теорема 2 (вторая теорема Больцано-Коши).Пусть функция
Теорема 2 (вторая теорема Больцано-Коши).Пусть функция  непрерывна на отрезке
непрерывна на отрезке 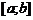 , причем
, причем 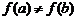 . Тогда, если С – любое число, лежащее строго между
. Тогда, если С – любое число, лежащее строго между 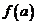 и
и 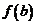 , то существует точка
, то существует точка 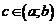 , такая, что
, такая, что 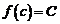 .
.
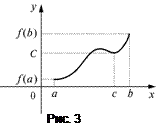
Другими словами, непрерывная на отрезке  функция принимает любое свое промежуточное значение.
функция принимает любое свое промежуточное значение.
Геометрический смысл этой теоремы показан на рис. 3.
372. Свойства функций, непрерывных в точке.
Основные свойства функций, непрерывных в точке, непосредственно следуют из соответствующих свойств их пределов.
Свойство 1. Пусть функции  и
и 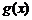 непрерывны в точке
непрерывны в точке 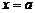 . Тогда функции
. Тогда функции 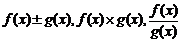 также непрерывны в этой точке (последняя при условии, что
также непрерывны в этой точке (последняя при условии, что 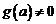 ).
).
Свойство 2. Пусть функция 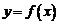 непрерывна в точке
непрерывна в точке 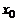 , а функция
, а функция 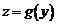 непрерывна в точке
непрерывна в точке 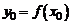 . Тогда сложная функция
. Тогда сложная функция 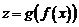 непрерывна в точке
непрерывна в точке 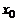 .
.
Непрерывность элементарных функций.Эементарной называется такая функция, которую можно задать одной формулой, содержащей конечное число арифметических действий и суперпозиций (операция взятия функции от функции) основных элементарных функций. Поэтому из приведенных свойств о пределах и непрерывности функций вытекает, что всякая элементарная функция непрерывна в каждой точке, в которой она определена.
Этот результат позволяет легко находить пределы элементарных функций в точках, где они определены.
