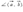Скалярное произведение векторов. Угол между векторами. Условие параллельности или перпендикулярности векторов.

Скалярное произведение векторов. Угол между векторами. Условие параллельности или перпендикулярности векторов.

Скалярным произведением векторов называется произведение их длин на косинус угла между ними:

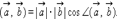Совершенно аналогично, как в планиметрии, доказываются следующие утверждения:

Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

Скалярный квадрат вектора, то есть скалярное произведение его самого на себя, равно квадрату его длины.

Скалярное произведение двух векторов 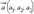и 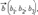заданных своими координатами, может быть вычислено по формуле

Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю. Пример. Даны два вектора и 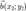. Эти векторы будут перпендикулярны, если выражение x1x2 + y1y2 = 0.Углом между ненулевыми векторами называется угол между прямыми, для которых данные вектора являются направляющими. Угол между любым вектором и нулевым вектором по определению считаем равным нулю. Если угол между векторами равен 90°, то такие вектора называются перпендикулярными. Угол между векторами будем обозначать так: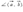

Условие перпендикулярности векторов

- Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.

- Даны два вектора a(xa;ya) и b(xb;yb). Эти векторы будут перпендикулярны, если выражение xaxb + yayb = 0.

Вектора параллельны, если их векторное произведение равно нулю

Уравнение прямой на плоскости. Основные задачи на прямую на плоскости.

Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2  0. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:- C = 0, А  0, В  0 – прямая проходит через начало координат- А = 0, В  0, С  0 { By

+ C = 0}- прямая параллельна оси Ох- В = 0, А  0, С  0 { Ax + C = 0} – прямая параллельна оси Оу- В = С = 0, А  0 – прямая совпадает с осью Оу- А = С = 0, В  0 – прямая совпадает с осью Ох Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.

Если хотя бы один из коэффициентов А, В,С ур-я Ах+Ву+С=0 равен 0, ур-е
наз. неполным. По виду уравнения прямой можно судить о ее положении на
плоксоти ОХУ. Возможны случаи:
1 С=0 L: Ax+By=0 т. О(0,0) удовлетворяет этому уравнению значит прямая
проходит через начало координат
2 А=0 L: Ву+С=0 - нормальный в-р n={0,B} перпендикулярен оси ОХ отсюда
следует, что прямая параллельна ось ОХ
3 В = 0 L: Ay+C=0 0 - номральный в-р n={А,0} перпендикулярен оси ОY отсюда
следует, что прямая параллельна ось ОУ
4 А=0, С=0 L: By=0(y=0(L=OX
5 B=0, C=0 L: Ax=0(x=0(L=OY
6 A ( 0, В ( 0, С ( 0 L; - не проходит через начало координат и пересекает
обе оси.

Уравнение прямой　на плоскости, проходящей через две заданные точк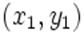и и :

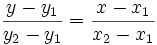
Угол между плоскостями.

Вычесление определителей

Вычисление определителей основывается на их известных свойствах, которые относятся к определителям всех порядков. Вот эти свойства:

1. Если переставить две строки (или два столбца) определителя, то определитель изменит знак.

2. Если соответствующие элементы двух столбцов (или двух строк) определителя равны или пропорциональны, то определитель равен нулю.

3. Значение определителя не изменится, если поменять местами строки и столбцы, сохранив их порядок.

4. Если все элементы какой-либо строки (или столбца) имеют общий множитель, то его можно вынести за знак определителя.

5. Значение определителя не изменится, если к элементам одной строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число.

Матрица и дей-ия над ними

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Обычно матрицы представляются двумерными (прямоугольными) таблицами. Иногда рассматривают многомерные матрицы или матрицы непрямоугольной формы.

Обычно матрицу обозначают заглавной буквой латинского алфавита и выделяют круглыми скобками «(…)» (встречается также выделение квадратными скобками «[…]» или двойными прямыми линиями "||…||").

Числа, составляющие матрицу (элементы матрицы), часто обозначают той же буквой, что и саму матрицу, но строчной (к примеру a11 является элементом матрицы А).

У каждого элемента матрицы есть 2 нижних индекса (aij) — первый «i» обозначает номер строки, в которой находится элемент, а второй «j» — номер столбца. Говорят «матрица размерности », подразумевая, что в матрице m строк и n столбцов. В одной матрице всегда ,

Операции над матрицами

Пусть aij — элементы матрицы A, а bij — элементы матрицы B.

Линейные операции:

Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен

bij = λaij

Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен

cij = aij + bij

Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы C, элементы которой

cij = aij - bij

Сложение и вычитание допускается только для матриц одинакового размера.

Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть

A + Θ = A

Все элементы нулевой матрицы равны нулю.

Нелинейные операции:

Умножение матриц (обозначение: AB, реже со знаком умножения ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.cij = ∑ aikbkj k

В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность , B — , то размерность их произведения AB = C есть . Умножение матриц не коммутативно.

Умножение матриц ассоциативно. Возводить в степень можно только квадратные матрицы.

Транспонирование матрицы (обозначение: AT) — операция, при которой матрица отражается относительно главной диагонали, то есть

Если A — матрица размера , то AT — матрица раз мера

Производная сложной функции

Сложная функция имеет вид: F(x) = f(g(x)), т.е. является функцией от функции. Например, y = sin2x, y = ln(x2+2x) и т.д.

Если в точке х функция g(x) производную g'(x) , а в точке u = g(x) функция f(u) имеет производную f'(u), то производная сложной функции f(g(x)) в точке х существует и равна f'(u)g'(x).

Производная неявной функции

Во многих задачах функция y(x) задана невным образом. Например, для приведенных ниже функций

невозможно получить зависимость y(x) в явном виде.

Алгоритм вычисления производной y'(x) от неявной функции выглядит следующим образом:

-Сначала необходимо продифференцировать обе части уравнения по отношению к x, предполагая, что y - это дифференцируемая функция x и используя правило вычисления производной от сложной функции;

-Решить полученное уравнение относительно производной y'(x).

Рассмотрим для иллюстрации несколько примеров.

Пример 1

Продифференцировать функцию y(x), заданную уравнением .

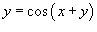
Решение.

Продифференцируем обе части уравнения по переменной x:

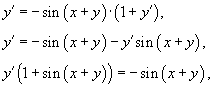
что приводит к результату

Правило Лапиталя

Правило Лопиталя. Пусть ф-ция f(x) и g(x) имеет в окр. т-ки х0 пр-ные f‘ и g‘ исключая возможность саму эту т-ку х0. Пусть lim(х®Dх )=lim(x®Dx)g(x)=0 так что f(x)/g(x) при x®x0 дает 0/0. lim(x®x0)f‘(x)/g‘(x) $ (4), когда он совпадает с пределом отношения ф-ции lim(x®x0)f(x)/g(x)= lim(x®x0)f‘(x)/g‘(x) (5)

44.1.(Критерий монотонности функции, имеющей производную на интервале) Пусть функция 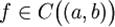непрерывна на

(a,b), и имеет в каждой точке производную f'(x). Тогда

1)f возрастает на (a,b) тогда и только тогда, когда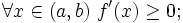

2) убывает на (a,b) тогда и только тогда, когда

2. (Достаточное условие строгой монотонности функции, имеющей производную на интервале) Пусть функция непрерывна на (a,b), и имеет в каждой точке производную f'(x). Тогда

1) если 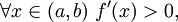то f строго возрастает на (a,b);

2) если то f строго убывает на (a,b).

Обратное, вообще говоря, неверно. Производная строго монотонной функции может обращаться в ноль. Однако, множество точек, где производная не равна нулю, должно быть плотно на интервале (a,b). Точнее имеет место.

3. (Критерий строгой монотонности функции, имеющей производную на интервале) Пусть и всюду на интервале определена производная f'(x). Тогда f строго возрастает на интервале (a,b) тогда и только тогда, когда выполнены следующие два условия:

1)

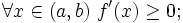
2)

Скалярное произведение векторов. Угол между векторами. Условие параллельности или перпендикулярности векторов.

Скалярным произведением векторов называется произведение их длин на косинус угла между ними:

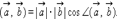Совершенно аналогично, как в планиметрии, доказываются следующие утверждения:

Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

Скалярный квадрат вектора, то есть скалярное произведение его самого на себя, равно квадрату его длины.

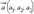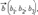Скалярное произведение двух векторов и заданных своими координатами, может быть вычислено по формуле

Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю. Пример. Даны два вектора и 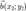. Эти векторы будут перпендикулярны, если выражение x1x2 + y1y2 = 0.Углом между ненулевыми векторами называется угол между прямыми, для которых данные вектора являются направляющими. Угол между любым вектором и нулевым вектором по определению считаем равным нулю. Если угол между векторами равен 90°, то такие вектора называются перпендикулярными. Угол между векторами будем обозначать так: