D. Законы распределения дискретных случайных величин.

1. Вероятность того, что стрелок попадет в мишень при одном выстреле, равна 0,8. Стрелку выдают патроны, пока он не промахнется, но не более пяти патронов. Найти закон распределения, М(Х), Д(Х) числа попаданий в мишень.

2. Испытуемый прибор состоит из 3 малонадежных элементов. Отказы элементов за время Т независимы, а их вероятности равны соответственно 0,1; 0,2; 0,25. Найти закон распределения, М(Х), Д(Х) числа отказавших за время Т элементов.

3. Известно, что в партии из 20 телефонных аппаратов имеется 5 неисправных. Из партии выбрано 4 аппарата. Найти закон распределения, М(Х), Д(Х) числа неисправных аппаратов среди отобранных.

4. Производится ряд выстрелов по мишени с вероятностями попадания 0,8 при каждом выстреле. Стрельба ведется до первого попадания в мишень, но не более 4 выстрелов. Найти закон распределения, М(Х), Д(Х) числа произведенных выстрелов.

5. Студент купил 4 билета новогодней лотереи. Вероятность выигрыша по одному билету равна 0,6. Найти закон распределения, М(Х), Д(Х) числа выигрышей.

6. Обрыв связи произошел на одном из пяти звеньев телефонного кабеля. Монтер последовательно проверяет все звенья для обнаружения места обрыва. Составить закон распределения, М(Х), Д(Х) числа обследованных звеньев, если вероятность обрыва связи одинакова для всех звеньев.

7. Охотник стреляет по дичи до первого попадания, но успевает сделать не более 4 выстрелов. Составить закон распределения, найти М(Х), Д(Х) числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7.

8. Каждая партия, состоящая из 21 прибора, содержит 7 неточных. Из 5 партий случайным образом отобрано по одному прибору. Найти закон распределения, М(Х), Д(Х) числа точных приборов среди отобранных.

9. Вероятность попадания в цель из орудия при первом выстреле равна 0,1, при втором -0,4, при третьем- 0,7. Предполагается произвести 3 выстрела. Найти закон распределения, М(Х), Д(Х) числа попаданий в цель.

10. Имеется 4 заготовки для одной и той же детали. Вероятность изготовления годной детали из каждой заготовки равна 0,7. Найти закон распределения, М(Х), Д(Х) числа заготовок, оставшихся после изготовления годной детали.

11. Баскетболист бросает мяч в корзину до первого попадания, но делает не более трех бросков. Составить закон распределения случайной величины Х – числа бросков, найти математическое ожидание М(Х) и дисперсию D(Х), если вероятность попадания при каждом броске равна 0,6.

12. Вероятность появления герба при одном подбрасывании монетки равна 0,5. Монета подбрасывается 3 раза. Составить закон распределения случайной величины Х – числа выпавших гербов, найти математическое ожидание М(Х) и дисперсию D(Х).

13. Рабочий обслуживает 3 станка. Вероятность того, что 1-й станок потребует внимание рабочего в течение часа, равна 0,6. Для 2-го станка эта вероятность равна 0,7; для 3-го станка – 0,8. Составить закон распределения случайной величины Х – числа станков, потребующих внимания рабочего в течение часа, найти математическое ожидание М(Х) и дисперсию D(Х).

14. Вероятность рождения мальчика равна 0,5. В семье 3 детей. Составить закон распределения случайной величины Х – числа мальчиков в этой семье, найти математическое ожидание М(Х) и дисперсию D(Х).

15. Имеется 3 заготовки для деталей. Вероятность изготовления годной детали из каждой заготовки 0,7. Составить закон распределения случайной величины Х – числа заготовок, оставшихся после изготовления годной детали, найти математическое ожидание М(Х) и дисперсию D(Х).

16. Вероятность того, что в библиотеке необходимая студенту книга свободна, равна 0,3. В городе три библиотеки. Составить закон распределения случайной величины Х – числа библиотек, которые посетит студент, найти математическое ожидание М(Х) и дисперсию D(Х).

17. Производится стрельба по мишени с вероятностью попадания в цель при каждом выстреле 0,6. Всего произведено 3 выстрела. Составить закон распределения случайной величины Х – числа попаданий в мишень, найти математическое ожидание М(Х) и дисперсию D(Х).

18. Прибор содержит три малонадежных элемента. Отказы элементов за некоторое время Т независимы, а их вероятности равны соответственно р₁=0,1, р₂=0,2, р₃=0,25.Составить закон распределения случайной величины Х – числа отказавших за время Т элементов, найти математическое ожидание М(Х) и дисперсию D(Х).

19. Куплено 3 лотерейных билета. Вероятность выигрыша по одному билету равна 0,2. Составить закон распределения случайной величины Х – числа проигрышных билетов, найти математическое ожидание М(Х) и дисперсию D(Х).

20 Дискретная случайная величина Х может принимать только два значения : х₁ и х₂ , причем х₁ < х₂ . Известны вероятность р₁ = 0,3 возможного значения х₁ , математическое ожидание М(х) = 3,7 и дисперсия Д(х) = 0,21. найти закон распределения этой случайной величины.

21. Найти математическое ожидание и дисперсию случайной величины Х, заданной таблично

Х	-5
Р	0,4	0,3	0,1	0,2

22. Дискретная случайная величина Х может принимать только два значения : х₁ и х₂ , причем х₁ < х₂ . Известны вероятность р₁ = 0,3 возможного значения х₁ , математическое ожидание М(х) = 3,7 и дисперсия Д(х) = 0,21. найти закон распределения этой случайной величины.

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

1) Дано статистическое распределение выборки: в первой строке указаны выборочные варианты х_i , а во второй строке – соответственные частоты n_i количественного признака Х). Требуется найти:

1. Методом произведений: а) выборочную среднюю; б) выборочное среднее квадратическое отклонение;

2. Доверительные интервалы для оценки неизвестного математического ожидания а с заданной надежностью g=0,95.

3. Пользуясь критерием Пирсона, при уровне значимости a=0,05, установить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с данными выборки объема n=100:

1.1)

хi
ni

1.2)

хi	10,6	15,6	20,6	25,6	30,6	35,6	40,6
ni

1.3)

хi
ni

1.4)

хi	12,4	16,4	20,4	24,4	28,4	32,4	36,4
ni

1.5)

хi
ni

1.6)

хi
ni

1.7)

хi	10,2	10,9	11,6	12,3		13,7	14,4
ni

1.8)

хi	11,5		12,5		13,5		14,5
ni

1.9)

хi
ni

1.10)

хi
ni

1.11)

хi	12,5		13,5		14,5		15,5
ni

1.12)

хi
ni

2. Найти по данной корреляционной таблице:

а) выборочное уравнение прямой 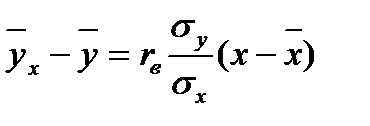регрессии Y на Х;

б) выборочное корреляционное отношение 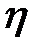_YX

2.1)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100

2.2)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100

2.3)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100

2.4)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100

2.5)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100

2.6)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100

2.7)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100

2.8)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100

2.9)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100

2.10)

Y	X	ny
-3	-2	-1
-2			-	-	-	-
-1	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
nx							n=100