Дифференциалы высших порядков.
Пусть y=f(x) дифференцируемая функция, а ее аргумент x – независимая переменная. Тогда ее первый дифференциал dyесть также функция x и можно найти дифференциал этой функции. Дифференциал от дифференциала функции y=f(x) называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается d^2y. По определениям дифференциалов 1 и 2 пор.: d^2y=d(dy)=d(f’(x)dx)=(f’(x)dx)’*dx=f”(x)dx*dx=f”(x)(dx)^2=f”(x)dx^2
Аналогично можно вывести выражение для d^3y: d^3y=fm(x)dx^3
В общем случае: d^ny=f^(n) (x) dx^n
20. Основные теоремы дифференциального исчисления. Теорема Ферма (док.)
Теорема Ферма. Пусть функция 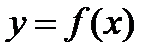 определена и дифференцируема на интервале (а,в) и в некоторой точке
определена и дифференцируема на интервале (а,в) и в некоторой точке 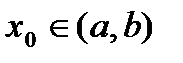 принимает наибольшее или наименьшее значение. Тогда
принимает наибольшее или наименьшее значение. Тогда 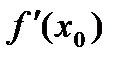 =0.
=0.
Док-во. Пусть 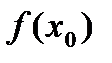 - наибольшее значение функции на интервале (а,в). Тогда при
- наибольшее значение функции на интервале (а,в). Тогда при 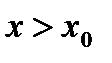 :
:
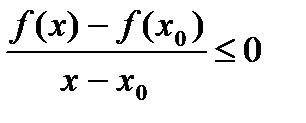 ,
, 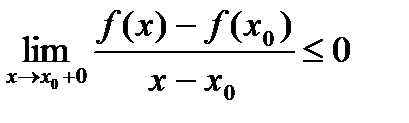 .
.
При 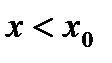 :
: 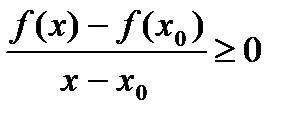 ,
, 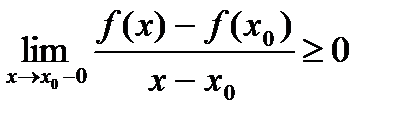 .
.
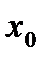 |
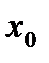 , то указанные выше пределы должны совпадать. А это возможно лишь при
, то указанные выше пределы должны совпадать. А это возможно лишь при 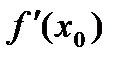 =0.
=0. Геометрически теорема Ферма означает, что в точках наибольшего или наименьшего значений дифференцируемой функции касательная к графику функции имеет нулевой угловой коэффициент, т.е. параллельна оси Ох.
Основные теоремы дифференциального исчисления. Теорема Ролля
Теорема Ролля (о среднем). Пусть функция 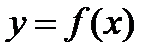 :
:
1) непрерывна на отрезке 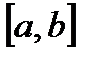 ;
;
2) дифференцируема на интервале 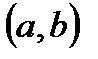 ;
;
3) принимает на концах интервала равные значения: f(a)=f(b).
Тогда существует т. 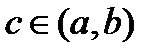 , такая, что
, такая, что 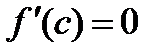 .
.
Док-во. По второй теореме Вейерштрасса непрерывная на отрезке функция достигает на нем своего наибольшего и наименьшего значений. Если оба эти значения достигаются на концах отрезка, а по условию они равны, следовательно, функция постоянна и ее производная равна нулю. Если хотя бы одно из этих значений достигается внутри отрезка, то 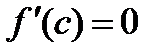 по теореме Ферма.
по теореме Ферма.
Замечание. Если f(a)=f(b)=0, то теорему Ролля можно сформулировать так: между двумя последовательными нулями дифференцируемой функции имеется хотя бы один нуль производной.
Основные теоремы дифференциального исчисления. Теорема Лагранжа
Теорема Лагранжа (о среднем). Пусть функция 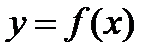 :
:
1) непрерывна на отрезке 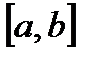 ;
;
2) дифференцируема на интервале 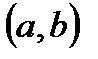 .
.
Тогда существует т. 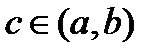 , такая, что
, такая, что 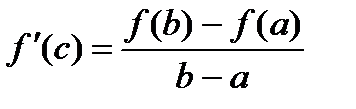 .
.
(или 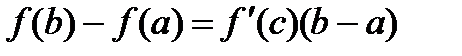 , эта формула называется формулой конечных приращений).
, эта формула называется формулой конечных приращений).
| х |
| В |
| А |
| с |
| в |
| а |
| у |
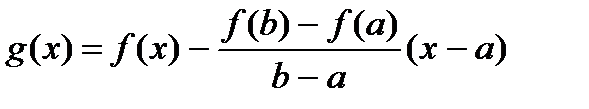 . Она непрерывна на отрезке
. Она непрерывна на отрезке 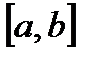 , дифференцируема на интервале
, дифференцируема на интервале 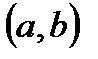 и g(a)=g(b). Т.о., эта функция удовлетворяет условиям теоремы Ролля. Следовательно, существует т.
и g(a)=g(b). Т.о., эта функция удовлетворяет условиям теоремы Ролля. Следовательно, существует т. 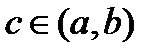 , такая, что
, такая, что 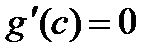 или:
или: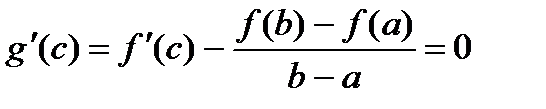 , откуда
, откуда 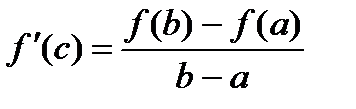 .
.
Геометрический смысл теоремы Лагранжа состоит в следующем.
Производная 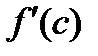 - это тангенс наклона касательной в точке с.
- это тангенс наклона касательной в точке с.
А отношение 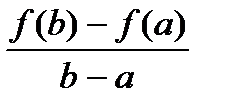 - это тангенс наклона секущей, проходящей через точки А и В. Тогда теорема означает, что на интервале (а,в) найдется точка с, в которой касательная параллельна секущей АВ.
- это тангенс наклона секущей, проходящей через точки А и В. Тогда теорема означает, что на интервале (а,в) найдется точка с, в которой касательная параллельна секущей АВ.
