Линейная зависимость векторов.

Векторы 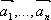называются линейно зависимыми, если существует такая линейная комбинация 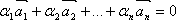при не равных нулю одновременно 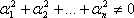. Если же только при a_i = 0 выполняется 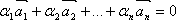, то векторы называются линейно независимыми.

1. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы.

2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.

3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.

4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.

5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.

6. Любые 4 вектора линейно зависимы.

13. Скалярное произведение векторов, его cв=ва . евклидово пространство.

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними.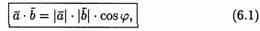

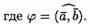
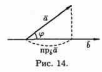
скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

Свойства :

1. 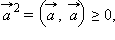причем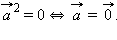

2. 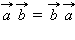переместительный закон

3. 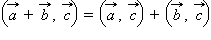распределительный закон

4. 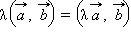сочетательный закон

Векторное пространство, в котором определено скалярное произведение, называется евклидовым пространством.

Прямая на плоскости. Ур-е прямой с угловым коэффициентом. Ур-е прямой, проход через данную точку, в заданном направлении. Ур-е прямой, проход через 2 данные точки.

0 ≤α≤π 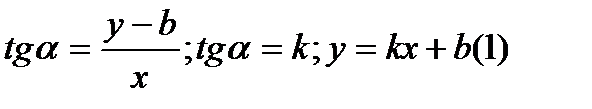-ур-ие прямой с угловым коэффиц. Подставим 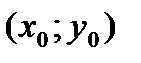в (1); 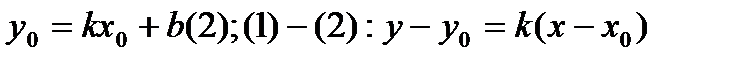(3)-ур-ие пр., проход. ч/з задан(.) с зад. угловым коэффициентом

;

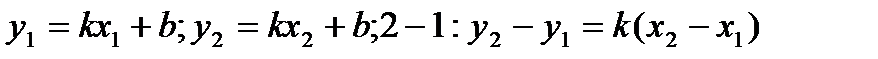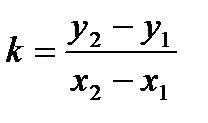, подст. в ур (3) : 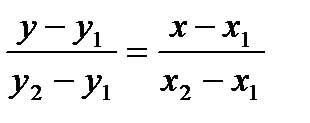- ур-ие прямой ч/з 2 данные точки.

Угол между прямыми. Условия параллельности и перпендикулярности двух прямых.

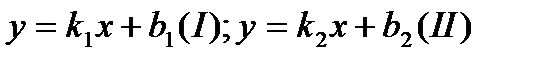
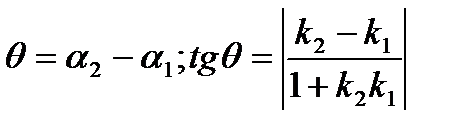
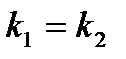-условие паралл-ти прямых;

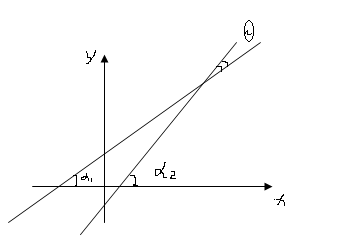
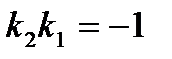-усл. перпендик-ти прямых

Если заданы две прямые y = k1x + b1, y = k2x + b2, то острый угол между этими прямыми будет определяться как .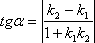

Если задана точка М(х0, у0), то расстояние до прямой Ах + Ву + С =0 определяется как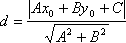

Уравнение прямой в отрезках. Общее уравнение прямой на плоскости.

Вектор n = (А; В) - нормальный вектор прямой.

В векторном виде: n*r + С = 0, где - радиус-вектор произвольной точки на прямой.

Частные случаи:

1) By + C = 0 - прямая параллельна оси Ox;

2) Ax + C = 0 - прямая параллельна оси Oy;

3) Ax + By = 0 - прямая проходит через начало координат;

4) y = 0 - ось Ox;

5) x = 0 - ось Oy.

Уравнение прямой в отрезках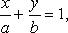

где a, b - величины отрезков, отсекаемых прямой на осях координат.

общее уравнение прямой на плоскости Ах+Ву+С=0:

Ву=-Ах-С (А,В,С не равно 0)

У=(-А/В)*х-С/В

k= -А/В=tgα

Общее уравнение плоскости.

Ax+By+Сz-Ax₀-By₀-Сz₀=0

-Ax₀-By₀-Сz₀=D, где D=Ax+By+Сz

Ax+By+Сz+D=0

Частный случай:

Если D=0, то Ax+By+Сz=0(проходит ч/з 0;0)

Если A=0, то By+Сz+D=0

Если B=0, то Ax +Сz+D=0

Если C=0, то Ax+By+D=0

Если A=B=0, то Сz+D=0

Если A=C=0, то By+D=0

Если A=D=0, то By+Сz=0

Если B=D=0, то Ay+Сz=0