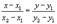Разложение вектора по ортам координатных осей.

Вектор ОА, начало которого находится в начале координат, а конец - в точке А (x1, y1, z1), называют радиус-вектором точки А и обозначают r1(A) или просто r1. Так как его координаты совпадают с координатами точки А, то его разложение по ортам имеет вид r1=x1 i+y1 j+z1 k

Вектор AB, имеющий начало в точке А(x1, y1, z1) и конец в точке B(x2, y2, z2), может быть записан в виде AB=r2-r1 где

R2 - радиус-вектор точки В;

R1- радиус-вектор точки А.

Поэтому разложение вектора по ортам имеет вид AB=(x2-x1)i+(y2-y1)j+(z2-z1)k

А=(а,б,с) |a|=корень из а в кв+б в кВ+с в кВ

А+-б=(а+б,а+б,а+б)

А||б ↔ а/б=а/б=а/б

Кос альфа=а(икс)/модуль а, кос бетта=а(у)/модуль а, кос гамма=а(з)/модуль а

Кос в кВ альфа+кос в кВ бета+ кос в кВ гамма=1

Е=(кос а, кос б, кос г)

|e|=1

I=(1,0,0)|i|=1 j(010) k(001)

AB=(x-x y-y z-z)

X=xодин+k xдва/1+k (у,з аналог)

Скалярное произведение векторов и его свойства.

Скалярное произведение векторов - число = произвед длин на косинус между ними.

Скалярное произ 2х векторов = модулю одного умноженного на проекцию другого на соноправленную с 1-ым вектором ось.

Свойства:

1. a*b=b*a

2. (C*a)*b=C*(a*b)

3. a(b+c)=a*c+b*c;

4.

5. (a, b) = 0 =>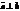

6. ij = jk = kj = 0.

Векторное произведение векторов и его свойства.

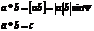
Свойства:

1.Векторное произведение по модулю равно площади параллелограмма построенного по этим векторам.

2.Вектор с являющийся векторным произведением всегда перпендикулярен к плоскости в которой лежат вектора а в .

3.Вектор с направлен так, что кратчайший поворот от а к b, наблюдаемый с конца с должен происходить против часовой стрелки.

4.Не коммутативность a*b= -b*a

5.Векторное произведение равно 0 если один из векторов =0 или они коллинеарные. 6.Ассоциативность по отношению к умножению на скаляр.

7.Дистрибутивность по отношению сложению векторов a*(b+c)=a*b+a*c.

Векторное произведение в координатной форме.

i j k

a*b=xa ya za

xb yb zb

Смешанное произведение векторов.

Смешанное произведение 3х векторов равно объёму параллелепипеда, построенного на этих векторах, взятого со знаком + (-), если эти векторы образуют правую (левую) тройку.

Свойства:

1)смешанное произв не меняется при циклической перестановке его множителей.

( .

2)смешанное произв меняет знак при перемене мест любых букв любых сомножителей

3)смешанное произ ненулевых векторов =0 тога, когда они компланарны.

Смешанное произ векторов = определителю 3-его порядка, составленного из координат перемноженных векторов. Приложение. 1)определение взаимных ориентаций векторов в ространстве: если >0 ( <0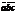), то правая (левая) тройка векторов

2)комплонарность векторов: компланарны, когда их произв =0.

3)Геометрический смысл:

Vпараллелепипеда= 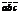. Vтр=1/6( ).

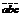Вычисление: ,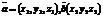

Прямая линия на плоскости.

Напомним сведения об уравнении прямой на плоскости. Любое уравнение первой степени относительно неизвестных х и у является уравнением прямой на плоскости: АX + ВY + С = 0

Оно может быть записано в некоторых специальных видах:

а) уравнение с угловым коэффициентом у= kx+b , где k - угловой коэффициент, численно равный тангенсу угла наклона прямой к положительному направлению оси Ох , а свободный член b - ордината точки пересечения графика и Оу.

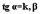-отрезок, отсекаемый графиком на оси оу

б) уравнение пучка прямых, проходящих через точку (х0 ,у0) у-у0 = k(х-х0 )

в) уравнение прямой, проходящей через две заданные точки (х1у1) и (х2у2)