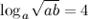Арксинус, арккосинус, арктангенс и арккотангенс на единичной окружности

Чтобы получить наглядное представление об арксинусе, арккосинусе, арктангенсе и арккотангенсе числа a, взглянем на них с позиций геометрии. Это несложно сделать, если знать про линии синусов, косинусов, тангенсов и котангенсов.

arcsin a, arccos a, arctg a и arcctg a можно связать с дугами единичной окружности, стягивающими углы, соответствующие значениям арксинуса, арккосинуса, арктангенса и арккотангенса числа a.

Для примера получим дугу, соответствующую арксинусу числа a. Для этого на линии синусов отметим точку, отвечающую числу a, после чего из нее проведем луч, параллельно и в положительном направлении оси абсцисс. Этот луч будет пересекать единичную окружность в некоторой точке. Дуга единичной окружности от этой точки до начальной точки с координатами(1, 0) и будет отвечать арксинусу числа a.

По схожим принципам можно получить дуги, отвечающие арккосинусу, арктангенсу и арккотангенсу числа a. На рисунке ниже синими линиями показаны дуги, отвечающие арккосинусу, арктангенсу и арккотангенсу числа a.

4) Показатели функции, ее свойства и график.

В практике часто используются функции y=2x,y=10x,y=(12)x,y=(0,1)x и т. д., т. е. функция вида y=ax, где a - заданное число, x - переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени - заданное число.

Функция, заданная формулойy=ax(гдеa>0,a≠1), называется показательной функцией с основаниемa.

Сформулируем основные свойства показательной функции:

1. Область определения - множество R действительных чисел.

2. Область значений - множество R+ всех положительных действительных чисел.

3. При a>1 функция возрастает на всей числовой прямой; при 0<a<1 функция убывает на множестве R.

ax1<ax2, если x1<x2,(a>1),

ax1>ax2, если x1<x2,(0<a<1)

4. При любых действительных значениях x и y справедливы равенства

axay=ax+yaxay=ax−y(ab)x=axbx(ab)x=axbx(ax)y=axy

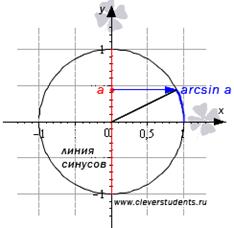
Графики показательных функций изображены на рисунках:

1) для случая a>1

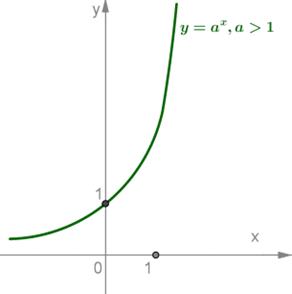
2) для случая 0<a<1

Логарифм и его свойства. Примеры

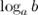Логарифмом числа по основанию ( ) называется такое число , что 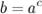, то есть запис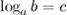и и 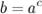равносильны. Логарифм имеет смысл, если .

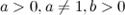Если немного перефразировать - Логарифм числа по основанию определяется как показатель степени, в которую надо возвести число , чтобы получить число (Логарифм существует только у положительных чисел).

Логарифм в переводе с греческого буквально означает "число, изменяющее отношение".

Специальные обозначения:

• Натуральный логарифм 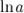- логарифм по основанию , где - число Эйлера.

• Десятичный логарифм 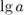- логарифм по основанию 10.

Свойства логарифмов:

1° 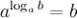- основное логарифмическое тождество.

2°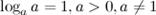

3°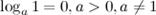

Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1 только возведя его в нулевую степень.

4° 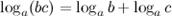- логарифм произведения.

Логарифм произведения равен сумме логарифмов сомножителей.

5° 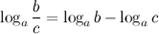- логарифм частного.

Логарифм частного (дроби) равен разности логарифмов сомножителей.

6° 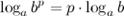- логарифм степени.

Логарифм степени равен произведению показателя степени на логарифм ее основания.

7°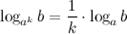

8°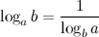

9° 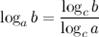- переход к новому основанию.

Вычислить 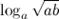, если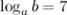

Решение. Перепишем данное выражение, используя свойство логарифма степени и логарифма произведения:

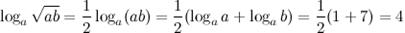
Ответ.