Вычисление длины дуги кривой.

Длина ломаной линии, которая соответствует дуге, может быть найдена как .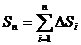

Тогда длина дуги равна .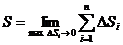

Из геометрических соображений: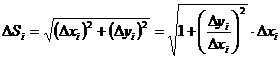

Т.е.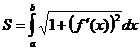

Если уравнение кривой задано параметрически, то с учетом правил вычисления производной параметрически заданной функции, получаем

, где х = j(t) и у = y(t).

Если задана пространственная кривая, и х = j(t), у = y(t) и z = Z(t), то Если кривая задана в полярных координатах, то , r = f(j) Вычисление объемов тел: Пусть имеется тело объема V. Площадь любого поперечного сечения тела Q, известна как непрерывная функция Q = Q(x). Разобьем тело на “слои” поперечными сечениями, проходящими через точки х_i разбиения отрезка [a, b]. Т.к. на каком- либо промежуточном отрезке разбиения [x_i-1, x_i] функция Q(x) непрерывна, то принимает на нем наибольшее и наименьшее значения. Обозначим их соответственно M_i и m_i.

Если на этих наибольшем и наименьшем сечениях построить цилиндры с образующими, параллельными оси х, то объемы этих цилиндров будут соответственно равны M_iDx_i и m_iDx_i здесь Dx_i = x_i - x_i-1.

Произведя такие построения для всех отрезков разбиения, получим цилиндры, объемы которых равны соответственно и .При стремлении к нулю шага разбиения l, эти суммы имеют общий предел: Таким образом, объем тела может быть найден по формуле:

11. Несобственные интеграллы первого и второго рода.Определение , примеры ,признаки сходимости.Несоб инт, т. е. опред ин от непрер ф., но с беск пром интег или опред инт с конеч промеж интег, но от ф., имющ. на нем беск разрыв. Инт с беск пром интегр (нес инт I рода) Пусть ƒ(х) непр на пром [а;+∞). Если сущ конеч предел то его назыв несобст интегралом 1 родаи обозначают Таким образом, по определению В этом случае говорят, что несоб интеграл 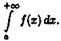схо-ся. Если же указанный предел не сущ или он бесконечен,то говорят, что интеграл расх-ся. Аналогичноопределяется несобственный интеграл на промежутке (-∞; b]:

Примеры:

1. 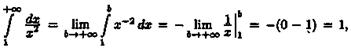сход

2. расх Признаки:

1.Сравнения : Если на промежутке [а; +∞) непрерывные функции ƒ(х) и φ(х) удовлетворяют условию 0 ≤ ƒ(х) ≤ φ(х), то из сходимости следует сходимость

а из расходимости интеграла следует расх

2. Если существует предел и φ(х) > 0), то интегралы одновременно оба сходятся или оба расходятся

Интеграл от разрывной функции (несобственный интеграл II рода)

Пусть функция ƒ(х) непрерывна на промежутке [а; b) и имеет бесконечный разрыв при х = b. Если существует конечный предел то его называют несобственным интегралом второго рода и обозначают Таким образом,поопределению

Если предел в правой части существует, то несобственный интеграл сходится. Если же указанный предел не существует или бесконечен,то говорят, что интеграл расходится.

Пример: Решение: При х = 0 функция терпит бесконечный разрыв;

Признаки сходимости для 2-го рода: 1. Сравнение : Пусть на [а; b) ƒ(х) и φ(х) непр, при х = b терпят беско разрыв и удовлет условию 0 ≤ ƒ(х) ≤ φ(x). Как в в 1-ом роде только промеж интегр от a до b 2. Пусть ƒ(х) и φ(х) непр на [а; b) и в т. х = b терпят разрыв. Если существует предел то одновременно сходятся или одновременно расходятся.

12. Определение ф.м.п. Область определения ф.м.п. Предел и непрерывность ф.м.п. Точки и линии разрыва.