Алгоритм расчета систем методом перемещений
Расчет статически неопределимых систем методом перемещений выполняется в следующей последовательности:
1. Находим степень кинематической неопределимости заданной системы.
2. Выбираем основную систему.
3. Записываем канонические уравнения метода перемещений.
4. Строим единичные и грузовые эпюры изгибающих моментов для основной системы.
5. Определяем коэффициенты и свободные члены системы канонических уравнений.
6. Проверяем правильность вычисления коэффициентов и свободных членов системы канонических уравнений.
7. Вычисляем значения неизвестных метода перемещений.
8. Строим эпюры N, Q, M для заданной системы.
9. Проверяем правильность построения окончательных эпюр.
Методы вычисления коэффициентов и свободных членов канонических уравнений
В методе перемещений для вычисления коэффициентов и свободных членов канонических уравнений используются два способа: статический и способ интегрирования эпюр.
При статическом способе реактивные усилия во введенных связях определяют из уравнений равновесия отдельных узлов рамы или ее отсеченной части.
Коэффициенты и свободные члены, представляющие собой реактивные моменты во введенных заделках, определяются вырезанием узлов и составлением уравнений вида:
(4.8)
Коэффициенты и свободные члены, представляющие собой реактивные усилия во введенных стержнях, определяются с помощью разреза элементов рамы и составления уравнений равновесия сил, действующих на отсеченную часть:
(4.9)
причем, направление оси L выбирается так, чтобы уравнение получилось наиболее простым. Вычисленное реактивное усилие считается положительным, если его направление совпадает с направлением (соответственно, угловым или линейным) перемещения связи.
Способ интегрирования эпюр целесообразно применять при расчете рам с наклонными элементами. По этому способу коэффициенты при неизвестных определяют путем интегрирования (перемножения по правилу Верещагина) соответствующих единичных эпюр:
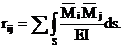(4.10)
Свободные члены канонических уравнений вычисляются в виде:
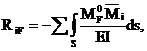(4.11)
где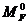 
- эпюра моментов от нагрузки, построенная в любой статически определимой системе, образованной из заданной.
Проверки метода перемещений
Так же как и в методе сил, в методе перемещений можно выполнять статическую и кинематическую проверки. Но поскольку основная система метода перемещений кинематически определима, то кинематическая проверка является вспомогательной и выполняется всегда при правильных эпюрах изгибающих моментов в основной системе и при выполненной статической проверке.
Основной проверкой в методе перемещений является проверка равновесия узлов и других частей рамы. Количество проверяемых условий равновесия должно быть не меньше числа неизвестных метода перемещений.
Проверка правильности вычисления коэффициентов при неизвестных системы канонических уравнений метода перемещений выполняется аналогично проверке коэффициентов уравнений при расчете статически неопределимых систем методом сил. Для этого строится суммарная единичная эпюра моментов 
.
Умножая эту эпюру последовательно на каждую из единичных эпюр, получим сумму коэффициентов при неизвестных в соответствующем уравнении; так, умножая эпюру 
на эпюру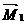 
, получим:
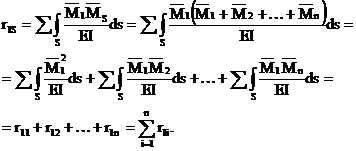
Аналогично,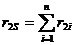 
и т.д.
Сумма коэффициентов при неизвестных i-го уравнения должна равняться значению ris, где
(4.12)
Таким образом, проверка вычисленных значений коэффициентов, входящих в первое каноническое уравнение метода перемещений, состоит в проверке условия:
(4.13)
Аналогично проверяются и коэффициенты всех остальных уравнений. Как и в методе сил, такая проверка называется построчной.
Чаще используется универсальная проверка, которая состоит в том, что результат умножения эпюры на саму себя должен равняться сумме всех коэффициентов при неизвестных системы канонических уравнений. Действительно,
(4.14)
Для проверки свободных членов канонических уравнений необходимо суммарную единичную эпюру моментов умножить на эпюру 
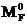, построенную от внешней нагрузки в статически определимой системе, полученной из заданной системы или основной системы метода перемещений устранением лишних связей, в том числе обязательно тех связей, реакции в которых определяются:
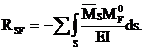(4.15)
Результат перемножения (4.15) должен равняться сумме всех свободных членов канонических уравнений:
(4.16)
Достаточной проверкой правильности окончательной эпюры моментов являются, как уже отмечалось, статические проверки, суть которых будет подробно рассмотрена ниже на конкретных примерах.
Можно также выполнить дополнительную кинематическую проверку подобно тому, как это делается в методе сил. Для этого необходимо построить единичные эпюры в основной системе метода сил и перемножить их или суммарную единичную эпюру с окончательной эпюрой изгибающих моментов. При правильном расчете результат такого перемножения должен быть равен нулю. Эта проверка служит контролем правильности принятых для расчета единичных эпюр и грузовой эпюры изгибающих моментов.