Каноническое уравнение метода перемещений

Представим уравнение (4.3) в развернутой форме. Для этого рассмотрим конкретную систему (рис.54,а). Ее степень кинематической неопределимости 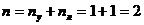, где n_у – число неизвестных углов поворота узлов; n_л – число неизвестных линейных перемещений узлов. Основную систему метода перемещений получим, вводя две дополнительных связи, одна из которых препятствует угловому перемещению узла, а другая – линейному (рис.54,б). Во введенных связях появляются реактивные усилия: момент – в заделке и сила – в стержне. Уравнения, аналогичные уравнениям (4.3), в данном случае имеют вид:

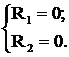(4.4)

Заменим реактивный момент R₁ суммой:

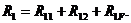
Второй индекс у обозначений реакций указывает на то воздействие, которое является причиной появления реакции, т.е. R_1F – реактивный момент во введенной заделке от действия внешней нагрузки (рис.54,в); R₁₁ – реактивный момент во введенной заделке от поворота этой же заделки на угол Z₁; R₁₂ – реактивный момент во введенной заделке от линейного смещения узлов 1 и 2 на величину Z₂.

Реактивные моменты R₁₁ и R₁₂ от Z₁ и Z₂ можно заменить выражениями:

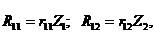
где r₁₁ – реактивный момент в заделке от поворота этой же заделки на угол 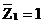(т.е. 1 радиан); r₁₂ – реактивный момент во веденной заделке от смещения по горизонтали узла на величину 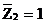(рис.54,г,д).

После этой замены первое из уравнений (4.4) получим в виде:

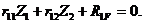(4.5)

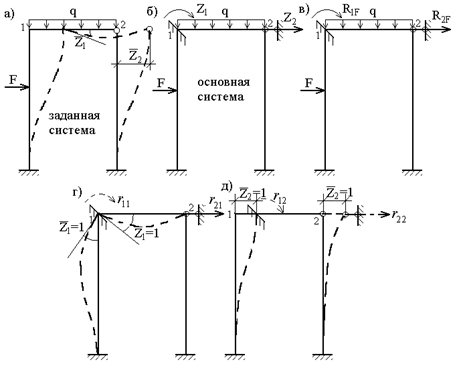
Рис. 54

Производя аналогичное преобразование второго уравнения (4.4), приведем его к виду:

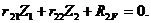
В уравнении (4.6) r₂₁ – реактивное усилие во введенном стержне, возникающее от поворота заделки на угол 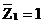(рис.54,г); r₂₂ – реактивное усилие в стержне от линейного смещения узлов 1 и 2 на величину 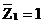(рис.54,д); R_2F – реактивное усилие в стержне от действия заданной нагрузки (рис.54,в).

Физический смысл первого уравнения состоит в отрицании момента во введенной заделке, а второго – в отрицании усилия во введенном стержне. Вместе эти уравнения образуют систему канонических уравнений метода перемещений для дважды кинематически неопределимой системы. В общем случае, при n неизвестных, система канонических уравнений метода перемещений имеет вид:

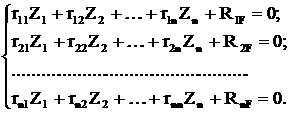(4.7)

В уравнениях (4.7) коэффициенты (реакции) 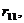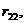…, 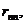расположеные на главной диагонали, называются главными; коэффициенты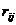 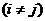называются побочными, а свободные члены R_1F, R_2F, …, R_nF – грузовыми реакциями. В этих уравнениях, так же как и в уравнениях метода сил, коэффициенты при неизвестных, расположеные симметрично относительно главной диагонали, равны друг другу:

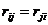
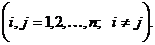
Система канонических уравнений метода перемещений отличается от аналогичной системы уравнений метода сил тем, что вместо коэффициентов 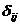и 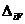, выражающих перемещения в основной системе метода сил, в нее входят коэффициенты 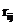и 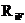, выражающие реакции дополнительных закреплений в основной системе метода перемещений, а вместо неизвестных усилий 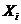- неизвестные перемещения .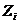