Скалярное поле: поверхности уровня, производная по направлению, градиент (оператор «набла»).
Определение: Пусть D некоторое подмножество пространства 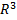 . Говорят, что на множестве D задано скалярное (векторное) поле, если с каждой точной M
. Говорят, что на множестве D задано скалярное (векторное) поле, если с каждой точной M 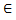 D связана некоторая скалярная (векторная) величина.
D связана некоторая скалярная (векторная) величина.
Примером скалярного поля может служить поле температуры или электрического потенциала, а примером векторного поля – поле скоростей или силовое поле.
Геометрической характеристикой скалярного поля служат так называемые поверхности уровня, т.е. геометрическое место точек, в которых данное скалярное поле или функция u=f(x,y,z) принимает одно и то же значение. Поверхность уровня определяется уравнением f(x,y,z)=C, где C=const.
В случае поля температуры, создаваемого в однородной и изотропной среде точечным источником тепла, поверхности уровня будут сферами с центром в тепловом источнике. В случае бесконечной равномерно нагретой нити поверхностями уровня будут круговые цилиндры, ось которых совпадает с нитью.
Для изучения свойств скалярного поля U=U(x,y,z) прежде всего бывает необходимо выяснить, как меняется это поле при переходе от одной точки к другой. Полное приращение будет иметь вид:
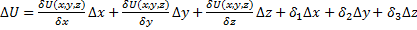 , где
, где 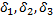 стремятся к нулю, если
стремятся к нулю, если 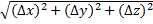 также стремится к нулю.
также стремится к нулю.
Производной функции по направлению l называется 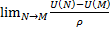 , обозначается как
, обозначается как 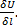
Градиентом скалярного поля называется вектор gradU= 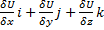 . Градиент скалярного поля перпендикулярен к поверхности уровня в каждой точке.
. Градиент скалярного поля перпендикулярен к поверхности уровня в каждой точке.
6. Криволинейный интеграл 2-го рода, случай полного дифференциала.
Криволинейным интегралом 2го рода от непрерывного векторного поля F(r) вдоль гладкой кривой L называют число:
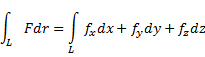
Физический смысл: криволинейный интеграл является работой по перемещению материальной точки из начало кривой в ее конец в поле силы F.
7. Векторное поле, его поток (поверхностный интеграл 2го рода), случай замкнутой поверхности: формула Остроградского-Гаусса, дивергенция векторного поля.
Пусть (S) – гладкая поверхность в трехмерном пространстве. Поверхность называется двусторонней, если нормаль к поверхности при обходе по любому замкнутому контуру, лежащему на поверхности (S) и не имеющему общих точек с ее границей, возвращается в первоначальное положение. Если это условие выполняется не для всех замкнутых контуров, то такая поверхность называется односторонней. Если выбрано направление нормали к двусторонней поверхности (одно из двух возможных), то поверхность называется ориентированной.
Предположим, что (S) – ориентированная плоскость на которой задана непрерывная функция f(x,y,z). Тогда, если существует предел 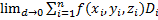 независимо от способа разложения поверхности (S) на части, то этот предел называется поверхностным интегралом 2го рода от функции f(x,y,z) и обозначается
независимо от способа разложения поверхности (S) на части, то этот предел называется поверхностным интегралом 2го рода от функции f(x,y,z) и обозначается 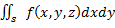 .
.
Обозначим через G трехмерное тело, ограниченное кусочно-непрерывной, гладкой замкнутой поверхностью. Предположим что задано векторное поле F(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z)).
Согласно формуле Остроградского-Гаусса 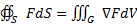 , где
, где 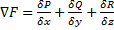 =divF.
=divF.
Учитывая это, можно переписать формулу Остроградского-Гаусса в виде
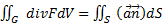 .
.
Формула Остроградского-Гаусса означает, что поток векторного поля через замкнутую поверхность (S) в направлении внешней нормали равен тройному интегралу от дивергенции этого поля по объему (V), ограниченному данной поверхностью.
