Найти точки разрыва следующих функций и определить их тип.

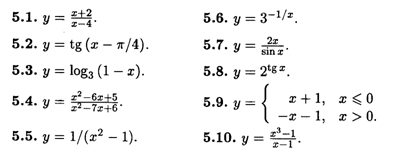
Найти производные функций.

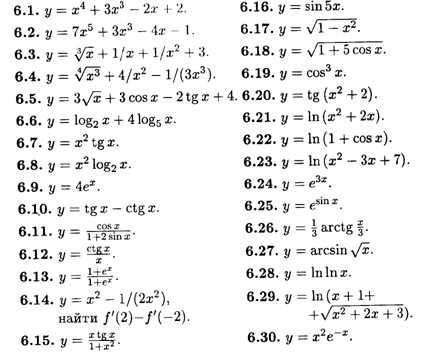
Составить уравнения касательных к графикам функций.

8. Найти производные высших порядков от следу­ющих функций.

А) Производные второго порядка

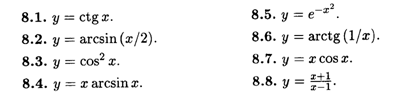
Б) Производные третьего порядка

В) Производные n-го порядка

Найти пределы с использованием

А) правила Лопиталя:

Б) разложения по формуле Маклорена:

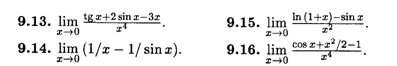
Исследовать и построить графики функций.

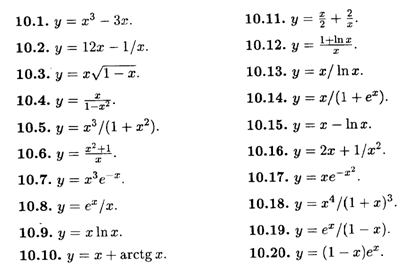
Найти неопределенные интегралы

а) непосредственным интегрированием:

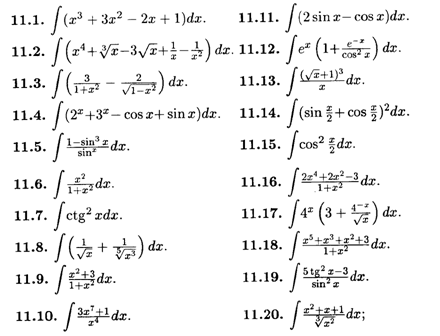
б) методом подстановки:

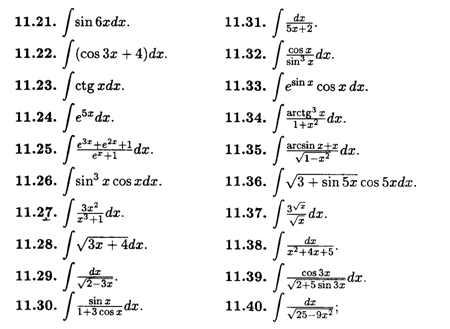
в) интегрированием по частям:

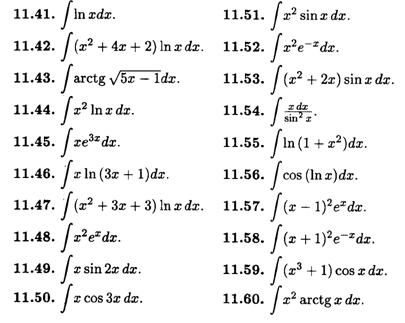
Решить задачи с определенными интегралами.

Вычислить интегралы.

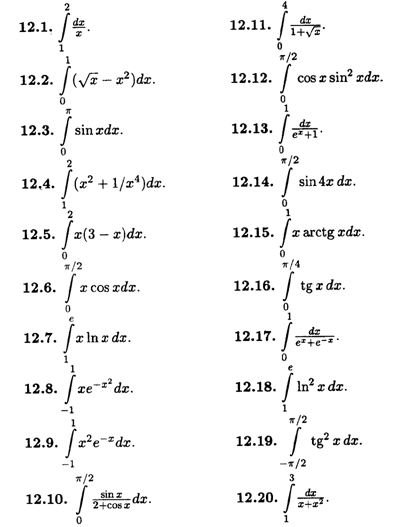
2) Найти площади фигур, ограниченных следующи­ми линиями.

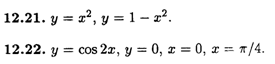
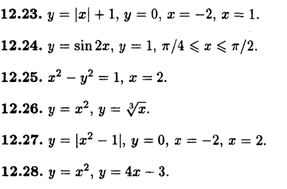
12.29. Фигура ограничена параболой у = x² + 4x — 3 и каса­тельными к ней в точках а (0, -3), b(3, 0).

12.30. Фигура ограничена параболой у = x² — 2x + 2, касатель­ной к ней в точке (3, 5) и осью Оу.

3) Найти объемы тел, образованных вращением во­круг оси Оу фигуры, ограниченной следующими лини­ями.

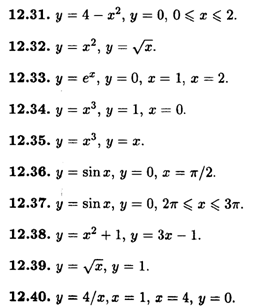
Вычислить несобственные интегралы.

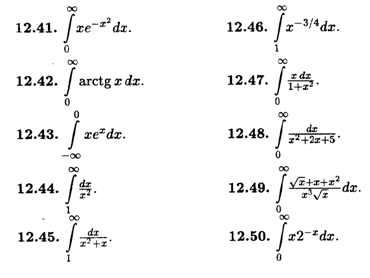
П2. Задания по теме "Математический анализ, функции нескольких переменных"

1. Найти области определения следующих функций.

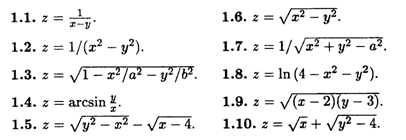
Построить линии уровня следующих функций.

Найти частные производные от функций.

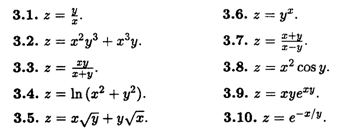
Найти градиенты функций в следующих точках.

Найти частные производные второго порядка от функций.

Найти экстремумы функций.

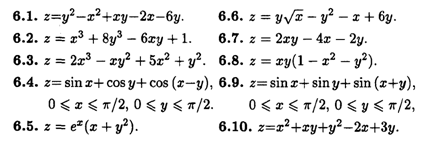
П3. Задания по теме "Обыкновенные дифференциальные уравнения"

1. Найти общие решения уравнений первого поряд­ка методом разделения переменных.

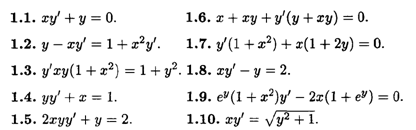
2. Найти частные решения уравнений первого по­рядка, удовлетворяющие следующим начальным усло­виям.

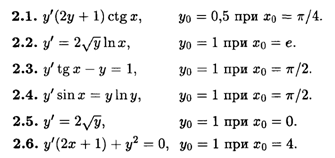
3. Найти общие решения линейных уравнений пер­вого порядка.

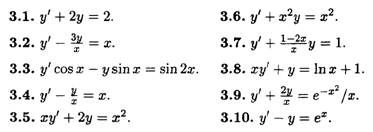
Решить уравнения Бернулли.

Найти решения линейных однородных уравнений второго порядка.

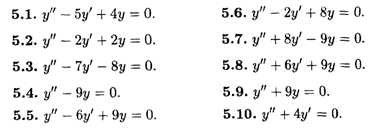
6. Решить линейные неоднородные уравнения вто­рого порядка.

7. Найти частные решения линейных уравнений второго порядка, удовлетворяющие указанным началь­ным и краевым условиям.

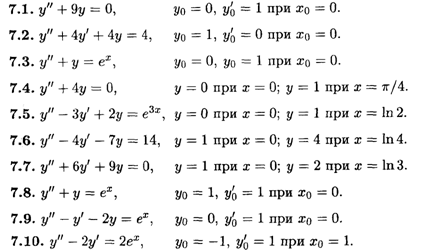
П4. Задания по теме "Элементы линейной алгебры"

Вычислить

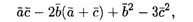
где , 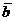и 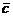— векторы, заданные в таблице.

Найти следующие комбинации этих матриц.

2.1. Матрицу H = 3С - 4F.

2.2. Соответствующие транспонированные матрицы.

2.3. Все возможные произведения матриц, имеющие смысл.

2.4. Матрицу Н = С² - F².

2.5. Матрицу Н = G³.

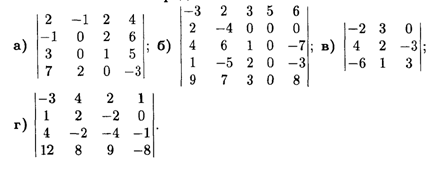
3. Вычислить определители:

4. Определить, являются ли векторы а, b и с ли­нейно независимыми. Варианты задания этих векто­ров указаны в таблице задания 1.

Найти ранги матриц, указанных в задании 2.

Решить методом Крамера системы линейных уравнений.

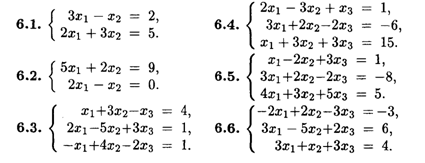
Решить задачи 6.1-6.6 методом обратной матрицы, вычислив ее методом Гаусса.

8. Решить методом Гаусса системы линейных уравне­ний 6.3-6.6.

9. Решить методом Гаусса системы линейных уравне­ний.

10. Найти фундаментальные системы решений сис­тем однородных уравнений.

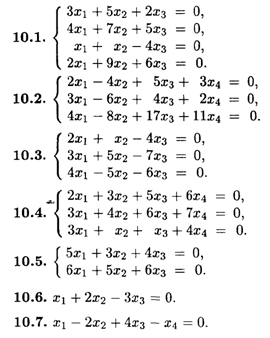
11. Найти собственные значения и собственные век­торы матриц.

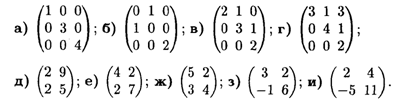
П5. Задания по теме "Элементы теории вероятностей"

Задачи на случайные события

1.1. Два нумизмата обмениваются коллекционными монетами. Найти число способов обмена, если первый нумизмат обмени­вает 5 монет, а второй — 8 монет.

1.2. В ящике находится 12 деталей, среди которых имеются 3 нестандартные. Найти вероятность того, что 3 взятые наугад детали будут стандартными.

1.3. В урне находится 20 шаров: 15 белых и 5 красных. Из урны извлекают один шар, затем, не возвращая его обратно, извлекают второй. Найти вероятность появления красного ша­ра при втором извлечении.

1.4. Абонент забыл последнюю цифру телефонного номера. Найти вероятность того, что при наборе номера наугад он на­берет его правильно не более чем с четырех попыток.

1.5. В лотерее разыгрывается 150 вещевых и 50 денежных вы­игрышей на каждые 5000 билетов. Найти вероятность выиг­рыша вообще.

1.6. В ящике находится 12 деталей, из которых 3 нестандарт­ные. Из ящика последовательно, одну за другой, берут две де­тали. Найти вероятность того, что обе детали будут стандарт­ными.

1.7. В цеху находятся четыре однотипных станка. Вероятнос­ти исправного состояния этих станков соответственно равны 0,7, 0,9, 0,8 и 0,6. Найти вероятность того, что все станки на­ходятся в эксплуатации.

1.8. На станции «Скорой помощи» дежурят две машины. Веро­ятности технической исправности машин равны соответствен­но 0,95 и 0,75. Найти вероятность исполнения поступившего вызова второй машиной.

1.9. Инвестиционный фонд вкладывает поровну средства в пять предприятий при условии возврата ему каждым пред­приятием через определенный срок 125% от вложенной суммы. Вероятность банкротства каждого из предприятий равна 0,3. Найти вероятность того, что по истечении срока кредита фонд получит обратно не менее вложенной суммы.

1.10. Таможенный досмотр автомашин осуществляют два ин­спектора. В среднем из каждых 100 машин 45 проходит через первого инспектора. Вероятность того, что при досмотре ма­шина, соответствующая таможенным правилам, не будет за­держана, составляет 0,95 у первого инспектора и 0,85 у второ­го. Машина, соответствующая таможенным правилам, не была задержана. Найти вероятность того, что она прошла досмотр у первого инспектора.

1.11. В первой коробке находится 10 шаров, из которых 4 си­них; во второй коробке — 5 шаров, из которых 3 синих. Из первой коробки наугад перекладывают один шар во вторую коробку. Найти вероятность извлечения из второй коробки си­него шара.

1.12. Три орудия произвели залп по цели, и два снаряда пора­зили ее. Найти вероятность поражения цели при залпе вторым орудием, если вероятности поражения цели орудиями равны соответственно 0,5, 0,6 и 0,7.

1.13. Найти вероятность поражения цели при залповой стрель­бе отделением из 5 солдат, если вероятность попадания в цель каждым солдатом составляет 0,5.

1.14. Из урны, содержащей белые и черные шары, извлекают по одному шару 4 раза. Найти вероятность появления белого шара:а) менее трех раз;б) не менее трех раз.

1.15. Вероятность выпуска стандартного изделия равна 0,9. Найти вероятность того, что среди 100 приобретенных изделий будет ровно 80 стандартных.

1.16. Вероятность обращения в банк клиента за возвратом де­позита равна 0,3. Найти вероятность того, что из 100 клиентов, посетивших банк, ровно 30 потребуют возврата депозита.

1.17. Вероятность появления брака в каждом из 2500 изделий равна 0,2. Найти вероятность появления стандартных изделий в количестве: а) не менее 1250; б) не менее 1200 и не более 1250; в) не более 1249. Выпуск каждого изделия полагать не­зависимым событием.

1.18. Вероятность обращения в травматологический пункт для каждого рабочего на стройке составляет 0,3. Найти, среди какого количества строителей следует ожидать обращения в пункт не менее 50 человек.

1.19. Банк выдал кредиты размером 400 тыс. р. каждому из 2000 клиентов на год под 15% годовых. Вероятность невозвра­та кредита каждым из клиентов составляет 0,05. Какой доход гарантирован банку с вероятностью: а) 0,7; б) 0,95 ?

1.20. Вероятность появления события в каждом из 1200 неза­висимых испытаний равна 0,6. Найти вероятность отклонения относительной частоты появления события от его вероятности не более чем на 2% по абсолютной величине.