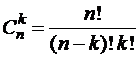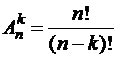Сочетания с повторениями (с возвратом)

Сочетание с повторениями из п элементов по 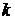элементов – результат последовательного выбора 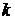объектов из совокупности, состоящей из п объектов, при котором выбираемый предмет каждый раз после фиксирования возвращается обратно, а порядок появления объектов несущественен. Если в исходном п-элементном множестве имеются одинаковые элементы, то мы также имеем сочетания с повторениями.

Число сочетаний с повторением из п элементов по 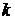дается формулой:

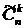
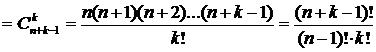
(без доказательства).

Пример 1.Бросают 4 игральные кости и записывают результат. Здесь не принимается во внимание порядок, в котором выпадают цифры. Например, если выпали по порядку 6,6,4,1, а в другой раз – 6,1,6,4, то считают, что эти результаты одинаковы. Фактически здесь имеются сочетания с повторением из 6 элементов (цифр) по 4. Их общее число, т.е. общее число всех возможных результатов, равно

= .

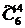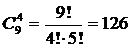Заметим, что число сочетаний без повторений с такими же индексами значительно меньше: 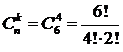=15. Это число выпадений только с различными цифрами.

Пример 2. Количество костей домино в наборе можно рассматривать как число сочетаний из семи цифр (от 0 до 6) по две с повторениями:

Обобщение

Для лучшего понимания перестановок, размещений и сочетаний можно использовать схему:

Все ли элементы множества мы выбираем?

Сочетания

Важен ли порядок расположения элементов в подмножестве?

Размещения

Нет

Да

Нет

Да

СХЕМА КОМБИНАТОРИКИ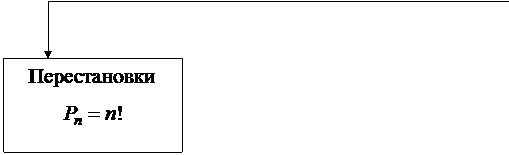

Тема: Случайные события

2. Случайные события

Испытания и события

Испытанием называется осуществление на практике какого-либо комплекса условий. В теории вероятностей изучаются только такие испытания, которые могут быть повторены, хотя бы теоретически, неограниченное число раз. В результате испытания наблюдают различные явления, которые называются событиями.

События делятся на детерминированные и случайные. Детерминированными событиями называются те, которые при неоднократном повторении испытания протекают каждый раз одинаково. Случайнымисобытиями называются события, которые могут произойти или не произойти в результате испытания по не зависящим от нас причинам.

Результатом каждого испытания является определённый исход- случайное событие, которое называется элементарным событием. В результате каждого испытания происходит одно и только одно элементарное событие. Элементарные события обычно обозначают строчными буквами w или е.

Пример 2.1.1.Подбрасывается монета (ее всегда будем считать круглой и однородной, а бросать её будем на твердую горизонтальную поверхность). В результате испытания могут быть следующие исходы: выпадение герба (орла) е_г и выпадение решки (нарицательной стоимости монеты) е_р. При математическом описании данного испытания естественно отвлечься от ряда несущественных исходов (монета встала на ребро, навсегда исчезла из вида, и т.д.) и ограничиться только двумя.

Пример 2.1.2.Испытание состоит в подбрасывании игральной кости. Предполагается, что выполнен следующий комплекс условий: игральная кость правильная, т.е. плотность вещества, из которого она сделана, постоянна, а её форма является идеальным кубом; на каждой грани этого куба написано одно и только одно из натуральных чисел от 1 до 6, кубик бросается на ровную гладкую поверхность. Эту первичную совокупность условий принято считать само собой разумеющейся, и никак не отмечать ее наличие. Элементарным событием является выпадение определённого числа очков от 1 до 6. Очевидно, что это событие является случайным.

Пример 2.1.3. Испытание состоит в вынимании одной карты из колоды. Комплекс условий: колода полная (36 или 52 карты), в ней 4 масти, и т.д. Элементарное событие – появление при этом определённой карты, например, дамы пик. Это случайное событие. Однако при раздаче карт шулером появление туза может оказаться не случайным, а детерминированным событием.

Виды случайных событий

Случайные события обозначаются заглавными буквами латинского алфавита: А, В, С, и т.д. Поскольку в дальнейшем мы будем иметь дело только со случайными событиями, вместо словосочетания «случайное событие» мы будем говорить просто «событие».

Невозможным называется событие, которое никогда не произойдёт в результате испытания. Обозначается Æ.

Пример 1.Выпадение числа 8 при бросании игральной кости.

Достоверным называется событие, которое обязательно произойдёт в результате испытания. Обозначается W.

Пример 2.Выпадение натурального числа при бросании игральной кости. Выпадение целого числа от 1 до 6 при бросании игральной кости.

Пример 3. Выбранное наугад трёхзначное число не больше 1000.

Два события называются несовместными, если наступление одного из них исключает наступление другого. Аналогично, п событий 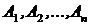называются попарно несовместными, если наступление одного из них исключает наступление любого другого.

Если наступление одного события не исключает наступление другого, то такие события называются совместными.

Пример 4. Если при единичном бросании игральной кости через 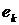обозначить событие, заключающееся в выпадении числа очков, равного 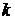, то события 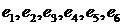будут попарно несовместными.

Пример 5.Событие А- выпадение на игральной кости числа очков, меньшего 5. Событие В – выпадение числа очков, большего 3. События А и В- совместны, т.к. выпадение четвёрки соответствует описанию обоих событий.

Пример 6. А- появление бубны при вынимании карты из колоды; В- появление трефы; С- пики; D -червы. События A, B, C, D попарно несовместны.

Пример 7.Выпадение чётного или нечётного числа очков при бросании кубика - несовместные события.