Гидравлические характеристики трубопроводов

Гидравлической характеристикой трубопровода называется зависимость напора, который необходимо создать в трубопроводе для пропуска по нему определенного расхода, т.е. Н=f(Q).

Рассмотрим некоторые особенности этой характеристики.

1. Представим себе горизонтальный трубопровод длиной l и диаметром d, питаемый, например, от насоса с постоянным расходом Q (рис.6.2).

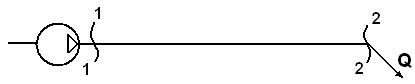
рис. 6.2

Составив уравнение Бернулли для сечений 1-1 и 2-2, получим, что напор в сечении 1-1 тратится на преодоление линейных потерь h_л.п, т.е. Н = h_л.п.. тогда формулу (6.2) представим в виде

. (6.3)

Обозначим 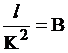. Для конкретного трубопровода это будет постоянная величина, тогда выражение (6.3) примет вид

. (6.4)

Такая явно квадратичная зависимость свойственна только турбулентному режиму движения (рис.6.3).

рис. 6.3

Из рис. 6.3 видно, что, например, для пропуска расхода Q_i в трубопроводе необходимо создать напор Н_i.

2. Допустим, что насос подает жидкость в трубопровод с преодолением статического напора Н_ст (рис.6.4).

рис. 6.4

Сначала характеристика совпадает с линией ОН (ординатой). Дальнейшее увеличение напора расходуется на преодоление гидравлических сопротивлений h_п, которые увеличиваются с увеличением расхода Q. Таким образом, аналитическое выражение такой характеристики будет иметь вид

. (6.5)

3. мы имеем, например, семейство характеристик 1,2,3 (рис.6.5). Простой анализ позволяет сделать вывод, что они принадлежат трубопроводам различного диаметра, т.е. d₁>d₂>d₃. Таким образом, например, трубопровод 1 может пропустить больший расход при меньшем напоре, чем трубопроводы 2 и 3.

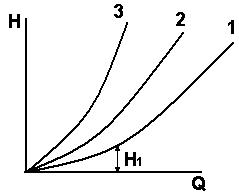
Рис. 6.5 Рис. 6.6

4. Гидравлическую характеристику трубопровода определенного диаметра можно изменить, например, с помощью задвижки. В выражении Н=ВQ² изменяется коэффициент В. Задвижкой в этом случае вводится дополнительное сопротивление, эквивалентное определенной длине трубопровода (рис.6.6).

5. Примем, что насос подает жидкость в трубопровод с верхнего бака в нижний (рис.6.7), т.е. имеет место «отрицательного» статического напора. В этом случае напор Н` без насоса обеспечит расход в трубопроводе Q`. Для увеличения расхода подключается насос.

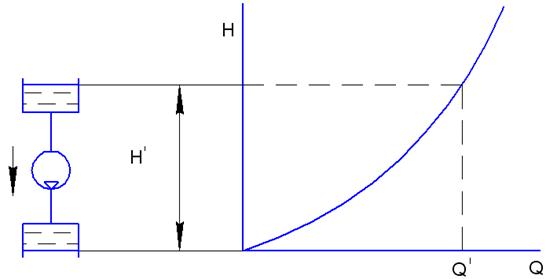
Рис. 6.7

6. гидравлическая сеть состоит из нескольких трубопроводов различного диаметра и длины, соединенных последовательно (рис.6.8).

Рис. 6.8

Очевидно, что ; ;

. (6.6)

Суммарную характеристику можно получить по выражению (6.6) или построением характеристик отдельных ее участков 1,2 и 3 с последующим графическим их сложением (рис.6.9).

Рис. 6.9

7. гидравлическая сеть состоит из нескольких трубопроводов различного диаметра и длины, соединенных параллельно (рис. 6.10).

Рис. 6.10

Очевидно, что . В точках А и В напор одинаков для трубопровода с расходом Q₁ и Q₂. следовательно, падение напора в каждой ветке одинаково, т.е. Н=Н₁=Н₂ или

. (6.7)

Суммарную характеристику получают построением характеристик отдельных ее участков с последующим графическим их сложением (рис.6.11).

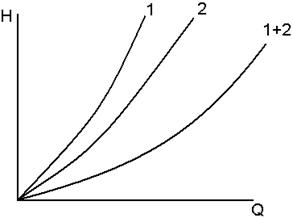
Рис. 6.11

Равномерный путевой расход

Во многих случаях приходится рассчитывать устройства, в которых жидкость расходуется равномерно по длине трубопровода. Это дождевальные и моечные устройства. Кроме того, например, уличный трубопровод системы водоснабжения несмотря на неравномерность расхода по его длине, рассчитывается как трубопровод с равномерным расходом.

Равномерный путевой расход характеризуется интенсивностью .

В общем случае, кроме путевого расхода, данный участок l пропускает некоторый транзитный расход Q_т (рис. 6.12).

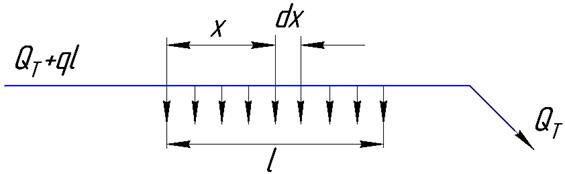
Рис.6.12

Общий расход в начальном сечении участка Q = Q_T+ql.

Определим линейные потери напора на участке l. Для этого рассмотрим сначала элемент участка dx, расположенный на расстоянии х от начала.

Через рассматриваемый элемент dx проходит весь транзитный расход Q_т, а также та часть путевого расхода, которая следует на участке l-х:

.

Для определения линейных потерь на участке l воспользуемся формулой , представив ее в виде

.

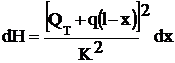Тогда потери напора на участке l

. (6.8)

Выражение (6.8) легко интегрируется для квадратичной зоны графика Никурадзе. В этом случае K = сonst. Имея в виду, что Q_n=ql, получим:

. (6.9)

В том случае, если транзитный расход Q_т отсутствует, получаем:

. (6.10)

Таким образом, при отсутствии транзитного расхода равномерный расход эквивалентен расходу, сосредоточенному на конце участка:

.