Закон Архимеда. Основы теории плавания
Применим описанный выше прием нахождения вертикальной составляющей силы давления жидкости на криволинейную поверхность для доказательства известного закона Архимеда.
Предположим, что в жидкость погружено тело АВСД, ограниченное любой криволинейной поверхностью (рис.3.17). Проектируя тело на вертикальную плоскость и пользуясь формулой (3.23) нетрудно понять, что горизонтальные силы давления слева и справа уравновешиваются, поскольку площадь проекции одна и та же, т.е. 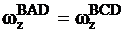 , тогда
, тогда 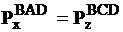
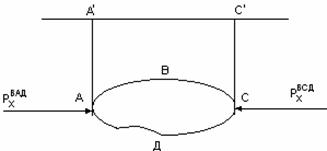
Рис.3.17
Для определения вертикальной силы давления на погруженное тело рассмотрим отдельно вертикальные составляющие на нижнюю поверхность АДС и верхнюю АВС.
Вертикальная составляющая силы избыточного давления жидкости на верхнюю часть поверхности тела 
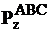 направлена вниз и равна весу жидкости в объеме АА′С′СВА.
направлена вниз и равна весу жидкости в объеме АА′С′СВА.
Вертикальная составляющая силы давления жидкости на нижнюю часть поверхности тела 
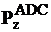 направлена вверх и равна весу жидкости в объеме АА′С′СДА.
направлена вверх и равна весу жидкости в объеме АА′С′СДА.
Отсюда следует, что вертикальная равнодействующая силы давления жидкости на тело будет направлена вверх, она равна весу жидкости в объеме, равном разности указанных двух объемов, т.е. в объеме тела:
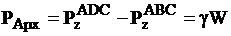 . (3.27)
. (3.27)
В этом и заключается закон Архимеда, обычно формулируемый так: на тело, погруженное в жидкость, действует выталкивающая сила, равная весу вытесненной этим телом жидкости.
На законе Архимеда основана теория плавания тел, в которой в качестве первых задач определяются плавучесть и остойчивость.
Плавучестью тела называется его способность плавать в полупогруженном состоянии.
В зависимости от соотношения между весом плавающего тела G и подъемной силой Рп возможны три состояния тела, погруженного в жидкость. Подъемная сила при этом приложена в центре погруженной части тела, называемом центром водоизмещения.
1. G>Рп – тело тонет.
2. G<Рп – тело плавает в полупогруженном состоянии.
3. G=Рп – тело в погруженном состоянии.
В первом случае тело тонет, т.к. равнодействующая сила G и Рп направлена вниз.
Во втором случае равнодействующая сил G и Рп направлена вверх, поэтому тело всплывает. Однако оно поднимается над поверхностью воды лишь до тех пор, пока новая подъемная сила Рп не будет равна весу тела, т.е. G=Рп.
В третьем случае, когда первоначально G=Рп (довольно редкий случай), тело может находиться в устойчивом, неустойчивом или безразличном равновесии.
При воздействии на плавающее тело внешних сил, например ветра, навала судов, оно будет отклоняться от положения равновесия (давать крен).
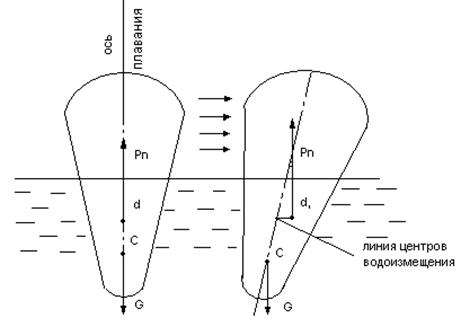
Рис.3.18
Каждое плавающее тело должно обладать остойчивостью. При этом различают остойчивость статическую и динамическую. Рассмотрим только статическую остойчивость.
Под статической остойчивостью подразумевают способность плавающего тела плавать в нормальном положении и в случае статического нарушения нормального положения вследствие крена возвращаться в прежнее положение, как только силы, вызвавшие крен, прекратят свое действие.
При исследовании остойчивости необходимо иметь в виду, что при крене плавающего тела (судна) его центр тяжести является всегда одной и той же точкой С (рис.3.18). центр же водоизмещения (точка d) вследствие того, что изменяется форма объема вытесненной телом жидкости, перемещается по линии, называемой линией центров водоизмещения, поэтому при крене плавающего тела сила тяжести и равная ей по величине подъемная сила всегда создают пару сил. Для того чтобы тело обладало статической остойчивостью, необходимо, чтобы эта пара сил стремилась возвратить тело в нормальное положение. Это, например, будет иметь место во всех случаях, когда центр тяжести расположен ниже центра водоизмещения. Но в большинстве случаев центр тяжести находится выше центра водоизмещения (рис.3.19, 3.20).
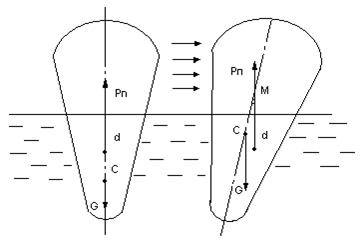
Рис.3.19
Здесь могут представиться два случая. Первый случай – остойчивое плавание (рис.3.19). При крене плавсредства по часовой стрелке центр водоизмещения располагается правее линии действия силы тяжести. В этом случае линия действия подъемной силы Рп пересекает ось плавания в точке М, расположенной выше центра тяжести. Создающаяся при этом пара сил (Р-G) стремится возвратить плавсредство в исходное состояние.
Второй случай – неостойчивое плавание (рис.3.20). При крене плавсредства по часовой стрелке центр водоизмещения располагается левее линии действия силы тяжести. В этом случае линия действия подъемной силы Рп пересекает ось плавания в точке М, расположенной ниже центра тяжести. Создающаяся при этом пара сил (P-G) стремится опрокинуть плавсредство.
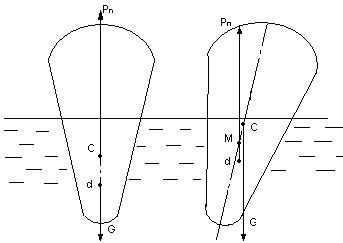
Рис.3.20
Точка М пересечения линии действия подъемной силы с осью плавания называется метацентром.
Для того чтобы тело обладало остойчивостью, необходимо, чтобы метацентр находился выше центра тяжести.
