Занятие 6. Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции

В качестве числовых характеристик системы случайных величин выступают математические ожидания и дисперсии составляющих системы. Для системы используют корреляционный момент k_xy и безразмерную величину - коэффициент корреляции r_xy:

Зная плотности распределения составляющих X и Y

непрерывной двумерной случайной величины (X,Y), можно найти их математические ожидания и дисперсии

М[X]= М[Y]=

D[X]=

D[Y]=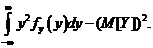

,

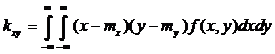r_xy = ,

где 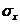= 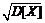и 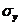= 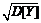- средние квадратические отклонения случайных величин X и Y.

Иногда удобнее использовать формулы

М[X]= 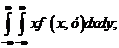М[Y]=

D[X]=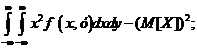

D[Y]=

.

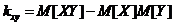Корреляционный момент характеризует рассеивание случайных величин X и Y. Если величины X и Y независимы, то корреляционный момент равен нулю. Обратное утверждение неверно, если 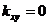, то система (X,Y) может быть зависимой. Это значит, что равенство нулю корреляционного момента является необходимым, но не достаточным условием независимости случайных величин.

Пример 6.1. Рассмотрим вновь двумерное распределение

Найти корреляционный момент.

Решение. Воспользуемся результатами, полученными в примере 5. Было показано, что , т.е. случайные величины X и Y - зависимые.

Чтобы найти корреляционный момент надо знать m_x и m_y

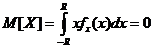и , т.к. функции f_х(x) и f_у(y) - четные.

Получили, что корреляционный момент равен нулю, а случайные величины зависимые.

­ Пример 6.2.Плотностьвероятности двумерной случайной величины (Х,Y) задана формулой

f(x,у)=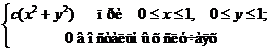

1. Найти параметр С.

2. Найти .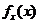

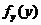3. Вычислить: , , , ,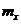

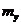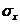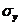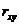
4. Выяснить, зависимы или нет Х, У.

1. Коэффициент С находим из условия

Отсюда С=3/2.

2. Применяем известные формулы

=

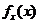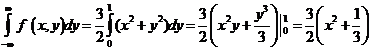
при x 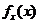=0 при х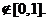 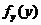записываем из условия равноправности вхождения переменных х, у в выражение для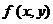

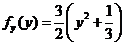при y 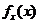=0 при y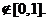

3. Находим .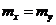

=

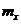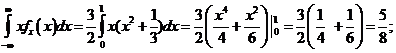
Аналогично 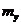=5/8.

Находим 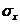= 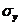. Предварительно найдем М[ ]и D_x:

М[ ]=

D_x= М[ ]- =

=

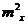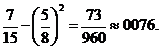
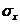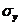
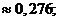
Найдем 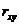. Предварительно найдем М[ 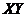]и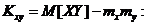

М[ ]=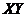

5. Так как 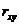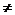0, то Х, Y зависимы.

Задачи для самостоятельного решения

1. Вычислить математические ожидания составляющих системы двух случайных величин, заданной плотностью вероятностей:

f(x,у)=

2. Двумерная случайная величина задана таблицей

Y	Х
0,5	0,1	0,3	0,25
1,5	0,15	0,15	0,05

Найти математические ожидания составляющих и корреляционный момент.

3. Задана двумерная плотность вероятностей системы случайных величин (Х,Y)

f(x,у)=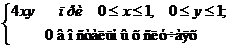

Найти математические ожидания и дисперсии составляющих и корреляционный момент.

4.Задана функция распределения двумерной случайной величины

Найти математические ожидания составляющих.

Ответы: 1. m_x=m_y=π/4. 2.m_x=4,1; m_y=0,85; 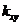=-0,235.

3.m_x=m_y=2/3,D(X)= D(Y)=1/18, 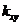=0.4.m_x=m_y=(π-2)/4

Задачи для типовых расчетов

Задача 1. Дискретная случайная величина Х может принимать только два значения: х₁ и х₂, причем х₁<х₂. Известны вероятность р₁ возможного значения х₁, математическое ожидание М[X] и дисперсия D[X]. Найти закон распределения этой

случайной величины

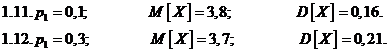
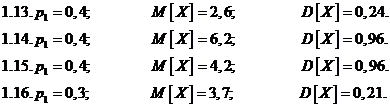
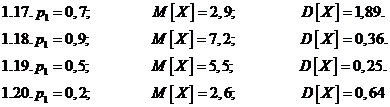
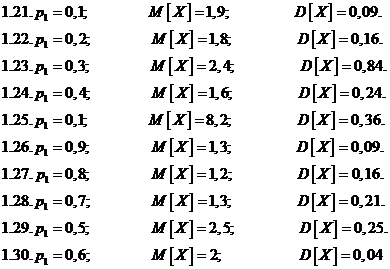
Задача 2.Дана плотность распределения f(x) случайной величины Х. Найти параметр а, функцию распределения случайной величины, математическое ожидание М[Х], дисперсию D[X], вероятность выполнения неравенства х₁<x< x₂, построить график функции распределения F(x) . (См. исходные данные)

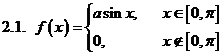
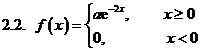
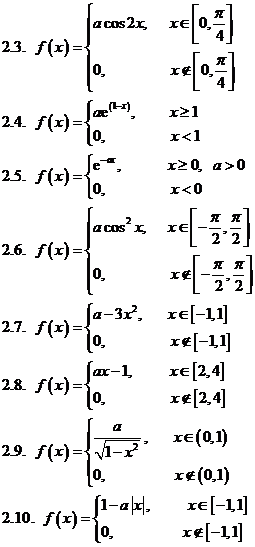
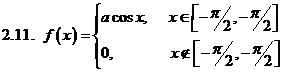
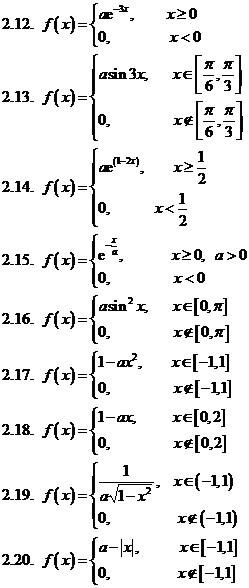
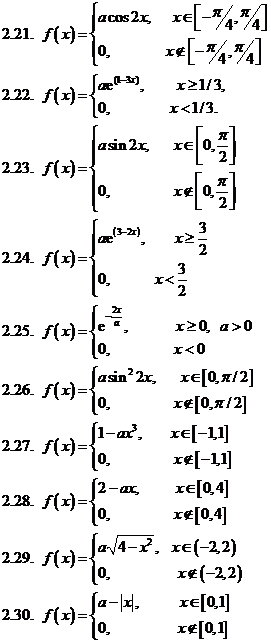
Задача 3. Дана плотность распределения p(x) случайной величины ξ. Найти параметр γ, математическое ожидание Мξ, дисперсию Dξ, функцию распределения случайной величины ξ, вероятность выполнения неравенства x₁<ξ<x₂. (См. исходные данные.)

Варианты 1-8: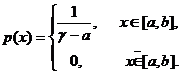

Варианты 9-16: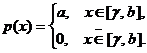

Варианты 17-24: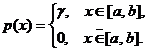

Варианты 25-31: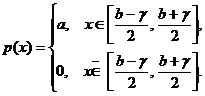

Задача 4.Плотность распределения вероятностей случайной величины ξ имеет вид 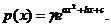Найти: γ, математическое ожидание Мξ, дисперсию Dξ, функцию распределения случайной величины ξ, вероятность выполнения неравенства x₁<ξ<x₂. (См. исходные данные.)

Задача 5. Найти вероятность попадания в заданный интервал (α,β) нормально распределенной случайной величины, если известны ее математическое ожидание а и среднее квадратическое отклонение σ (См. исходные данные в таблице).

Задача 6. Детали на производстве сортируются на 4 группы по величине отклонений от номиналов двух существенных параметров. Отклонения ранжируются. Ранги Х, У отклонений могут принимать лишь значения 0 и 1. Распределение двумерной случайной величины (Х,У) задано таблицей (См. исходные данные)

X \ Y

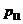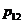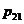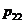Найти коэффициент корреляции 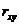называемый paнгoвым.

Задача 7. Двумерная случайная величина (Х, У) распределена равномерно в области D.

1. Составить плотность вероятности).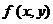

2. Найти .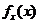

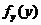3. Вычислить: , , , , .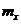

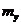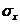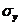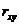4. Выяснить, зависимы или нет Х и У.

1. D − четверть кpyгa: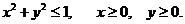

2. D − треугольник с вершинами 0(0, 0), А(1,0), В(0, 1).

3. D − четверть эллипса: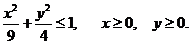

4. D − четверть эллипса: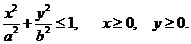

5. D − треугольник с вершинами А(1,0), В(1, 1), С(0, 1).

6. D − треyгольник с вершинами 0(0, 0), А(-1,0), В(0, -1).

7. D − полукруг: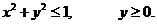

8. D − кpуг: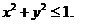

9. D − полукруг: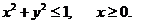

10. D − треугольник с вершинами А(-1,0), В(0, 1), С(1,0),

11. D − криволинейный треугольник, ограниченный линиями

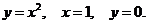
12. D − криволинейный треугольник, ограниченный линиями

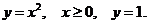
13 D − криволинейный треугольник, ограниченный линиями

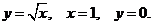
14. D − криволинейный треугольник, ограниченный линиями

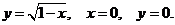
15. D − криволинейный треугольник, ограниченный линиями

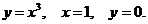
16. D − криволинейный треугольник, ограниченный линиями

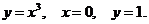
17. D − криволинейный треугольник, ограниченный линиями

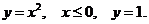
18. D −− криволинейный треугольник, ограниченный линиями

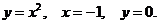
19. D − полукруг: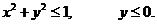

20. D − полукруг: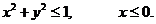

21. D − трапеция с вершинами А(0,0), В(0, 1), С(1, 1), D(2,0).

22. D − четверть кpyгa: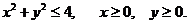

23. D − трапеция с вершинами А(0,0), В(0, -1), С(1, -1), D(2,0).

24. D − четверть кpyгa: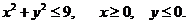

25. D − трапеция с вершинами А(2,0), В(3, 1), С(4, 1), D(4,0).

26. D − область, ограниченная линиями

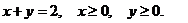
27. D − трапеция с вершинами А(0,0), В(0, 2), С(2, 2), D(4,0).

28. D − область, ограниченная линиями

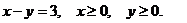
29. D − трапеция с вершинами А(0,0), В(0, -2), С(2, -2), D(4,0).

30. D − область, ограниченная линиями

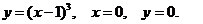
Задача 8. Дана плотность вероятности f(х,у). двумерной случайной величины (Х, У)

1. Найти значение параметра с .

2. Найти: .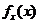

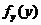3. Вычислить: , , , ,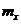

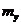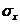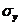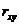
4. Выяснить, зависимы или нет Х, У.

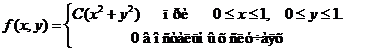
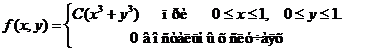
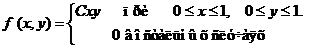
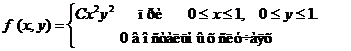
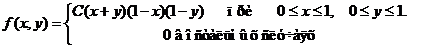
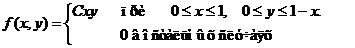
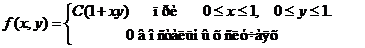
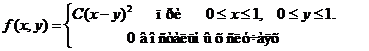
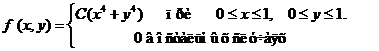
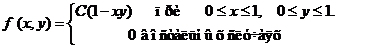
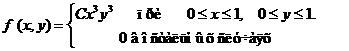
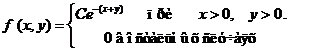
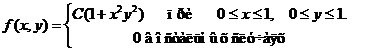
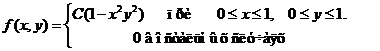
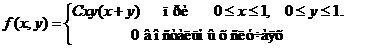
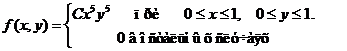
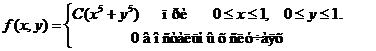
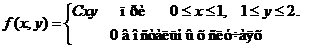
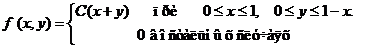
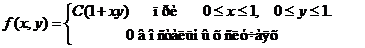
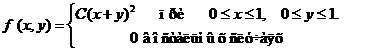
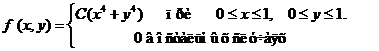
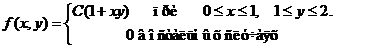
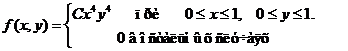
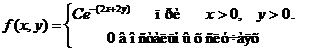
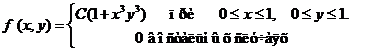
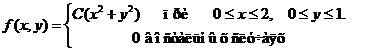
Исходные данные к расчетным заданиям

Вариант	Задача 2	Задача 3
х1	х2	a	β	x1	x2
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21.	-2 π/6 -1 -π/6 -1 -1 -1 π/6 -1 -π/8 π/8 -1	π/2 π π π/4 π/2 π/3 π/8 π/4 π/4 1/2	2,5 1,5 1,5 -1 -2 -3 -1,5 -4 -3 -1 -1,5 -1,5 0,5 0,2 0,5 0,4 ¼ 0,02	2,5 3,5 2,5 1,8 2,4 3,5 2,8 2,8 2,6 4,8 -2 -1 1,5 1,5 -1	-0,7 -1,5 -2 -1 1,3 1,5 2,5 2,1 -1 1,5 4,5 -1 -2 -1 -1	3,3 2,6 2,3 2,8 1,1 0,3 1,6 2,5 0,5 0,5

Вари- ант	Задача 4
a	b	c	x1	x2
	-2 -2 -2 -4 -3 -4 -3 -3 -2 -3 -2 -2 -2 -4 -3 -4 -3 -3 -2 -3 -2 -4 -2 -4 -3 -3 -3 -3 -2 -2 -1	4/3 -8 -6 -3 -4 -4/3 4/3 -8 -6 -3 -4 -4/3 -8 -6 -4 -3 -4/3 4/3	-2 -2/3 -2 -2 2/3 -2 -1 -1 -1 -1 1/3 -1/3	1/3 -3/2 ½ -3/4 -1/2 1/3 -1/3 -1/3 1/3 -3/2 ½ -3/4 -1/2 1/3 -1/3 -1/3 -3/2 -3/4 ½ 1/3 -1/2 -1/3 -1/3 1/3 -1/3	2/3 -1 ¾ 3/2 ¼ 3/2 4/3 2/3 5/3 2/3 -1 ¾ 3/2 ¼ 3/2 4/3 2/3 5/3 ¾ -1 ¼ 3/2 4/3 3/2 5/3 2/3 2/3 4/3

Вариант	Задача 5	Задача 6
α	β	σ	a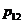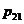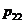
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21.					0,94 0,8 0,03 0,2 0,2 0,2 0,5 0,4 0,45 0,1 0,2 0,05 0,1 0,25 0,35 0,25 0,06 0,25 0,85 0,3 0,92 0,4 0,9 0,7 0,1 0,2 0,1 0,35 0,2 0,8	0,01 0,05 0,05 0,1 0,2 0,1 0,1 0,2 0,3 0,2 0,4 0,1 0,05 0,1 0,15 0,2 0,24 0,1 0,02 0,15 0,02 0,1 0,04 0,05 0,1 0,1 0,2 0,15 0,3 0,1	0,02 0,01 0,02 0,1 0,1 0,2 0,2 0,3 0,1 0,1 0,1 0,05 0,05 0,2 0,05 0,1 0,14 0,15 0,03 0,05 0,01 0,2 0,01 0,05 0,1 0,1 0,3 0,2 0,25 0,05	0,03 0,05 0,9 0,6 0,5 0,5 0,2 0,1 0,15 0,6 0,3 0,8 0,8 0,45 0,45 0,45 0,56 0,5 0,1 0,5 0,05 0,3 0,05 0,2 0,7 0,6 0,4 0,3 0,25 0,05

Таблица значений функции ,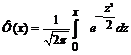

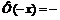
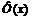
x
0,0	0,00000
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0	0,49865	3,1		3,2		3,3		3,4
3,5		3,6		3,7		3,8		3,9
4,0
4,5
5,0

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Гмурман В.Е. Теория вероятностей и математическая статистика: учеб. пособие / В.Е. Гмурман. 12-е изд. М. : Высшее образование, 2008. - 479 с.

2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие / В.Е. Гмурман. 11-е изд., перераб. М. : Высшее образование, 2007. - 404 с.

3. Пискунов Н.С. Дифференциальное и интегральное исчисления: учеб. пособие для втузов: в 2-х т. / Н.С. Пискунов. М.: Интеграл-Пресс, 2006. Т. 2.

4. Данко П.Е. Высшая математика в упражнениях и задачах: учеб. пособие для студентов втузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. М.: ООО «Издательский дом «ОНИКС 21 век»: ООО «Издательство «Мир и Образование», 2006. Ч. 2.

СОДЕРЖАНИЕ

Введение . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . 1

Занятие 1. Случайные величины. Виды случайных величин. . . . . . . . . . . . . Задание дискретной случайной величины. . . . . . . . 1

Занятие 2. Числовые характеристики дискретных случайных

величин. Функция распределения

дискретных случайных величин . . . . . . . . . . . 6

Занятие 3. Непрерывные случайные величины. Функция

распределения. Плотность распределения

вероятностей………………….. . . . . . . . . . . . . . . . .11

Занятие 4. Числовые характеристики непрерывных

случайных величин. Равномерное и нормальное

распределения непрерывных случайных величин.16

Занятие 5.Системы. случайных величин. . . . . . . . . . . . . . . . . 23

Занятие 6. Числовые характеристики системы . случайных

величин.Корреляционный момент. Коэффициент

корреляции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28

Задачи для типовых расчетов . . . . . . . . . . . . . . . . . . .. . . . . . 33

Библиографический список . . . . . . . . . . . . . . . . . . . . . . . . . . . 48

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по высшей математике по теме «Элементы

теории вероятностей. Случайные величины» для студентов специальностей 160201 “Самолето-

и вертолетостроение”, 130501 “Проектирование, сооружение и эксплуатация газонефтепроводов

и газонефтехранилищ” очной формы обучения

Составители:

Дурова Валентина Николаевна

Зайцева Марина Ивановна

Кузнецова Валентина Ивановна

Соколова Ольга Анатольевна

В авторской редакции

Компьютерный набор В.Н. Дуровой

Подписано в печать 08.12.2009

Формат 60x84/16. Бумага для множительных аппаратов.

Усл. печ. л. 3,1. Уч.- изд. л. 2,9. Тираж. 50 экз. “С”.

Зак. №

ГОУВПО « Воронежский государственный технический

университет»

394026 Воронеж, Московский просп., 14