РАБОТАЮЩЕГО НА КРУЧЕНИЕ (ЗАДАЧА № 10)

Условие задачи

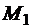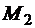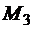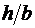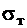Имеется стержень, расчетная схема которого представлена на рис. 3.5, а. Стержень нагружен внешними парами , , . Левый участок стержня выполнен из чугуна и имеет прямоугольное сечение с заданным соотношением сторон ; правый участок выполнен из стали и имеет круглое сечение. Известны характеристики прочности материалов: ( ) для чугуна и для стали; упругие постоянные материалов - , n; допускаемый погонный угол закручивания .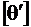

Требуется:

1) подобрать размеры поперечных сечений стержня так, чтобы выполнялись условия прочности и жесткости на каждом участке стержня;

2) построить эпюру изменения угла закручивания по длине стержня.

Решение

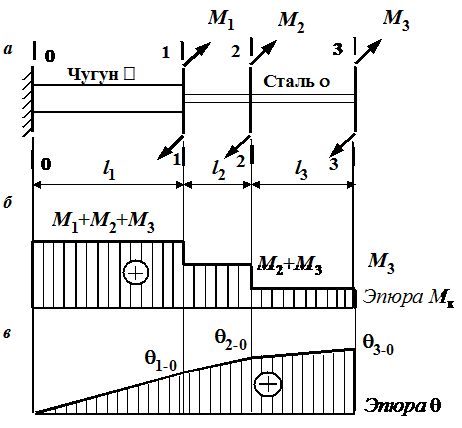Рис. 3.5. К решению задачи № 10: а – расчетная схема стержня; б, в – эпюры крутящих моментов и углов закручивания

Строим эпюру крутящих моментов, используя метод сечений. Крутящий момент на каждом участке находим как алгебраическую сумму моментов внешних пар, расположенных справа от сечения. (В этом случае можно построить эпюру М_к без определения реактивного момента, возникающего в защемлении.) Крутящий момент на крайнем правом участке равен 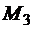, на среднем - 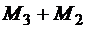и на левом - 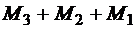. Эпюра крутящих моментов показана на рис. 3.5, б.

Подбираем размеры сечения стержня из условия прочности. На чугунном участке стержня 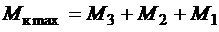и из условия прочности (3.13), определяя 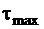по формуле (3.5), находим минимально необходимую величину момента сопротивления кручению: 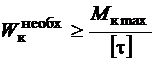и, зная 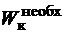, определяем ширину сечения 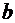из формулы (3.11): 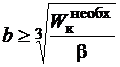. (Значение [t] высчитываем либо по второй теории прочности (3.14), либо по (3.15) – теории Мора.)

Для стального участка опасным является сечение, где действует максимальный крутящий момент, т. е. в данном примере 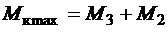, и из условия прочности (3.13) находим требуемый полярный момент сопротивления

,

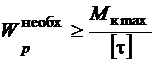где [t] определяем по теориям прочности, справедливым для пластичного материала (3.16) или (3.17). Зная 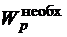, ищем радиус поперечного сечения, используя формулу (3.8) для полярного момента сопротивления

.

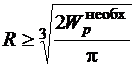Полученные размеры рекомендуем округлить в большую сторону до 0,1 мм.

Проверим, выполняется ли для найденных из условия прочности размеров поперечных сечений условие жесткости. Сосчитаем геометрические характеристик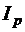и и 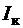по формулам (3.8) и (3.10) и модули сдвига чугуна и стали по (3.12).На чугунном участке стержня должно выполняться условие

.

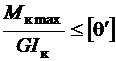На стальном участке должно быть

.

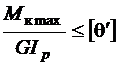Если условие жесткости на каком-то участке не выполняется, то следует увеличить размеры сечения. Из условия жесткости находим минимально необходимую геометрическую характеристику жесткости для прямоугольного сечения:

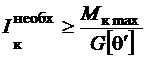
и требуемый полярный момент инерции для круглого сечения

.

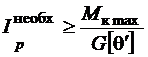Зная 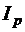и 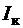, определяем по формулам (3.10) и (3.8) размеры поперечного сечения, удовлетворяющие условию жесткост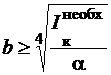и

и .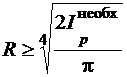

Окончательно размеры, удовлетворяющие двум условиям (и условию прочности, и условию жесткости), и соответствующие им геометрические характеристики сечений используем в дальнейших расчетах.

Построим эпюры касательных напряжений в поперечных сечениях стержня (рис. 3.2 и 3.4), сосчитав значения напряжений по формуле (3.2) для круглого сечения и по формулам (3.5) , (3.6) для прямоугольного сечения. Заметим, что по найденным значениям напряжений можно проверить свои вычисления, а именно, если размеры сечения были определены из условия прочности, то значения максимальных касательных напряжений должны быть близки к допускаемым. Если же размер сечения находился из условия жесткости, то максимальные напряжения будут меньше допускаемых касательных напряжений.

Построим эпюру углов закручивания. Углы закручивания на каждом участке стержня вычисляются по формулам (3.3) или (3.7). При этом следует учитывать знак крутящего момента. Построение эпюры углов закручивания следует начинать, определив угол закручивания q_1–0 сечения 1–1 (рис. 3,5, а) по отношению к неподвижному сечению 0–0 (заделке). Например, в рассматриваемом примере

.

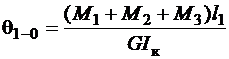Угол закручивания q_2–1 сечения 2–2 по отношению к сечению 1–1 найдем по формуле (3.3):

.

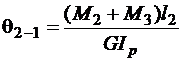Аналогично находится угол закручивания q_3–2 сечения 3–3 по отношению к сечению 2–2. На эпюре q откладываем полные углы закручивания сечений по отношению к неподвижному сечению, т. е.

, .

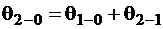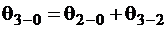Вид эпюры углов закручивания зависит от того, найдены ли размеры поперечного сечения из условия прочности или из условия жесткости. На рис. 3.5, в показан вид эпюры q, построенной в предположении, что размеры поперечных сечений найдены из условия прочности. В этом случае угол наклона эпюры q на каждом участке прямо пропорционален величине крутящего момента и обратно пропорционален жесткости стержня при кручении (GI_p, GI_к). Если размеры сечений на всех участках получены из условия жесткости, то угол наклона эпюры q на опасных участках должен быть одинаковым.