Коэффициенты регрессии. Линии регрессии.
Коэффициенты регрессии показывают интенсивность влияния факторов на результативный показатель. Если проведена предварительная стандартизация факторных показателей, то b0 равняется среднему значению результативного показателя в совокупности. Коэффициенты b1, b2, ..., bn показывают, на сколько единиц уровень результативного показателя отклоняется от своего среднего значения, если значения факторного показателя отклоняются от среднего, равного нулю, на одно стандартное отклонение. Таким образом, коэффициенты регрессии характеризуют степень значимости отдельных факторов для повышения уровня результативного показателя. Конкретные значения коэффициентов регрессии определяют по эмпирическим данным согласно методу наименьших квадратов (в результате решения систем нормальных уравнений).
Линия регрессии - линия, которая точнее всего отражает распределение экспериментальных точек на диаграмме рассеяния и крутизна наклона которой характеризует зависимость между двумя интервальными переменными.
Линия регрессии чаще всего ищется в виде линейной функции 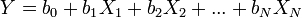 (линейная регрессия), наилучшим образом приближающей искомую кривую. Делается это с помощью метода наименьших квадратов, когда минимизируется сумма квадратов отклонений реально наблюдаемых
(линейная регрессия), наилучшим образом приближающей искомую кривую. Делается это с помощью метода наименьших квадратов, когда минимизируется сумма квадратов отклонений реально наблюдаемых 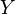 от их оценок
от их оценок 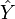 (имеются в виду оценки с помощью прямой линии, претендующей на то, чтобы представлять искомую регрессионную зависимость):
(имеются в виду оценки с помощью прямой линии, претендующей на то, чтобы представлять искомую регрессионную зависимость):
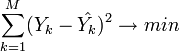
(M — объём выборки). Этот подход основан на том известном факте, что фигурирующая в приведённом выражении сумма принимает минимальное значение именно для того случая, когда 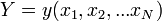 .
.
57. Основные задачи теории корреляции.
Теория корреляции представляет собой аппарат, оценивающий тесноту связей между явлениями, которые находятся не только в причинно-следственных отношениях. С помощью теории корреляции оцениваются стохастические, но не причинные связи. Автором совместно с Лукацкой М. Л. предпринята попытка получить оценки для причинных связей. Однако вопрос о причинно-следственных отношениях явлений, о том, как опознать причину и следствие, остается открытым, и кажется, что на формальном уровне он принципиально не разрешим.
Теория корреляции и ее применен к анализу производства.
Теория корреляции, являющаяся одним из разделов математической статистики, позволяет сделать обоснованные предположения о возможных пределах, в которых с известной степенью надежности будет находиться исследуемый параметр, если другие статистически связанные с ним параметры получат определенные значения.
В теории корреляции принято выделять две основные задачи.
Первая задача теории корреляции — установить форму корреляционной связи, т.е. вид функции регрессии (линейная, квадратичная и т.д.).
Вторая задача теории корреляции — оценить тесноту (силу) корреляционной связи.
Теснота корреляционной связи (зависимости) У на X оценивается по величине рассеивания значений У вокруг условного среднего. Большое рассеивание свидетельствует о слабой зависимости У от X, малое рассеивание указывает на наличие сильной зависимости.
58. Корреляционная таблица и ее числовые характеристики.
На практике в результате независимых наблюдений над величинами X и Y, как правило, имеют дело не со всей совокупностью всех возможных пар значений этих величин, а лишь с ограниченной выборкой из генеральной совокупности, причем объем n выборочной совокупности определяется как количество имеющихся в выборке пар.
Пусть величина Х в выборке принимает значения x1, x2,....xm, где количество различающихся между собой значений этой величины, причем в общем случае каждое из них в выборке может повторяться. Пусть величина Y в выборке принимает значения y1, y2,....yk, где k - количество различающихся между собой значений этой величины, причем в общем случае каждое из них в выборке также может повторяться. В этом случае данные заносят в таблицу с учетом частот встречаемости. Такую таблицу с группированными данными называют корреляционной.
Первым этапом статистической обработки результатов является составление корреляционной таблицы.
| Y\X | x1 | x2 | ... | xm | ny |
| y1 | n12 | n21 | nm1 | ny1 | |
| y2 | n22 | nm2 | ny2 | ||
| ... | |||||
| yk | n1k | n2k | nmk | nyk | |
| nx | nx1 | nx2 | nxm | n |
В первой строке основной части таблицы в порядке возрастания перечисляются все встречающиеся в выборке значения величины X. В первом столбце также в порядке возрастания перечисляются все встречающиеся в выборке значения величины Y. На пересечении соответствующих строк и столбцов указываются частоты nij (i=1,2,...,m; j=1,2,...,k) равные количеству появлений пары (xi;yi) в выборке. Например, частота n12 представляет собой количество появлений в выборке пары (x1;y1).
Так же nxi 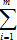 nij, 1≤i≤m, сумма элементов i-го столбца, nyj
nij, 1≤i≤m, сумма элементов i-го столбца, nyj 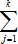 nij, 1≤j≤k, - сумма элементов j-ой строки и
nij, 1≤j≤k, - сумма элементов j-ой строки и 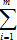 nxi=
nxi= 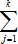 nyj=n
nyj=n
Аналоги формул , полученные по данным корреляционной таблицы, имеют вид:
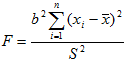
59. Эмпирическая и теоретическая линии регрессии.
Теоретическая линия регрессии может быть рассчитана в этом случае по результатам отдельных наблюдений. Для решения системы нормальных уравнений нам потребуются те же данные: х, у, ху и хг. Мы располагаем данными об объеме производства цемента и объеме основных производственных фондов в 1958 г. Ставится задача: исследовать зависимость между объемом производства цемента ( в натуральном выражении) и объемом основных фондов. [1]
Чем меньше теоретическая линия регрессии ( рассчитанная по уравнению) отклоняется от фактической ( эмпиричной), тем меньше средняя ошибка аппроксимации.
Процесс нахождения теоретической линии регрессии представляет собой выравнивание эмпирической линии регрессии на основе метода наименьших квадратов.
Процесс нахождения теоретической линии регрессии называется выравниванием эмпирической линии регрессии и заключается в выборе и обосновании типа; кривой и расчете параметров ее уравнения.
Эмпирическая регрессия строится по данным аналитической или комбинационной группировок и представляет собой зависимость групповых средних значений признака-результата от групповых средних значений признака-фактора. Графическим представлением эмпирической регрессии – ломаная линия, составленная из точек, абсциссами которых являются групповые средние значения признака-фактора, а ординатами – групповые средние значения признака-результата. Число точек равно числу групп в группировке.
Эмпирическая линия регрессии отражает основную тенденцию рассматриваемой зависимости. Если эмпирическая линия регрессии по своему виду приближается к прямой линии, то можно предположить наличие прямолинейной корреляционной связи между признаками. А если линия связи приближается к кривой, то это может быть связано с наличием криволинейной корреляционной связи.
60. Выборочные коэффициенты корреляции и регрессии.
Если зависимость между признаками на графике указывает на линейную корреляцию, рассчитывают коэффициент корреляции r, который позволяет оценить тесноту связи переменных величин, а также выяснить, какая доля изменений признака обусловлена влиянием основного признака, какая – влиянием других факторов. Коэффициент варьирует в пределах от –1 до +1. Если r=0, то связь между признаками отсутствует. Равенство r=0 говорит лишь об отсутствии линейной корреляционной зависимости, но не вообще об отсутствии корреляционной, а тем более статистической зависимости. Если r = ±1, то это означает наличие полной (функциональной) связи. При этом все наблюдаемые значения располагаются на линии регрессии, которая представляет собой прямую.
Практическая значимость коэффициента корреляции определяется его величиной, возведенной в квадрат, получившая название коэффициента детерминации.
Регрессия, аппроксимируемая (приближенно описывающаяся) линейной функцией y = kX + b. Для регрессии У на X уравнение регрессии: `y x = ryx X + b; (1). Угловой коэффициент ryx прямой регрессии Y на X называется коэффициентом регрессии Y на X.
Если уравнение (1) отыскивается по выборочным данным, то оно называется выборочным уравнением регрессии. Соответственно, ryx - выборочный коэффициент регрессии Y на X, а b - выборочный свободный член уравнения. Коэффициент регрессии измеряет вариацию Y, приходящуюся на единицу вариации X. Параметры уравнения регрессии (коэффициенты ryx и b) находятся методом наименьших квадратов.
61. Оценка значимости коэффициента корреляции и тесноты корреляционной связи в генеральной совокупности
Значимость коэффициентов корреляции проверяемся по критерию Стьюдента:
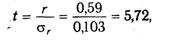
где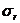 - среднеквадратическая ошибка коэффициента корреляции, которая определяется по формуле:
- среднеквадратическая ошибка коэффициента корреляции, которая определяется по формуле:
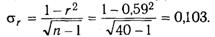
Если расчетное значение ( выше табличного, то можно сделать заключение о том, что величина коэффициента корреляции является значимой. Табличные значения t находят по таблице значений критериев Стьюдента. При этом учитываются количество степеней свободы (V = п — 1)и уровень доверительной вероятности (в экономических расчетах обычно 0,05 или 0,01). В нашем примере количество степеней свободы равно: п — 1 = 40 - 1 = 39. При уровне доверительной вероятности Р = 0,05; t = 2,02. Поскольку (фактическое во всех случаях выше t-табличного, связь между результативным и факторными показателями является надежной, а величина коэффициентов корреляции - значимой.
Оценка коэффициента корреляции, вычисленная по ограниченной выборке, практически всегда отличается от нуля. Но из этого еще не следует, что коэффициент корреляции генеральной совокупности также отличен от нуля. Требуется оценить значимость выборочной величины коэффициента или, в соответствии с постановкой задач проверки статистических гипотез, проверить гипотезу о равенстве нулю коэффициента корреляции. Если гипотеза Н0 о равенстве нулю коэффициента корреляции будет отвергнута, то выборочный коэффициент значим, а соответствующие величины связаны линейным соотношением. Если гипотеза Н0 будет принята, то оценка коэффициента не значима, и величины линейно не связаны друг с другом (если по физическим соображениям факторы могут быть связаны, то лучше говорить о том, что по имеющимся ЭД эта взаимосвязь не установлена). Проверка гипотезы о значимости оценки коэффициента корреляции требует знания распределения этой случайной величины. Распределение величины ik изучено только для частного случая, когда случайные величины Uj и Uk распределены по нормальному закону.
В качестве критерия проверки нулевой гипотезы Н0 применяют случайную величину 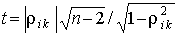 . Если модуль коэффициента корреляции относительно далек от единицы, то величина t при справедливости нулевой гипотезы распределена по закону Стьюдента с n – 2 степенями свободы. Конкурирующая гипотеза Н1 соответствует утверждению, что значение ik не равно нулю (больше или меньше нуля). Поэтому критическая область двусторонняя.
. Если модуль коэффициента корреляции относительно далек от единицы, то величина t при справедливости нулевой гипотезы распределена по закону Стьюдента с n – 2 степенями свободы. Конкурирующая гипотеза Н1 соответствует утверждению, что значение ik не равно нулю (больше или меньше нуля). Поэтому критическая область двусторонняя.
62. Вычисление выборочного коэффициента корреляции и построение выборочного уравнения прямой линии регрессии.
Выборочный коэффициент корреляциинаходится по формуле
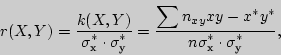
где 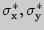 - выборочные средние квадратические отклонения величин
- выборочные средние квадратические отклонения величин 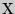 и
и 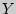 .
.
Выборочный коэффициент корреляции 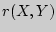 показывает тесноту линейной связи между
показывает тесноту линейной связи между 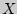 и
и 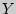 : чем ближе
: чем ближе 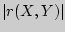 к единице, тем сильнее линейная связь между
к единице, тем сильнее линейная связь между 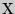 и
и 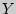 .
.
Простая линейная регрессия позволяет найти линейную зависимость между одной входной и одной выходной переменными. Для этого определяется уравнение регрессии - это модель, отражающая зависимость значений Y, зависимой величины Y от значений х, независимой переменной х и генеральной совокупности, описывается уровнением:
где А0 - свободный член уравнения регрессии;
А1 - коэффициент уравнения регрессии
Затем строится соответствующая прямая, называемая линией регрессии. Коэффициенты А0 и А1, называемые также параметрами модели, выбираются таким образом, чтобы сумма квадратов отклонений точек, соответствующих реальным наблюдениям данных, от линии регрессии, была бы минимальной. Подбор коэффициентов производится по методу наименьших квадратов. Иными словами, простая линейная регрессия описывает линейную модель, которая наилучшим образом аппроксимирует зависимость между одной входной и одной выходной переменными.
