Критерий оптимальности транспортной задачи

План перевозок

является оптимальным планом тогда и только тогда, когда найдется система платежей

для которой выполняются условия :

Доказательство. Сформулируем вторую теорему двойственности в терминах переменных транспортной задачи.

Ели

удовлетворяют ограничениям прямой задачи, а

удовлетворяют ограничениям двойственной задачи, то для оптимальности плана

необходимо и достаточно выполнение условий

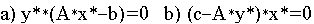
Условие а) выполняется для любых допустимых решений прямой задачи, так как

Условие b) можно расписать как следствие о дополняющей нежесткости, а именно

Итак, для базисных переменных

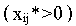
имеем равенство

а для небазисных переменных

достаточно выполнения допустимости двойственных переменных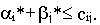

Таким образом имеем условия 1) и 2) критерия.

Критерий доказан.

9.5 Построение опорного плана транспортной задачи

Методы решения транспортной задачи сводятся к простым операциям с транспортной таблицей, которая имеет вид: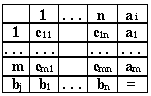

Базисными клетками транспортной таблицы являются клетки с от-

личными от нуля положительными перевозками, остальные клетки - свободные. Базисные клетки образуют опорный план транспортной задачи, если выполняются два условия:

1) сумма перевозок в каждой строке равна запасу в данной

строке;

2) сумма перевозок в каждом столбце равна соответствующему

столбцу спросу

Опорный план транспортной задачи содержит не более n+m-1

отличных от нуля перевозок

Опорный план называется вырожденным, если число ненулевых перевозок

меньше и n+m-1, опорный план - невырожден, если число

ненулевых перевозок равно n+m-1.

Рассмотрим способы построения опорного плана в невырожденном и вырожденном случаях.

Метод севево-западного угла

Рассмотрим "северо-западный угол" незаполненной таблицы, то

есть клетку, соответствующую первому поставщику и первому потребителю.

Возможны три случая.

Это означает, что первый поставщик отгрузил весь произведенный продукт первому потребителю и его

запас равен нулю, поэтому

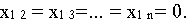
При этом неудовлетворенный спрос в первом пункте потребления равен

то есть спрос первого потребителя полностью удовлетворен и поэтому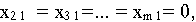

а остаток продукта в первом пункте производства равен

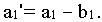
из рассмотрения можно исключить и поставщика, и потребителя. Однако при атом план получается вырожденным,

поэтому условно считается, что выбывает только поставщик,

а спрос потребителя остается неудовлетворенным и равным нулю.

После этого рассматриваем северо-западный угол оставшейся не-

заполненной части таблицы и повторяем те же действия. В результате

через n+m-1 шагов получим опорный план.

10. Математическая модель транспортной задачи. Открытые и закрытые задачи. Допустимый, опорный и оптимальный планы перевозок.

Под названием «транспортная задача» объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом. Однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.

Открытая и закрытая транспортные задачи. Выделяют два типа ТЗ: открытая ТЗ и закрытая ТЗ.

Транспортная задача называется закрытой, если выполняется условие баланса : суммарный объем производства равен суммарному объему потребления:

. (3.1)

Следнет обратить внимание на то, что математическая модель задает закрытую транспортную задачу.

Открытая ТЗ имеет место в двух случаях.

Первый случай. Суммарный объем производства меньше суммарного объема потребления:

. (3.2)

Известно, что для существования допустимого решения транспортной задачи необходимо и достаточно, чтобы задача была закрытой. Поэтому транспортную задачу открытого типа предварительно необходимо свести к закрытой, для чего вводится фиктивный пункт производства с номером m+1 с объемом производства:

, (3.3)

при этом полагают .

Второй случай. Суммарный объем производства больше суммарного объема потребления:

. (3.4)

Для сведения ТЗ к закрытому типу вводят фиктивный пункт потребления с номером n+1 с объемом потребления:

, (3.5)

при этом полагают .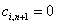

Методы решения.

· Как задача линейного программирования ТЗ может быть решена симплекс методом [4].

· Также разработаны специальные (более эффективные) методы решения транспортной задачи: обобщенный венгерский метод [4]; метод северо-западного угла, метод минимального элемента для нахождения опорного плана; метод потенциалов для нахождения оптимального плана [3].

11. Построение начального (опорного) плана перевозок по методу северо–западного угла и по методу наименьшей стоимости.

1.Метод северо-западного угла. При нахождении опорного плана на каждом шаге рассматривают первый из оставшихся пунктов отправления и первый из оставшихся пунктов назначения. Заполнение клеток таблицы условий начинается с левой верхней клетки для неизвестного («северо-западный угол») и заканчивается клеткой для неизвестного , т.е. как бы по диагонали таблицы.

2. Метод наименьшей стоимости. Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую и в клетку 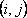, которая ей соответствует, помещают меньшее из чисел 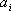и 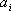, затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс размещения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.