Теорема о вероятности произведения событий.
Вероятность произведения двух событий равна произведению вероятноти одного события на словную вероятность другого при условии, что первое событие произошло:
P(AB)=P(A)*P(B/A)= P(B)*P(A/B)
P(B/A)=P(AB) / P(A)
Доказательство:
Пусть всего имеется n равновозможных исходов
n
A:l+s
AB: s
Тогда P(A)=(l+s)/n
P(B/A)=s/(l+s)
P(AB)=s/n=(l+s)s / n(l+s) = P(A)*P(B/A)
Следствие:
Вероятность приозведения n событий
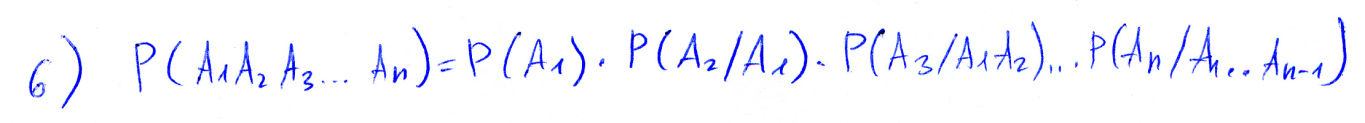
Независимые события.
О. События A и B называются независимыми, если условная вероятность события B при условии, если A произошло, равна безусловной вероятности события B:
P(B/A)=P(B)
P(AB)=P(A)*P(B/A)=P(A)*P(B)=P(AB)
Теорема
Если событие A и B независимые, то вероятность их произведения равна произведению вероятности этих событий.
О. События A1,A2,…An называются независимыми в совокупности, если они попарно независимы, а также независимы каждые из них и пересечение всех остальных n-1.
Теорема:
Если события A1, A2, … An независимы в совокупности, то вероятность их произведния равна произведению вероятности этих событий.
P(A1A2…An)=P(A1)P(A2)…P(An)
Пример
Зависимы ли события A и B, если они несовместны?
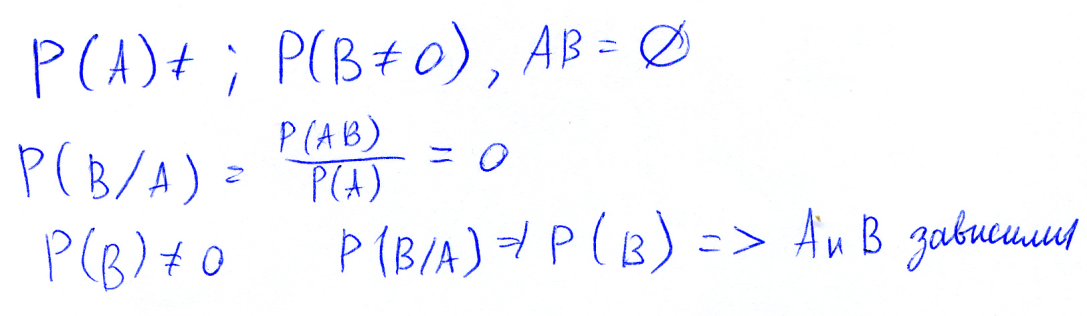
ВОПРОС № 4
Формула полной вероятности. Формулы Байеса. Априорная и апостериорная вероятности.
Пусть от первого предприятия поступило 20 изделий, от второго – 10, и от третьего – 70. Вероятности некачественного изготовления изделия на предприятиях соответственно равны 2/100 3/100 5/100
Определить вероятность получения некачественного изделия.
А: Бракованные изделия
P(A)=0,2*0,02+0,1*0,03+0,7*0,05=0,042=4,2%
Полученный процент всегда больше самого маленького и меньше самого большого.
Предположим, что в результате опыта может произойти одно из n несовместных и составляющих полную группу событий Hi. Пусть событие A может осуществиться лишь вместе с одним из событий H1, H2…Hn. Пусть также нам известны и вероятности P(H1),… P(Hn, P(A(H1)… , P(A(Hn)). Заранее не известно, с каким из событий Hi произойдет событие A, то события Hi называют гипотезами. Определим безусловную вероятность события A
Вероятности гипотез до проведения опыта называются априорными, а вероятности, вычисленные после опыта – апостериорными.
Считая, что до опыта были известны априорные вероятности P(H1),P(Hn) и условные вероятности P(A/H1)… , P(A/Hn), определим апостериорные вероятности:
Предприятие, производящее компьютеры, получает одинаковые чипы от двух поставщиков. Первый поставляет 65% чипов, второй – 35%. Известно, что качество поставляемых чипов разное. Первый – 98% качественных, второй – 95%. Предприятие осуществляет гарантийный ремонт компьютеров. Имея данные о числе компьютеров, поступающих на гарантийный ремонт всвязи с неисправностью чипов. Переоцените вероятности того, что возвращенный для ремонта компьютер укомплектован чипом от первого поставщика.
А: бракованный чип
ВОПРОС № 5
Геометрическое и статистическое определение вероятности
Геометрические вероятности – это вероятности попадания точки в область. Она пропорциональна мере данной области.
Пример
В круг, радиусом R=1 равномерно бросается точка. Найти вероятность события A, заключающегося в попадании этой точки в круг радиусом r=1/2
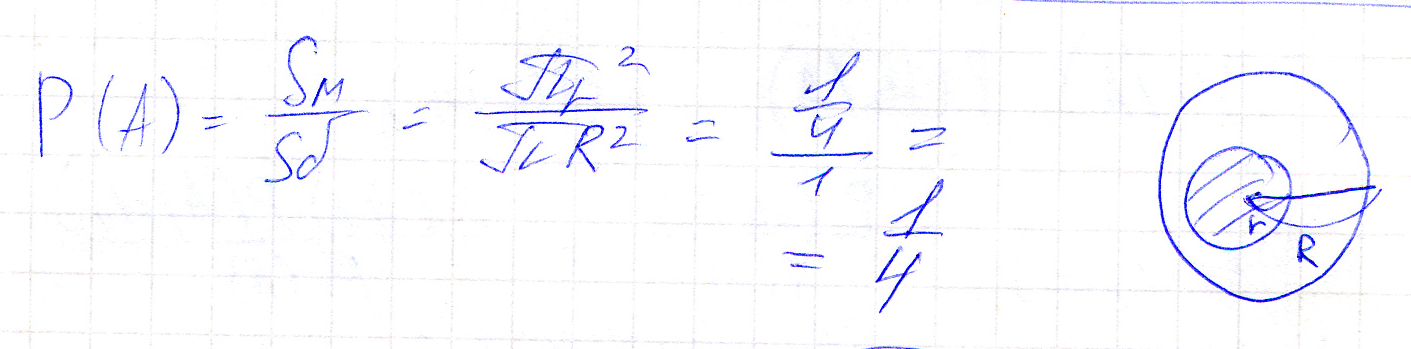Положение 1
Если все возможные событие могут быть изображены в виде точке на отрезке длиной Lобщ, а события, благоприятные событию B могут быть изображены на отрезке длиной Lb, то
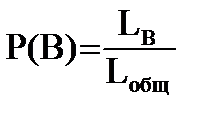
Если все возможные события могут быть изображены в виде точки на плоской фигуре площадью Sобщ, а события, благоприятные B, могут быть изображены на плоской фигуре площадью SB, то вероятность
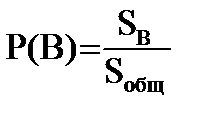
Если все возможные события могут быть изображены в виде точки в 3-х мерном пространстве внутри фигуры объёмом V общ, а события, благоприятные B в виде точки объёмом VB, то вероятность события B: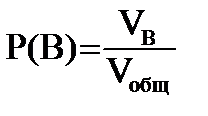 
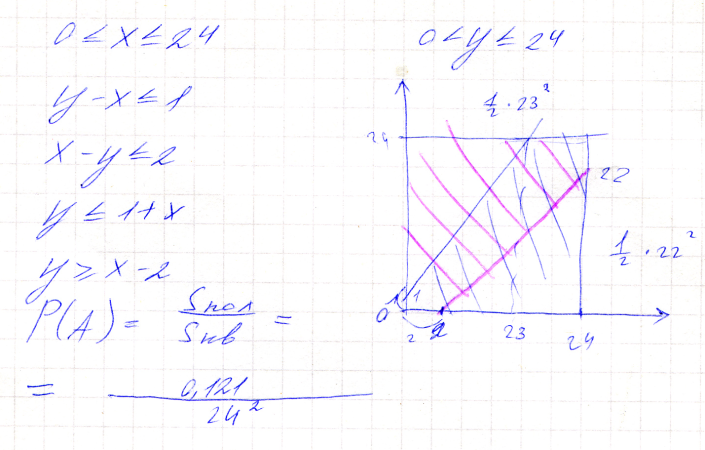
Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов независимо и равновозможно в течении данных суток. Определить вероятность того, что одному из пароходов придется ожидать освобождение причала, если время стоянки первого парохода равно 1 часу, а второго – 2 часам.
Пример
A: “Доллар дорожает”
H1 – активный эк.рост
H2 – умеренный
H3 – низкий
