Производная частного функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле

№44. Четные и нечетные функции. Периодические функции. Свойства четной функции y=│x│. Основные элементарные функции их графики.. Переменные и постоянные величины. Определение функции. Способы задания функций.

1))))) Если исследуемая функция при изменении знака аргумента значение функции не изменяется то эта функция четная, f(-x)=f(x),а если при изменении знака аргумента знак меняется то она нечетная, f(-x)=-f(x). Функция y=f(x) называется периодической, если существует такое постоянное число C, от прибавления (или вычитания) которого к аргументу x значение функции не изменяется: f(x+C)=f(x). y=│x│ (рис) f ’(0) не существует. Определенной касательной провести нельзя. x=0 –min, y(0)=0, y(x)>y(0) при 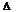x>0, при 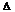x<0.

2))))) Если к каждому значению переменной «х» из некоторой области соответствует одно определенное значение «у», то это называется функция от переменной «х» у=f(х). х- независимая переменная или аргумент. Зависимость между «х и у» называется функциональной буквой «f» в символической записи функция означает, что над «х» надо произвести некоторые операции, чтобы получить «у». Совокупность значений «ч» для которых определяется значение функции «у» в силу правила f(x) называется областью определения функции. Они бывают: 1) степенная y=x^α α?R x>0. 2)показательная y=a^x a>0 x?R a≠1. 3) Тригонометрические y=sinx y=cosx y=secx и т.д. 4) Логарифмические y=log_ax a>0, a≠1, x>0. 5) Обратные тригонометрические y=arcsinx, y=arccosx, и т.д.

3))))) Переменной величиной называется величина, которая принимает различные численные значения. Величина, численные значения которой не меняются, называется постоянной величиной. В математике постоянная величина часто рассматривается как частный случай переменной, у которой все численные значения одинаковы. Если каждому значению переменной x, принадлежащему некоторой области, соответствует одно определенное значение другой переменной y, то y есть функция от x или, в символической записи, y=f(x), y=φ(x), и т.п. Способы задания функции. 1) Аналитический. 2) Графический. 3) Табличный. 4) Словесно.

№45. Определение предела функции в точке, геометрическая интерпретация.

Опр:пусть ф-ция y=f(x) определена в нек-ой окрестности точки а. число b называют пределом ф-ции f(x) при хŠ∞ если для любого числа e>0 сущ.число δ зависящее от e>0,такое,что для всех х отличных от “а”и удовлетворяющих нер-ву |х-а|<δ будет выполняться нер-во |f(x)-b|<e. y=f(x) b=lim_xŠa f(x),если для -e>0 сущ.δ(e)>0, -х≠а,|х-а|<δ,=>|f(x)-b|<e; 0<|x-a|<δ. Пусть f(x)Šb при хŠа. Т.к. из нер-ва |х-а|<δ=>|f(x)-b|<e,то это значит, что для всех х отстоящих от точки а не далее чем на δ точка М графика ф-ции f(x) лежит в полосе шириной 2e ограниченной двумя горизонтальными прямыми. Опр:если ф-ция yŠb₁ при xŠa, x<a,то limf(x)=b₁ при хŠа-0. В этом случае число b₁ назыв.пределом ф-ции f(x) в точке х=а слева. Если х>0, то lim_{xŠa+0 f}(x)= b₂, а число b₂ назыв.пределом ф-ции f(x) x=a справа. Пределы слева и справа назыв.односторонними пределами. Можно доказать, что для того чтобы предел ф-ции f(x) при хŠа был=b необходимо и достаточно, чтобы сущ.предел f(x). lim_xŠa f(x)= bÛсущ. lim_{xŠa-0 f}(x)= b и lim_{xŠa+0 f}(x)= b. При определении предела ф-ции в точке не требуется, чтобы ф-ции y=f(x) была определена в точке х=а. При нахождении предела ф-ции рассмотр.знач.ф-ции в окрестности точки а. Число b назыв.lim ф-ции f(x)при xŠ∞ если для любого сколь угодно малого “+”числа e сущ.число N=0,такое что для всех |х|>N выполняется нер-во f(x)-b<e.

№46. Первый замечательный предел

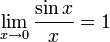
Доказательство

Рассмотрим односторонние пределы 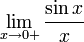и 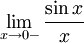и докажем, что они равны 1.

Пусть 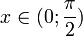. Отложим этот угол на единичной окружности (R = 1).

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.

Очевидно, что:

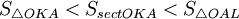(1)

(где S_sectOKA — площадь сектора OKA)

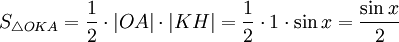
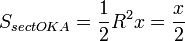
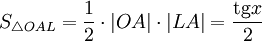
(из 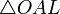: | LA | = tgx)

Подставляя в (1), получим:

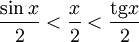
Так как при :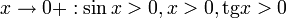

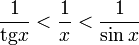
Умножаем на sinx:

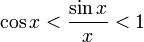
Перейдём к пределу:

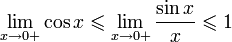
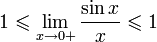
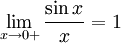
Варианты первого замечательного предела

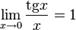
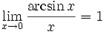
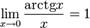
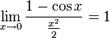
№47. Второй замечательный предел.

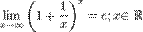
Пусть 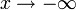. Сделаем подстановку − x = t, тогда

.

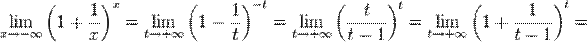
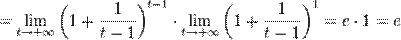Из двух этих случаев вытекает, что 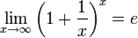для вещественного x.

Варианты второго замечательного.

1. 
2. 
3. 
4. 
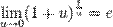
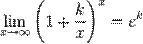
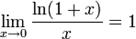
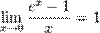
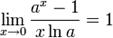5. для ,
6. 

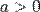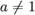
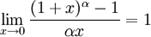
№48. Сравнение бесконечно малых.

Пусть lim_xŠaα(x)=0, lim_xŠaβ(x)=0. Найдём lim_xŠa^α(x)/_β(x)=[⁰/₀].

1)опр.1.если предел отношения ^α(x)/_β(x) при xŠa равен С, где С=const отличное от нуля то α(x) и β(x) называются бесконечно малыми одного и того же порядка, т.е. lim_xŠa^α(x)/_β(x)=С, С=сonst, С=0;

2)опр.2. Если предел α(х), β(x) при xŠa=0, то α(х) называется бесконечно малой величиной более высокого порядка или β(x), т.е. lim_xŠa^α(x)/_β(x)=0; α(х)=0 (β(х)). α(х)–есть 0-мало от β(x).

3)опр.3. Если lim_xŠa^α(x)/_β(x)=1=>назыв. эквивалентными бесконечно малыми.=> α(х)~β(x). 4)опр.4. Если lim_xŠa^α(x)/[β(x)]^k=const, где С≠0, то α(х) называется бесконечно малой величиной порядка k относительно β(x).

5)Опр.5. Если lim_xŠa^α(x)/_β(x)-не сущ., то α(х) и β(x) называются несравнимыми б.м.в. Теорема 1: Если α(х) и β(x) –эквивалентные б.м.в. при xŠa, то α–β – есть б.м.в. более высокого порядка чем α или β. lim_xŠa^α-β/_α=0; lim_xŠa^α-β/_β=0. Док-во: пусть α(х) эквивалентно β(x) при xŠa=> lim_xŠa^α(x)/_β(x)=1= ^β(x)/_α(x)=1. Рассм. lim_xŠa^α-β/_α= lim_xŠa(1-^β/_α)=1-lim_xŠa ^β/_α=1-1=0=> α–β=0(α). lim_xŠa ^α-β/_β= lim_xŠa(^α/_β-1)= lim_xŠa^α/_β -1=1-1=0=> α–β=0(β).

Теорема 2,обратной 1. Если разность 2-х б.м.в. α(х)-β(x) при xŠa есть б.м.в. и относит. α(х) и β(x), то α и β – есть эквивалентные б.м.в.,т.е. α(х)-β(x)=0 (α(х))=>α(х)~β(x) и α(х)-β(x)=0 (β(х))=>α(х)~β(x). Док-во: т.к. α(х)-β(x)=0(α(х))=> lim_xŠa(^{α(х)-β(х)}/_α(х))=0=> lim_xŠa(1-^β/_α)=0=> lim_xŠa 1- lim_xŠa^β/_α=0 или lim_xŠa^β/_α=1=>α(х)~β(x). α(х)-β(x)=0 (β(х))= lim_xŠa ^α-β/_β=0=> lim_xŠa (^α/_β-1)=0=> lim_xŠa ^α/_β=1=> α(х)~β(x).

№57. Односторонние пределы

Если у любой сходящейся к точке x₀ последовательности {x_n} все ее элементы меньше x₀, а соответствующая последовательность 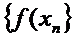сходится к A₁, то число A₁ называется левым пределом функции f(x).

Обозначение: .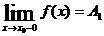

Если у любой сходящейся к 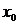последовательности 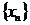все ее элементы больше 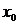, а соответствующая последовательность 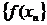сходится к 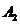, то число 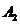называется правым пределом функции f(x):

Обозначение: .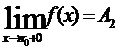

№58. Три определения непрерывности ф-ции в точке. Классификация точек разрыва.

Ф-ция у=f(х) назыв.непрерывной на интервале (а;b) если она непрерывна в каждой точке этого интервала. Опр. lim_xŠa+0f(x)=f(a), то ф-ция f(х) называется непрерывной в точке а справа. lim_xŠb-0f(x)=f(b), то ф-ция f(х) называется непрерывной в точке b слева. Опр: ф-ция у=f(х) назыв. непр.на отрезке [a;b] если она непрерывна в каждой точке интервала (а;b), непрерывна справа в точке а и непрерывна слева в точке b. Если в какой-то точке х_о для ф-ции у=f(х) не выполняется хотя бы одно условие непрерывности, то ф-ция у=f(х) разрывна в точке х_о. В этом случае точка х_о называется точкой разрыва для ф-ции у=f(х). Существуют три вида точек разрыва.

1)если существует предел lim_xŠхоf(x)=a, но он не равен значению ф-ции в точке х_о, тогда точка х_о – точка устранимого разрыва.

2)если существует предел ф-ции f(x) при х стремящемся от х_о справа,т.е. lim_xŠхо+0f(x)=f(x_o+0). Существует предел ф-ции f(x) при хŠх_о слева, т.е. lim_xŠхо-0f(x)=f(x_o-0), но они не равны между собой f(x_o+0)≠f(x_o-0), то х_о-точка разрыва 1-го рода (точка скачка). Разность f(x_o+0)-f(x_o-0)-величина скачка в точке х_о, т.е. всегда от правостороннего отнимается левосторонний.

3)если хотя бы один из односторонних пределов в точке х_о не сущ. или равен ∞, то точка х_о называется точкой разрыва второго рода. $ lim_xŠхо-0f(x)=a; lim_xŠхо+0f(x)=+∞. Примеры 3)-_{(продолжение)} у=^х/_|х|, х≠0 lim_хŠ0+ ^х/_|х|= lim_хŠ0 ^х/_х=1 и lim_хŠ0- ^х/_|х|= lim_хŠ0 ^х/_-х=-1 => по определению, что точка х=0 – точка разрыва 1-го рода.

№59. Непрерывность суммы, произведения и частного непрерывных ф-ций. Непрерывность сложной ф-ции.

Пусть ф-ция у=f(x) задана в некоторой точке хо и некоторой окрестности с центром в точке хо. (см.рис.1.). Придадим аргументу хо некоторое приращение ∆х, т.е. хо+∆х=х, тогда значение ф-ции также изменится. Пусть f(хо)=у. Положим f(хо+∆х)=уо+∆у, тогда ∆у=f(хо+∆х)- f(хо)-приращение ф-ции в точке хо. Опр.:ф-ция у=f(x) называется непрерывной в точке хо, если бесконечно малому приращению аргумента точке хо соответствует бесконечно малое приращение ф-ции в этой точки,т.е. lim∆х0∆у=0 или lim∆х0(f(хо+∆х)- f(хо))=0 или lim∆х0 f(хо+∆х)= f(хо) или limххо f(x)=f(хо) (*),где limххо x=хо. из (*)=>limххо f(x)=f(limххох), т.е. для того чтобы найти предел непрерывной ф-ции в точке хо достаточно подставить в выражение ф-ции вместо аргумента х его значение хо. Пример: докажем: ф-ция у=х2 – непрерывна для любого хо. 1)Возьмём хо. хо=хо+∆х, тогда ф-ция получит приращение ∆у=у(хо+∆х)- у(хо)=(хо+∆х)2-хо2= хо2+2хо*∆х+(∆х)2-хо2=2хо*∆х+(∆х)2. lim∆х0 ∆у= lim∆х0(2хо*∆х+(∆х)2)=0, а это по опр.и означает, что ф-ция y=х2 –непрерывна в любой точке хо.

2)у=sinx, хоR. ∆у=sin(хо+∆х)-sinхо=2sin∆х/2*cos(хо+∆х/2); lim∆х0∆у= lim∆х02sin∆х/2*cos(хо+∆х/2)=0. Аналогично рассматривая каждую осн.элементарную ф-цию можно доказать, что каждая осн.элемент.ф-ция непрерывна в каждой точке, в которой она определена.

Теорема1. f1(x) и f2(x) непрерывна в х=хо. α(х)=f1(x)+f2(x) непрерывна в ххо. Док-во: f1(x) непр.в хо=> limххоf1(x)=f1(xо); f2(x) непр.в хо=> limххоf2(x)=f2(xо); limххоα(х)= limххо(f1(x)+f2(x))= limххоf1(x)+limххоf2(x)= f1(xо)+f2(xо)=α(хо)=>α(х)-непрерывна. Аналогично можно доказать:

1)произведение 2-х непрерывных ф-ций – есть ф-ция непрерывна.

2)частное 2-х непрерывных ф-ций есть ф-ция непрерывная, если знаменатель в рассмотренной точке не равен 0.

3)если ф-ция U=α(x) непрерывна в точке х=хо, а ф-ция f(U) непрерывна в точке U=Uo=α(xo),то сложная ф-ция f[α(x)] будет непрерывна в точке хо. Используя эти теоремы можно доказать теорему2. Можно доказать, что всякая элементарная ф-ция непрерывна в каждой точке, в которой она определена.

№60. Третий и четвертый замечательные пределы. НЕТУ

№61. Непрерывность основных элементарных функций.

Пусть ф-ция у=f(x) задана в некоторой точке х_о и некоторой окрестности с центром в точке х_о. (см.рис.1.). Придадим аргументу х_о некоторое приращение ∆х, т.е. х_о+∆х=х, тогда значение ф-ции также изменится. Пусть f(х_о)=у. Предположим f(х_о+∆х)=у_о+∆у, тогда ∆у=f(х_о+∆х)- f(х_о)-приращение ф-ции в точке х_о. Опр.:ф-ция у=f(x) называется непрерывной в точке х_о, если бесконечно малому приращению аргумента точке х_о соответствует бесконечно малое приращение ф-ции в этой точки,т.е. lim_∆хŠ0∆у=0 или lim_∆хŠ0(f(х_о+∆х)- f(х_о))=0 или lim_∆хŠ0 f(х_о+∆х)= f(х_о) или lim_хŠхо f(x)=f(х_о) (*),где lim_хŠхо x=х_о. из (*)=>lim_хŠхо f(x)=f(lim_хŠхох), т.е. для того чтобы найти предел непрерывной ф-ции в точке х_о достаточно подставить в выражение ф-ции вместо аргумента х его значение х_о. Пример: докажем: ф-ция у=х² – непрерывна для любого х_о. 1)Возьмём -х_о. х_о=х_о+∆х, тогда ф-ция получит приращение ∆у=у(х_о+∆х)- у(х_о)=(х_о+∆х)²-х_о²= х_о²+2х_о*∆х+(∆х)²-х_о²=2х_о*∆х+(∆х)². lim_∆хŠ0 ∆у= lim_∆хŠ0(2х_о*∆х+(∆х)²)=0, а это по опр.и означает, что ф-ция y=х² –непрерывна в любой точке х_о. 2)у=sinx, -х_оÎR. ∆у=sin(х_о+∆х)-sinх_о=2sin^∆х/₂*cos(х_о+^∆х/₂); lim_∆хŠ0∆у= lim_∆хŠ02sin^∆х/₂*cos(х_о+^∆х/₂)=0. Аналогично рассматривая каждую осн.элементарную ф-цию можно доказать, что каждая осн.элемент.ф-ция непрерывна в каждой точке, в которой она определена.

Теорема1. f₁(x) и f₂(x) непрерывна в х=х_о. α(х)=f₁(x)+f₂(x) непрерывна в хÎх_о. Док-во: f₁(x) непр.в х_о=> lim_хŠхоf₁(x)=f₁(x_о); f₂(x) непр.в х_о=> lim_хŠхоf₂(x)=f₂(x_о); lim_хŠхоα(х)= lim_хŠхо(f₁(x)+f₂(x))= lim_хŠхоf₁(x)+lim_хŠхоf₂(x)= f₁(x_о)+f₂(x_о)=α(х_о)=>α(х)-непрерывна. Аналогично можно жоказать: 1)произведение 2-х непрерывных ф-ций – есть ф-ция непрерывна. 2)частное 2-х непрерывных ф-ций есть ф-ция непрерывная, если знаменатель в рассмотренной точке не равен 0. 3)если ф-ция U=α(x) непрерывна в точке х=х_о, а ф-ция f(U) непрерывна в точке U=U_o=α(x_o),то сложная ф-ция f[α(x)] будет непрерывна в точке х_о. Используя эти теоремы можно доказать теорему2. Можно доказать, что всякая элементарная ф-ция непрерывна в каждой точке, в которой она определена

№62. Разрывы функций.

Точка 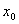называется точкой разрыва функции y = f(x), если она принадлежит области определения функции или её границе и не является точкой непрерывности.

В этом случае говорят, что при x= x₀ функция разрывна. Это может произойти, если в точке x₀ функция не определена или не существует предел 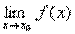, или если предел существует, но .

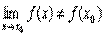Функция не определена в точке x = 0. Эта точка является точкой разрыва 1-го рода, т.к. в ней существуют пределы справа и слева.

Функция 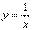разрывна при x = 0. Действительно, при x = 0 функция не определена: .

№63. Асимптоты графика функций. НЕТУ

№64. Производная. Ее механический и геометрический смысл. Уравнение касательной и нормали к графику функции.

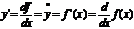Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует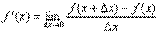

Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.Соответственно, вторая производная функции- скорость изменения скорости, т.е. ускорение

Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Уравнение касательной: y=f(x₀)+f ’(x₀) * (x – x₀)

Составьте уравнение касательной к графику функции в точке M(3; – 2).

Решение. Точка M(3; – 2) является точкой касания, так как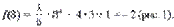

1. a = 3 – абсцисса точки касания.
2. f(3) = – 2.
3. f '(x) = x2 – 4, f '(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – уравнение касательной.

№65. Теорема о непрерывности дифференцируемой ф-ции. Пример непрерывной, но недифференцируемой ф-ции.

Если ф-ция у=f(х) имеет производную в точке х= x_o, т.е. если сущ. предел отношения lim_∆хŠ0^∆у/_∆х= lim_∆хŠ0^{f(x+∆x)-f(x)}/_∆х, то ф-ция у=f(х) называется дифференцируемой в точке х_о. Теорема: если ф-ция у=f(х) дифференцируема в точке х= x_o,то она непрерывна в точке х_о. Док-во: по усл.$ lim_∆хŠ0^∆у/_∆х=f'(x_о)=> ^∆у/_∆х=f'(x_о)+α(∆х), где f'(x_о)Š0 при ∆хŠ0=>∆у=f'(x_о)*∆х+α(∆х)*∆х=>,что если ∆хŠ0, то ∆уŠ0. А это по опр.означает, что ф-ция у=f(x) непрерывна в точке х_о. Обратное утверждение не верно, т.е. если ф-ция непрерывна в точке х_о, то отсюда не следует, что она дифференцируема в этой точке. Пусть f(x)={x,0≤x≤1; 2x-1, 1≤x≤2. Эта ф-ция при х=1 не имеет производной, хотя и непрерывна в этой точке. Пусть ∆х>0. lim_∆хŠ0^∆у/_∆х=lim_∆хŠ0^{f(1+∆x)-f(1)}/_∆х= lim_∆хŠ0^{2(1+∆x)-1-1)}/_∆х= lim_∆хŠ0^2∆x/_∆х=2.Пусть ∆х<0. lim_∆хŠ0^∆у/_∆х=lim_∆хŠ0^{f(1+∆x)-f(1)}/_∆х= lim_∆хŠ0^1+∆x-1)/_∆х= lim_∆хŠ0^∆x/_∆х=1, т.е. рассматриваемый предел зависит от того каков знак ∆х. А это означает, что в точке х=1 ф-ция f(x) производной не имеет. С другой стороны эта ф-ция непрерывна в точке х=1. Если ∆х>0,то ∆у=2∆х, а если ∆х<0,то ∆у=∆х=>при ∆хŠ0, ∆уŠ0, т.е. у=f(x) непрерывна в х=1. из теоремы следует, что в точках разрыва ф-ция не может иметь производной.

Примеры вычисления производной.: 1)степенная ф-ция у=х^α,αÎR,x>0. Дадим аргументу х приращение ∆х и получим х+∆х. ∆у=у(х+∆х)-у(х)=(х+∆х)^α-х^α=х^α(1+^∆х/_х)^α-х^α= х^α((1+^∆х/_х)^α-1). у'=lim_∆хŠ0^∆у/_∆х=lim_∆хŠ0(х^α(1+^∆х/_х)^α-1)/_∆х= х^αlim_∆хŠ0^α*∆х/х/_∆х= х^αlim_∆хŠ0^α/_х=α*х^α-1. (х^α)'=α*х^α-1.-эта формула верна для любого х из области опр.ф-ции. (х)'=1(α=1); (¹/_х)'=-¹/х²(α=-1); (√х)'=¹/_2√х(α=½)

№66. производная постоянной суммы разности произведения и частного. НЕТУ

№67. Производная сложной функции и обратной.

Производная сложной функции равна произведению производной внешней функции на производную от внутренней функции.

1)Рассмотрим ф-цию y=arcsinx;-1≤x≤1.Обратной этой ф-ции явл. x=siny (-π/2≤y≤π/2) Причём производная обратной ф-ции сущ. x’(y)=cosy;≠0;для любого у из(-π/2;π/2) =>по теореме о дифф. Обратной ф-ции имеем y’(x)=1/x’(y)=1/cosy=1/cos(arcsinx)=1/√(1-sin²(arcsinx))=1/√(1-x²) (arcsinx)’=1/√(1-x²) Аналогично (arccosx)’= -1/√(1-x²) xε(-1;1) 2)y=arctgx x xε(-∞;∞)Обратная x=tgy -π/2≤y≤π/2 Производная обратной ф-ции сущ. x’(y)=1/cos²y≠0 для любого у ε(-π/2;π/2) ) =>по теореме о дифф. Обратной ф-ции имеем y’(x)=1/x’(y)=cos²y=cos²(arctgx)=1/1+tg²(arctgx)=1/1+x² (arctgx)’=1/1+x² xε(-∞;∞) Аналогично (arсctgx)’= -1/1+x²) (с графиками).

№68. Производная показательно-степенной функции. Производные тригонометрических функций.

А)Функция называется показательной, если независимая переменная входит в показатель степени, и степенной, если переменная является основанием. Если же и основание и показатель степени зависят от переменной, то такая функция будет показательно – степенной.

Пусть u = f(x) и v = g(x) – функции, имеющие производные в точке х, f(x)>0.

Найдем производную функции y = u^v. Логарифмируя, получим:

lny = vlnu

Б) Производная от y=sinx, это y’=cosx. Дадим аргументу x приращение ∆x; тогда 1) y+∆y=sin(x+∆x); 2) ∆y=sin(x+∆x)-sinx=2sin ;

3) ; 4) 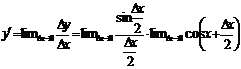, но так как 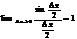, то 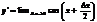=cosx. Последнее равенство получается на том основании, что cosx есть непрерывная функция. Так же y=cosx y’=-sinx. Производная от y=tgx, равна . По правилу дифференцирования дроби получаем: . Так же y=ctgx, равен .

№69. Производная логарифмической функции. Производная степенной и показательной функций.

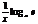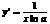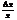А)Производная от log_ax, равна или . Если ∆y есть приращение функции y=log_ax, соответствующее приращению ∆x аргумента x, то y+∆y=log_a(x+∆x); ∆y=log_a(x+∆x)-log_ax= . Помножим и разделим на x выражение, состоящее в правой части последнего равенства . Обозначим величину через α. Очевидно, при 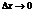и данном x. Следовательно, 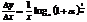, но как известно . Если же выражение, стоящее под знаком логарифма, стремится к числе e, то логарифм этого выражения стремится к log_ae (в силу непрерывности логарифмической функции). Поэтому окончательно получаем: 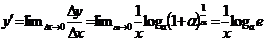. Заметив, что , полученную формулу можно переписать так:.

Б) Производная от (показательная функция) функции a^x, где а > 0, равна a^xlna, т.е. y=a^x, равна y’=a^xlna. Логарифмируя равенство y=a^x, получим: lny=xlna или y’=a^xlna. Если оснавание а=е, то lne=1 и мы получим y=e^x, y’=e^x.

№70. Производные обратных тригонометрических функций.

1)Рассмотрим ф-цию y=arcsinx;-1≤x≤1.Обратной этой ф-ции явл. x=siny (-π/2≤y≤π/2) Причём производная обратной ф-ции сущ. x’(y)=cosy;≠0;для любого у из(-π/2;π/2) =>по теореме о дифф. Обратной ф-ции имеем y’(x)=1/x’(y)=1/cosy=1/cos(arcsinx)=1/√(1-sin²(arcsinx))=1/√(1-x²) (arcsinx)’=1/√(1-x²) Аналогично (arccosx)’= -1/√(1-x²) xε(-1;1) 2)y=arctgx x xε(-∞;∞)Обратная x=tgy -π/2≤y≤π/2 Производная обратной ф-ции сущ. x’(y)=1/cos²y≠0 для любого у ε(-π/2;π/2) ) =>по теореме о дифф. Обратной ф-ции имеем y’(x)=1/x’(y)=cos²y=cos²(arctgx)=1/1+tg²(arctgx)=1/1+x² (arctgx)’=1/1+x² xε(-∞;∞) Аналогично (arсctgx)’= -1/1+x²) (с графиками).

№71. Гиперболические ф-ции и их производные.

Ф-ция y=e^x-не явл. ни чётной,ни нечётной,но её можно представить в виде суммы двух слагаемых из которых одно:чётная ,второе-нечётная ф-ция e^x=(e^x+e^-x)/2+(e^x-e^-x)/2

(e^x+e^-x)/2=chx-гиперболический cos (чётная)

(e^x-e^-x)/2=shx-гиперболический sin(нечётная)shx/chx=thx

chx/shx=cthx

Св-ва гиперболических ф-ций напоминают св-ва тритгонометрпических ф-ций

ch²x-sh²x=1; ch²x+sh²x=ch2x; 2shx *chx=sh2x

Найдём произв.от тригонометрич.ф-ций: (shx)’=chx; (chx)’=shx ;thx=1/ch²x;

(cthx)’= -1/sh²x

№72. Логарифмическое дифференцирование, производная степенно-показательной функции.

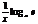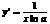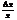Производная от log_ax, равна или . Если ∆y есть приращение функции y=log_ax, соответствующее приращению ∆x аргумента x, то y+∆y=log_a(x+∆x); ∆y=log_a(x+∆x)-log_ax= . Помножим и разделим на x выражение, состоящее в правой части последнего равенства . Обозначим величину через α. Очевидно, при 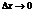и данном x. Следовательно, 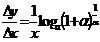, но как известно . Если же выражение, стоящее под знаком логарифма, стремится к числе e, то логарифм этого выражения стремится к log_ae (в силу непрерывности логарифмической функции). Поэтому окончательно получаем: 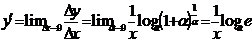. Заметив, что , полученную формулу можно переписать так: .

№73. Производные высших порядков.

Пусть ф-ия y=f(x), xÎ[a;b] дифференцируема на [a;b], производная в общем случае сама зависит от х, поэтому можно говорить о производной полученной ф-ии. Производная от производной первого порядка наз. производной второго порядка и обозначается y’’ или y’’(x), таким образом y’’=[y’(x)]. Производная от производной второго порядка наз. производной третьего порядка. Вообще производной n-ого порядка наз. производная от производной n–1-ого порядка, y⁽ⁿ⁾=[y^(n-1)(x)]’. Производные четвёртого, пятого и т.д. порядков обозначаются римскими цифрами. (U±V)⁽ⁿ⁾=U⁽ⁿ⁾±V⁽ⁿ⁾; (UV)⁽ⁿ⁾=U⁽ⁿ⁾V+nU^(n-1)V’+((n(n-1))/1×2)U^(n-2)V’’+…+UV⁽ⁿ⁾ - Формула Лейбница.

№74. Производные неявных и параметрических ф-ций.

Неявн.Пусть знач.x и y связаны некоторым ур-ем F(x;y)=0(1)Если ф-ция y=f(x)определена на интервале(ab),такова что ур-е(1)при подстановке в него вместо y выраж.f(x)обращается в ождество относительно x,то ф-ция y=f(x)есть неявная ф-ция,определёная ур-ем(1) Но не всякую неявно заданную ф-цию можно представить явно.Например y-x-siny=0

не всякую явно заданную ф-цию можно представить неявно При вычисл.знач. произв.неявной ф-ции при данном знач.ар-та,нужно знать ещё и знач.ф-ции y,при данном знач.аргумента Парам. {x=α(t); y=λ(t)(1)T1≤t≤T2 Каждому значению t соответствуют значения x и y.Если рассматривать x и y как координаты точки на плоскости XOY,то каждому значению t будет соответствовать определённая точка на плоскости.Когда t изменяется от T1 до Т2,то эта точка на пл-ти описывает некоторую кривую.Ур-я(1)называются параметр.ур-ями этой кривой,t параметром.А способ задания кривой ур-ями(1)называется параметрическим. Пусть ф-ция x=α(t)имеет обратную t=Ф(x),тогда y явл.сложной ф-цией от x.y=α[Ф(х)]Таким образом ур-я (1)определяют у как ф-цию от х , и говорят что эта ф-ция у(х)задана параметр. Найдём произв.ф-ции заданой ур-ями (1).Предположим ,что α(t),λ(t)имеют произв.,кроме того ф-ция х=λ(t),имеет обратную t=Ф(х),которая также имеет производную,тогда ф-цию у=f(x)можно рассматр. Как сложную ф-цию у=λ[Ф(х)] ,t=Ф(х)-промежуточный аргумент y'(x)=y’(t) *t’(x)по правилу дифф. Обратной ф-ции.y’(x)=y’(t)/x’(t) или y’(x)=λ’(t)/α’(t).

№75. Дифференциал ф-ции, его геометрический смысл.

Пусть ф-ция y=f(x)дифф.на отр.ab,существует f’(x)=lim(∆xà0)∆y/∆x => ∆y/∆x=f’(x)+α,где αà0. ∆y=f’(x)∆x+α∆x (1)Т.к. в общем случае f’(x)≠0,то при постоянном х и переменном ∆х→0,первое слагаемое в рав-ве(1)есть б.м.в.,того же порядка что ∆х.Авторое слагаемое-б.м.в. более высокого порядка чем ∆х lim(∆x→0)α∆x/∆x=0. Таким образом приращение ф-ции ∆у состоит из двух слагаемых из которых 1-ое –главная часть приращения относительно ∆х f’(x)∆x-называют дифференциалом ф-ции и обозначают dy или df(x) dy= f’(x)∆x По опр. Полагают,что дифф. Переменного dx=∆x Это опр. Оправдано,т.к.если y=х,то dy=dx=∆x dx=∆x dy=f’(x)dx,отсюда f’(x)=dy/dx.Т.е. произв. можно представить как отношение дифференциала ф-ции к дифф. арг-та Из (1)=> ∆y=dy+α∆x Т.е. приращение ф-ции отлич.от диф. На б.м.в.более высокого порядка чем ∆х α∆х-б.м.в.более высокого порядка,чем dy.Поэтомув приближённых вычислениях пользуются равенством ∆y≈dy f(x+∆x)≈f(x)+f’(x)∆x-формула для приближ.вычислений.Правила относящиеся к производным сохр. и для дифференциаловПример y=tg²xdy=2tgx*1/cos²x*dx

Геометр.смысл.дифференциала Рассмотрим y=f(x)и соотв. ей кривую(рисунок) NT=MNtgα=∆xf’(x)=dy таким образом, дифф.ф-ции y=f(x) соответств.данным значениям х и ∆х равен приращению ординаты касательной к гр-ку ф-ции f(x) в точке х.

№76. Теорема Ролля.

Если функция непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.

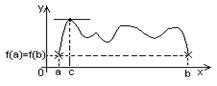
№77. Теорема Лагранжа.

Формула конечных приращений

F ‘(c) = Δf/Δx (приращение функции/ приращение аргумента)

или теорема о среднем значении утверждает, что если функция f непрерывна на отрезке [a;b] и дифференцируема в интервале (a;b), то найдётся такая точка 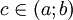, что .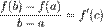

Геометрически: на отрезке [a;b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.

Физически: Пусть f(t) — расстояние точки в момент t от начального положения. Тогда f(b) − f(a) есть путь, пройденный с момента t = a до момента t = b, отношение — средняя скорость за этот промежуток.

Vср=S(t2)-S(t1) / t2 – t1

№78. Теорема Коши.

Пусть даны две функци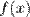и и 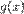такие, что:

1. и 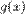определены и непрерывны на отрезке ;
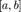2. производные 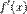и конечны на интервале ;
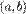3. производные 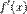и 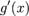не обращаются в ноль одновременно на интервале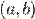
4. ;

тогда

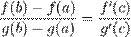, где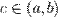

Доказательство

Для доказательства введём функцию

Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны f(a). Воспользовавшись упомянутой теоремой, получим, что существует точка c, в которой производная функции F равна нулю, а равна как раз необходимому числу.

№79. . Правило Лопиталя.

Метод нахождения пределов функций, раскрывающий неопределённости вида 0 / 0 и .

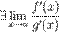=> . н/р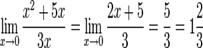

№80. Многочлен Тейлора.

Опр. Пусть ф-ция f(x) имеет в т-ке а и некоторой ее окрестности пр-ные порядка n+1. Пусть х - любое значение аргумента из указанной окрестности, х¹а. Тогда между т-ми а и х надутся т-ка e такая, что справедлива ф-ла Тейлора. f(x)=f(a)+f‘(a)/1!(x+a)+f‘‘(a)/2!(x+a)^2+f^(n)(а)/n!+f^(n+1)(e)/ (n+1)!(x-a)^(n+1).Док-во. Сводится к Роллю путем введения вспом. переменной g(x). g(x)=f(x)-f(a)-f‘(x)(x-a)-…-1/n!*f^n(x)(x-a)^n-1/(n+1)!(x-a)^n+1*l. По т-ме Роляя $ т-ка с из (a,b), такая что g(c)=0 l=f^(n+1)(c).

№81. Необходимые и достаточные условия возрастания и убывания ф-ции.

1)Пусть ф-ция f(x)на отр.[ab] имеет произв. f’(x),x э .[ab] и возр.на этом отр.,тогда f’(x)>0 для люб. x э .[ab] 2)Если ф-ция y=f(x) непрер.на отр. .[ab],дифференц. в(ab),причём f’(x)>0 для люб. x э .[ab] =>f(x) строго возр.на.[ab]

Док-во 1)Дадим аргументу x приращение ∆х f(x+∆x)-f(x)/∆x Т.к. y=f(x) возр.,то f(x+∆x)-f(x)/∆x>0,при ∆x>0; f(x+∆x)-f(x)/∆x<0,при ∆x<0 Перейдём к lim при ∆x®0 lim(∆x®0) f(x+∆x)-f(x)/∆x=f’(x)≥0 2)Пусть f’(x)>0 для люб. x э .[ab] ,т.к.ф-ция непрерывна на отр. .[ab],то к ней можно применить теорему Лагранжа о конечных приращениях .Возьмём любые 2 точки х1,х2,х1<x2; f(x2)-f(x1)=f’(c)(x2-x1) => f(x2)-f(x1)>0 =>f(x2)> f(x1) =>ф-ция возр. Аналогичная теорема имеет место и для убыв.ф-ции Замечания 1)Если ф-ция возр.,то касательная к граф.ф-ции в любой точке отр.[ab] образует острый угол с осью Ох,или горизонтальна tgα=f’(x) ≥0 2)Если убыв. То тупой угол.

№82. Максимум и минимум ф-ции. Необходимый признак существования экстремума ф-ции, его недостаточность.

Опр.