Замкнутые классы булевых функций

Полное описание всех замкнутых классов было дано американским математиком Э. Постом:

Класс функций сохраняющих ноль .

Определение:

Говорят, что функция сохраняет ноль, если .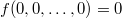

Класс функций сохраняющих единицу .

Определение:

Говорят, что функция сохраняет один, если .

Класс самодвойственных функций .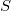

Определение:

Говорят, что функция самодвойственна, если 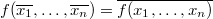. Иными словами, функция называется самодвойственной, если на противоположных наборах она принимает противоположные значения.

Класс монотонных функций .

Определение:

Говорят, что функция монотонна, если .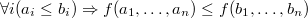

Класс линейных функций .

Определение:

Говорят, что функция линейна, если существуют такие , где , что для любых 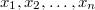имеет место равенство: .

6) полные классы. Теорема Поста.

Множество булевых функций называется полной системой, если замыкание этого множества совпадает с множеством всех функций.

Американский математик Эмиль Пост сформулировал необходимое и достаточное условие полноты системы булевых функций. Для этого он ввел в рассмотрение следующие замкнутые классы булевых функций:

§ Функции, сохраняющие константу и ;

§ Самодвойственные функции ;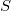

§ Монотонные функции ;

§ Линейные функции .

7) Графы, простые графы, матрица инценднтности и смежности.

Граф - пара G=(V,E), где V - множество объектов произвольной природы, называемых вершинами а E - семейство пар e_i=(v_i1, v_i2), v_ijÎV, называемых ребрами .В общем случае множество V и/или семейство E могут содержать бесконечное число элементов, но мы будем рассматривать только конечные графы, т.е. графы, у которых как V, так и E конечны.

Две вершины называются смежными, если они соединены ребром (дугой). Смежные вершины называются граничными вершинами соответствующего ребра (дуги), а это ребро (дуга) - инцидентным соответствующим вершинам.

Граф называется полным, если каждые две вершины его соединены одним и только одним ребром.

Деревом называется произвольный связный граф без циклов.

Степень вершины называется число рёбер графа, которым принадлежит эта вершина.

Маршрутом в графе называется чередующаяся последовательность вершин и рёбер, в которой любые два соседних элемента инцидентны

Путём называется последовательность дуг (в ориентированном графе), такая, что конец одной дуги является началом другой дуги.

Простой путь – путь, в котором ни одна дуга не встречается дважды.

Цепью называется множество рёбер (в неориентированном графе), которые можно расположить так, что конец (в этом расположении) одного ребра является началом другого. Другое определение: цепь – последовательность смежных вершин. Замкнутая цепь называется циклом.

Петлёй называется ребро, у которого начальная и конечная вершины совпадают.

Графы G₁=(V₁,E₁) и G₂=(V₂,E₂) называются изоморфными (обозначение: G₁~G₂), если между графами существует взаимно-однозначное отображение j: G₁<G₂ (V₁<V₂, E₁<E₂), которое сохраняет соответствие между ребрами (дугами) графов, т.е. для любого ребра (дуги) e=(v,u) верно: e'=j(v,u)=(j(v),j(u)) (eÎE₁, e'ÎE₂). Отображение j называется изоморфным отображением.

Иными словами, изоморфные графы различаются только обозначением вершин.

Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размераn, в которой значение элемента a_ij равно числу рёбер из i-й вершины графа в j-ю вершину.

· Матрица инцидентности — одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина). Столбцы матрицы соответствуют ребрам, строки — вершинам. Ненулевое значение в ячейке матрицы указывает связь между вершиной и ребром (их инцидентность).. Не используется для графов с петлями, так как у петель одна вершина является и началом, и концом.

· В каждом столбце должны стоять две единицы, а все остальные символы - нули.

8) Связные графы, неравенство m>=n-k

Граф связанный,если любые две вершины соеденены маршрутом.

Компонентная связанность графа -непустое подмножество вершин.Каждая точка явл компонентной связанностью. Граф называется вершинно 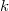- связным, если удаление любых 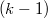вершин оставляет граф связным.

n-кол-во вершин, m-кол-во ребер,k-связанность => n-k<=m

9) леса и деревья (m=n-1, m=n-k)

Лес - граф,в котором нет циклов.

Листок-вершина дерева степени.

Деревом называется произвольный связный граф без циклов(связанный лес).

Мост-ребро,при удалении которого увеличивается кол-во компонентов связанности;не участвовашее ни в одном цикле.

Лес-граф,все ребра которого явл мостами.

Если m- кол-во ребер дерева из n-вершин,то m=n-1

10) плоские графы, Формула Эйлера. Неплонарность K33 и K5

Цикл, проходящий через все рёбра графа, называют эйлеровым,а граф, содержащий эйлеров цикл, — эйлеровым графом.

Формула Эйлера: f=m-n+2 m-колво ребер, n-колво вершин,f-колво граней плоского графа

Планарный граф(плоский) — граф, который может быть изображен на плоскости без пересечения ребер.( никакие два ребра не имеют общих точек, кроме инцидентной им обоим вершины.)