Спектральная плотность стационарных

СЛУЧАЙНЫХ ПРОЦЕССОВ

Если интеграл 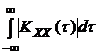сходится, т.е. стационарный процесс обладает свойством эргодичности, то корреляционная функция может быть представлена в виде двойного интеграла Фурье:

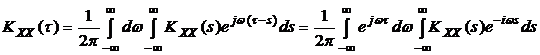. (3.1)

Введем обозначение

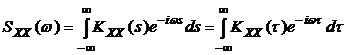. (3.2)

Тогда

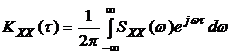. (3.3)

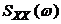называется спектральной плотностью случайного процесса , а прямое (3.2) и обратное (3.3) преобразования Фурье – преобразованиями Хинчина-Винера.

Поясним физический смысл введенного понятия спектральной плотности СП.

Рассмотрим простейший электрический контур, состоящий из источника напряжения и резистора с сопротивлением R=1 Ом (рис.3.1). Предположим, что на вход схемы подается напряжение в виде центрированного случайного процесса ( флуктуация напряжения) -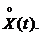

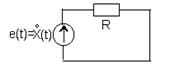Средняя мощность, поглощаемая в сопротивлении за

интервал времени Т, определится как .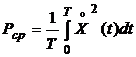

Рис.3.1 Но в случае эргодического процесса его дисперсия будет: 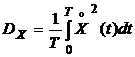. Следовательно 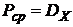. Дисперсия же процесса может быть выражена через его спектральную плотность:

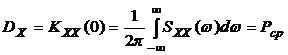. (3.4)

Средняя мощность, выделяемая в сопротивлении в частотном диапазоне 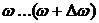, определится как:

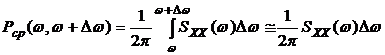. (3.5)

Из (3.5) следует, что

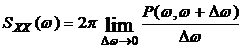. (3.6)

Таким образом, спектральная плотность характеризует распределение мощности флуктуационных потерь по частотам, т.е. может рассматриваться как плотность мощности флуктуационных потерь на различных частотах w, образующих непрерывный спектр.

Получим выражение для спектральной плотности процесса, характеризующегося корреляционной функцией вида 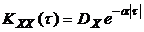. В этом случае

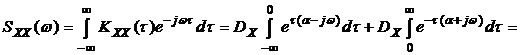
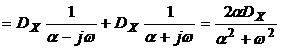. (3.7)

Зависимость спектральной плотности (3.7) от частоты w приведена на рис.3.2.

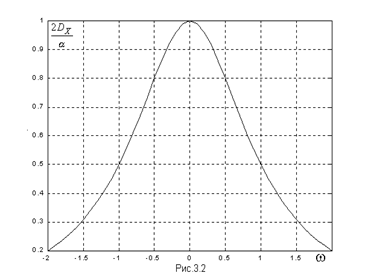
При решении ряда практических задач вместо преобразований Фурье над корреляционной функцией стационарного процесса целесообразно воспользоваться

двухсторонним преобразованием Лапласа. Такое преобразование можно получить на основе (3.2) и (3.3), положив в них :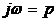

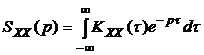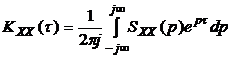, . (3.8)

Необходимость двухстороннего преобразования Лапласа вместо обычно применяемого при исследовании переходных процессов в контурах вызвано тем, что аргумент t меняется в пределах 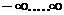, тогда как при одностороннем преобразовании Лапласа аргумент t изменятся от 0 до .

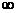Будем далее 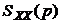называть операторной спектральной плотностью случайногопроцесса X(t). Для практического определения корреляционной функции при известной операторной спектральной плотности целесообразно воспользоваться теорией вычетов в полюсах, лежащих на комплексной плоскости p при t>0 слева от оси ординат (l_k,), а при t< 0 - справа от этой оси (m_k) [1,2]:

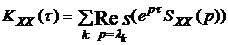при t>0; (3.9)

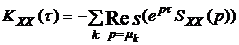при t<0. (3.10)

Аналогично могут быть определены и взаимные корреляционные функции:

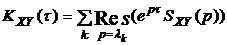при t>0; (3.11)

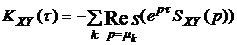при t<0. (3.12)

Операторную спектральную плотность, представляющую собой двухстороннее преобразование Лапласа над корреляционной функцией, можно выразить и через односторонние преобразования Лапласа:

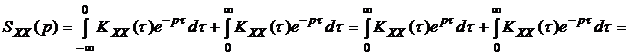
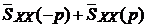= , (3.13)

где 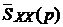- одностороннее преобразование Лапласа,

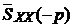- одностороннее преобразование Лапласа при замене p на –p.

Обратные преобразования в этом случае будут:

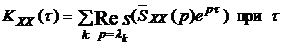>0, (3.14)

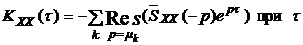<0. (3.15)

Если в выражение для спектральной плотности процесса (3.7) подставить 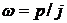, то

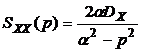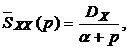
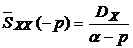, . (3.16)

Беря оригинал от 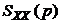при t>0 (полюс 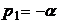), получим

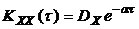(t>0).

При t<0 (полюс 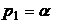), будем иметь

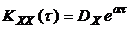(t<0).

Объединение полученных выражений для t>0 и t<0 дает известную аппроксимацию корреляционной функции:

.

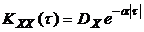ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СТАЦИОНАРНЫХ

СЛУЧАЙНЫХ ПРОЦЕССОВ