Модулированные колебания. Амплитудная модуляция.

Для передачи информации по каналу связи необходимо иметь переносчик в качестве которого может служить любой физический процесс, протекающий во времени и способный распространяться в пространстве. Переносчиками информации могут быть электромагнитные и звуковые волны, свет (тоже эл.м.в.) В электросвязи в качестве носителя информации используется электрический ток, способный легко распространяться по проводам на большие расстояния. Нанесение информации на переносчик называют модуляцией. В самом общем случае сигнал, несущий в себе информацию, можно представить в виде соотношения

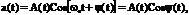
где A - амплитуда, w₀ - частота, j(t) - фаза колебания, y(t) - угол колебания. Различают амплитудную (АМ) и угловую модуляцию (УМ). Сигнал занимает определенный участок электромагнитного спектра Dw. Как правило, выполняется соотношение Dw/w₀ << 1. т.е. любое модулированное колебание есть узкополосный процесс. Спектр речи до 6000 Гц, при несущей 150 кГц Fmax /f₀ = 6 ×10³ /1,5 ×10⁵ = 0,04 << 1, для ТV Fmax = 6 МГц, f₀ ³ 50 МГц, Fmax / f₀ = 0,12 << 1.

Процесс модуляции приводит к сложному преобразованию спектра сигнала. Модуляция приводит к 1) расширению спектра и 2) переносу его в область несущей частоты.

Рисунок

К основным видам аналоговой модуляции относятся: амплитудная (АМ), фазовая (ФМ) и частотная (УМ) модуляция. Разновидностями АМ являются балансная (БМ) и однополосная (ОМ) модуляция. Общее выражение для АМ колебания имеет вид а(t) = А(t) Cos(w₀t + 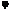₀). Для тональной АМ S(t) = S₀ Cos( 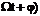и A(t) = A₀ + K _AM × S(t) + A₀ + DAm Cos( 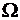t +j), где 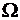- частота модуляции, Кам - коэффициент пропорциональности, DAм = Кам × S₀ - амплитуда изменения огибающей. Отношение М = D A_м/A₀ называется коэффициентом модуляции и характеризует глубину изменения огибающей амплитуд.

Рисунок

Амплитуда колебаний при М £ 1 изменяется от A_min = A₀ (1-M) до А_max = А₀ (1 + М), М = 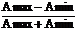. Средняя за период модуляции мощность равна среднему квадрату амплитуды А(t) A²(t) = A²₀(1 + 0,5 M²) = A²₀ 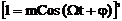пиковая мощность равна 4Р₀, а средняя - 1,5 Р₀. При модуляции одним тоном, когда s(t) = cos Wt

a(t) =A₀(1+M CosWt)Cosw₀t = A₀Cosw₀t + +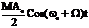

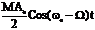+ . Как известно CosL ×Cosb = 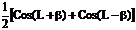. Эта формула определяет спектральный состав одноканального АМ-сигнала, здесь w₀ + W - верхняя боковая частота, w₀ - W - нижняя боковая частота.

Рисунок

Ширина спектра при АМ в два раза шире спектра сообщения F_max; D¦ = 2 F_max.

Возможна балансная АМ с подавлением несущего колебания БМ, а также модуляция с одной боковой полосой частот (ОМ) (ОБП, SSB - Single side bana).Системы БМ и ОМ позволяют сократить бесполезный расход энергии на составляющую несущей частоты, а при ОМ - вдвое сократить ширину спектра передаваемого сигнала.

14, Модулированные колебания. Угловая модуляция. Для передачи информации по каналу связи необходимо иметь переносчик в качестве которого может служить любой физический процесс, протекающий во времени и способный распространяться в пространстве. Переносчиками информации могут быть электромагнитные и звуковые волны, свет (тоже эл.м.в.) В электросвязи в качестве носителя информации используется электрический ток, способный легко распространяться по проводам на большие расстояния. Нанесение информации на переносчик называют модуляцией. В самом общем случае сигнал, несущий в себе информацию, можно представить в виде соотношения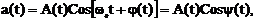

где A - амплитуда, w₀ - частота, j(t) - фаза колебания, y(t) - угол колебания. Различают амплитудную (АМ) и угловую модуляцию (УМ). Сигнал занимает определенный участок электромагнитного спектра Dw. Как правило, выполняется соотношение Dw/w₀ << 1. т.е. любое модулированное колебание есть узкополосный процесс. Спектр речи до 6000 Гц, при несущей 150 кГц Fmax /f₀ = 6 ×10³ /1,5 ×10⁵ = 0,04 << 1, для ТV Fmax = 6 МГц, f₀ ³ 50 МГц, Fmax / f₀ = 0,12 << 1.

Процесс модуляции приводит к сложному преобразованию спектра сигнала. Модуляция приводит к 1) расширению спектра и 2) переносу его в область несущей частоты.

Рисунок

К основным видам аналоговой модуляции относятся: амплитудная (АМ), фазовая (ФМ) и частотная (УМ) модуляция. Разновидностями АМ являются балансная (БМ) и однополосная (ОМ) модуляция.

Угловая модуляция. Сигнал с угловой модуляцией определяется соотношением а(t) = A₀ Cos [w₀t + j(t) ] = A₀ Cos y (t)/ Полная фаза (угол) ВЧ колебания y(t) = w₀t + j(t), а мгновенная частота колебания изменяется по закону производной w (t) = 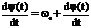. Наоборот, при изменении частоты по закону w(t) , фаза колебания y(t) , будет изменяться по закону интеграла от w(t) y(t) + 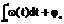. Для фазовой модуляции (ФМ)

y(t) = j₀ + Dj_мS(t) и имеем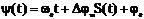

a(t) = A₀Cos[w₀t + Dj_м S(t) +j₀] (ФМ)

При ЧМ по закону передаваемого сообщения изменяется частота несущего колебания 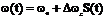, где 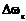- амплитуда частотного отклонения (девиация частоты). Полная фаза колебания при этом будет равна:

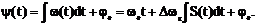
Выражение ЧМ сигнала записывается в виде

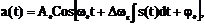(ЧМ)

когда модуляция одним тоном s(t) = CosWt выражения сигнала при ФМ и ЧМ по форме имеют одинаковый вид:

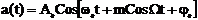ФМ m =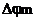

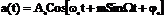индекс угловой модуляции ЧМ m = 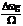Для определения спектра при 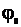= 0 заменим косинус суммы двух углов по известным формулам тригонометрии Cos (L +b) + Cos b CosL- Sinb SinL

a(t) = 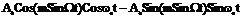. Из теории бесселевых функций известны следующие соотношения

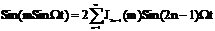
функция Бесселя (порядка) индекса

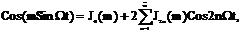
где Jn(m) - бесселева функция первого рода n-го порядка от аргумента m

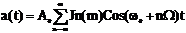более компактный вид. Окончательно получим: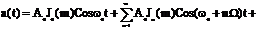

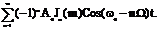+ Даже при синусоидальных ЧМ и ФМ получается теоретически безграничный спектр.

Он состоит из несущей и двух боковых полос ( 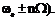Амплитуда несущей А₀ J₀ (m) при ЧМ и ФМ (в отличие от АМ) зависит от модулирующего колебания. При значениях m = 2,3; 5,4 и др. J₀ вообще будет равна нулю. Амплитуда боковых частот равна 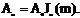Практически же ширина спектров ЧМ и ФМ сигналов ограничена.

Рисунок

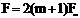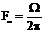Амплитуды боковых частот быстро убывают с увеличением номера гармоники n. При n > m составляющие спектра малы и ими можно пренебречь. Практически ширина спектра при угловой модуляции равны ,где - частота модулирующего колебания. Различие между ЧМ и ФМ проявляется только при изменении частоты модуляции W. При УМ m = ( 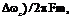поэтому при m >> 1 полоса 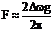практически не зависит от частоты модулирующего колебания F_m.

При ФМ m = 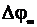и m >> 1 ширина спектра будет равна 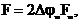т.е. она зависит от модулирующей частоты. В этом и состоит различие в спектрах УМ и ФМ. В ЧМ девиация 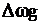пропорциональна амплитуде НЧ сигнала и не зависит от частоты модулирующего колебания Fm. При ФМ ее индекс

m = Dj_m пропорционален амплитуде НЧ сигнала независимо от его частоты, поэтому девиация частоты при ФМ линейно увеличивается с ростом частоты W (Fm).

Рисунок

Кроме структуры колебания УМ и ФМ различаются и способом осуществления. При УМ обычно применяют прямое воздействие на частоту автогенератора. При ФМ генератор имеет стабильную частоту, а фаза колебания моделируется в одном из последующих элементов устройства.

15. Дискретная модуляция часто называется манипуляцией. Устройство осуществляющее дискретную модуляцию называют манипулятором или генератором сигналов. При АМ_Н символу 1 соответствуют передача несущей в течение времени t₀ (посылка, символу 0 - отсутствие колебания (пауза).

Рисунок

При ЧМ_Н несущей с f₁ соответствует символ 1, f₀ - символ "0". При ФМ_Н фаза несущей меняется на 180⁰ при каждом переходе от 1 к 0 и от 0 к 1.

При ОФМ_Н фаза несущей изменяется на 180⁰ при передаче "1" и остается неизменной при передаче "0" (или наоборот). При импульсной модуляции переносчиком информации служит периодическая последовательность импульсов одинаковой формы. При АНМ изменяется амплитуда импульса

A(t) = A₀ + DAs(t). При ШИМ изменяется длительность импульса 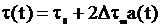где 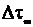- максимальное отклонение импульса в одну сторону. При ЧИМ изменяется частота следования импульсов. При ФИМ - сдвиг импульсов относительно тактовых точек 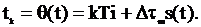Ширина спектра последовательности импульсов практически не зависит от частоты повторения 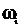и определяется шириной спектра одного импульса. Поэтому рабочая полоса частот, занимаемая импульсными сигналами, практически не зависит от вида модуляции и определяется длительностью и формой импульса. В теории связи вводится понятие базы сигнала 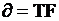- его спектральная полоса для простых сигналов 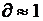, для сложных 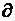>>1. На практике нашли применение шумоподобные сигналы (не являющиеся случайными), сформированные по определенному алгоритму. Эти сигналы относятся к типу широкополосных (ТF >> 1). Относят псевдослучайные м - последовательности Хаффмена, коды Баркера, сигналы Пэли-Плоткина. При НКМ передача отдельных значений сигнала сводится к передаче определенных групп импульсов друг за другом через относительно большие промежутки времени по сравнению с t отдельных импульсов.

16. Помехоустойчивость системы связи. Оптимальный фильтр.

Обычно способ передачи (т.е. способ кодирования и модуляции) задан и нужно определить помехоустойчивость, которую обеспечивают различные способы приема. Возникает вопрос - какой из возможных способов приема является оптимальным? Указанные вопросы являются предметом рассмотрения теории помехоустойчивости, основы которой разработаны акад. В.А. Котельниковым. Помехоустойчивостью системы связи называется способность системы противостоять вредному действию помех и различать (восстанавливать) сигналы с заданной достоверностью. Задача определения помехоустойчивости всей системы в целом весьма сложна. Поэтому часто определяют помехоустойчивость отдельных звеньев системы: 1) приемника при заданном способе передачи, 2) системы модуляции при заданном способе приема и т.д. Предельно достижимая помехоустойчивость называется, по Котельникову, потенциальной помехоустойчивостью. Сравнение потенциальной и реальной помехоустойчивости позволяет дать оценку качества реального устройства и найти еще неиспользованные резервы. Например, зная потенциальную помехоустойчивость приемника, можно судить, насколько близка к ней реальная помехоустойчивость существующих способов приема и насколько целесообразно их дальнейшее усовершенствование при заданном способе передачи. Сведения о потенциальной помехоустойчивости приемника при различных способах передачи позволяют сравнивать эти способы передачи между собой и указать, какие из них являются наиболее совершенными.

Обеспечение высокой помехоустойчивости систем связи осуществляется в принципе двумя путями: а) можно совершенствовать структуру передаваемых сигналов (например, широкополосные сигналы типа кода Баркера; б) создание устройств для обработки, которые наилучшим образом выделяют сигнал, искаженный присутствием шума.

Частотно-избирательная система, выполняющая обработку суммы сигнала и шума некоторым наилучшим образом, называется оптимальным фильтром. На протяжении длительного периода развития техники связи к частотным фильтрам предъявлялось требование возможно более равномерного пропускания спектра сигнала и более полного подавления частот вне этого спектра. Идеальным считался фильтр с прямоугольной П-образной АЧХ. С развитием теории помехоустойчивости существенно изменились трактовка функций линейного фильтра и подход к его настроению. Фильтр с П-образной АЧХ не является оптимальным в тех случаях, когда имеется априорная информация о форме сигнала и характеристиках помехи. В зависимости от решаемой задачи - 1) обнаружены сигнала, 2) измерение его параметров, 3) разрешение (т.е. различение) сигналов - критерии оптимальности могут быть разными. Для задач обнаружения сигналов заданной (т.е. известной) формы в шумах наибольшее распространение получил критерий максимума отношения сигнал/помеха на выходе фильтра.