Эргодические свойства непериодических цепей.

Стационарное распределение.

Рассмотрим марковскую непериодическую цепь с конечным числом состояний.

Определение 2.9.

Распределение вероятностей { Р_κ} называется стационарным, если

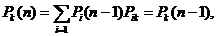( 2.10)

Иными словами, стационарным распределением Р_κ называется распределение инвариантное относительно матрицы преобразований .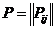

Если начальное распределение {а _κ } стационарно, то абсолютные вероятности { 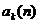} не зависят от времени , т.е. = .

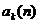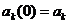Неприводимая цепь Маркова принадлежит к одному из следующих двух классов:

а) или все состояния невозвратные, или все состояния нулевые. В этом случае 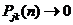при n → 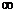для любой пары индексов , и не существует стационарного распределения;

б) или все состояния эргодические, т.е.

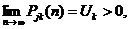(2.11)

где u _к- величина, обратная среднему времени возвращения в состояние R.

В этом случае { u _к } – стационарное распределение и не существует никаких других стационарных распределений.

Докажем теорему о стационарных распределениях марковских цепей.

Теорема 2.3. Если для марковской цепи существует стационарное распределение, то оно единственно и для любого начального распределения

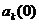{ } справедливо:

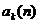
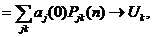(2.12)

в противном случае 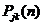→ 0 при n → .

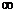Для доказательства заметим, что ∑ 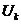≤ 1. Это следует непосредственно из того, что при фиксированных j и n величины:

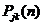, к = 1, 2,… в сумме равны единице, так что u ₁+ u ₂ +…+ u _N ≤ 1 при любых N. Вероятность перехода 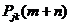, как это было показано в п. 2.2.1, равняется 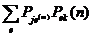. Если n = 1 и m → ∞, то 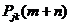стремится к 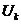, а слагаемые правой части стремятся к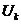 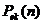. Сложив произвольное количество членов, убеждаемся, что 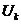≥ 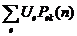. Суммируя эти неравенства по всем R, мы получаем в каждой из частей неравенства конечную величину ∑ 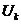_. Это показывает, что знак неравенства невозможен и, таким образом, 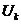= ∑ 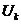Р_{j k} . Положив 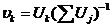, видим, что распределение { 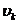} стационарно и, значит, по крайней мере, одно такое распределение существует.

Пусть теперь { 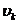} – произвольное распределение, удовлетворяющее (2.10). Умножая это соотношение на 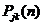и суммируя по всем j , получим по индукции, что при любом n 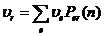. Устремив n к бесконечности, в пределе получим 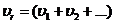, т.е. распределение { 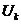} единственно.

Если все состояния или невозвратные, или нулевые, а распределение { 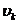} стационарно, то уравнение 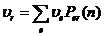по - прежнему имеет место. В то же время 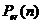→ 0, что, очевидно, невозможно. Поэтому стационарное распределение может существовать только в эргодическом случае, и теорема доказана полностью.

ПУАССОНОВСКИЕ ПРОЦЕССЫ

ПРИМЕРЫ ПУАССОНОВСКИХ ПРОЦЕССОВ В АСУ.

Математической моделью, часто используемой для анализа и интерпретации процессов в АСУ является пуассоновский процесс. К пуассоновским процессам приводят задачи, рассмотренные в следующих примерах.

Пример 3. В таблице 1 приведены данные от отказах электронной вычислительной машины в виде наблюдаемых моментов времени отказов t_1, t_2, . . . , t _n [3]. Другим способом задания такого процесса является построение графика числа накопленных отказов – функции N (t). График для числа накопленных отказов электронной вычислительной машины представлен на рис. 4.

Пример 4.В качестве второго примера рассмотрим вычислительную систему, функционирующую в режиме реального времени. В этой системе задания на обработку поступают в ЭВМ от терминалов по линиям связи от удаленных пользователей. Так как пользователи независимы, они инициируют задания в произвольные моменты времени. Если первое задание пришло в момент t_{1 ,} второе – в момент t₂ и т.д., то этот поток заданий можно описать с помощью функции N (t), соответствующей числу заданий, поступивших к моменту времени t.

Таблица 1.