Свойства непрерывных функций

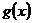1. Если функции и непрерывны в точке , то их сумма 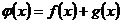также есть непрерывная функция в точке . Это свойство справедливо для любого конечного числа слагаемых.

2. Произведение двух непрерывных функций есть функция непрерывная.

3. Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль.

4. Если функция непрерывна в точке и 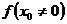, то значения функции в некоторой окрестности точки имеют тот же знак, что и .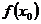

5. Если функция 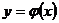непрерывна в точке и принимает в этой точке значение 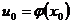, а функция 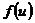непрерывна в точке 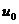, то сложная функция 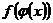непрерывна в точке .

6. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.

7. Если непрерывная на некотором обрезке функция принимает на его концах значение разных знаков, то на этом отрезке найдется хотя бы одна точка, в которой .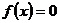

8. Если функция непрерывна в точке , то операция вычисления предела в этой точке и функции переставимы, т.е.

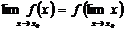(30) На свойстве 8 (равенства (30)) и было основано непосредственное вычисление предела функции в случае отсутствия неопределенности (см.параграфы 16.1 – 16.4).

Если нарушается хотя бы одно условие, указанное в определении непрерывности, то называется такой разрыв функции.

Классификацию точек разрыва дают в зависимости от того, какое условие последнего определения непрерывности (в том числе равенства (29)) нарушено.

Точки разрыва I рода

1. Если существуют односторонние пределы в точке (конечные) и

,

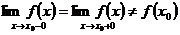то называется точкой устранимого разрыва.

2. Если существует односторонние пределы в точке (конечные) и 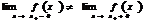, (44)

то - точка разрыва, который называется скачок.

В случае устранимого разрыва функцию можно доопределить в точке значением и она станет непрерывной.

В случае скачка сделать это невозможно.

Точки разрыва II рода

1. Ес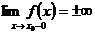ли

или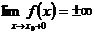

то – точка разрыва, который называется бесконечный скачок. В этом случае прямая 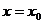является вертикальной асимптотой.

2. Если односторонние пределы в точке не существуют (не определены), то - точка неопределенности.

Получили, что 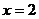– точка разрыва I рода (скачка). Значит, функция непрерывна всюду на числовой прямой кроме точки 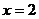, в которой она имеет скачок, равный 1.

В41.Дифференцирование функции с переменной в основании степени и в показателе

Производная функции

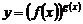, (1)

где 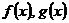– некоторые выражения с переменной x, не может быть вычислена по табличным формулам дифференцирования степенной функции и показательной функции (так как переменная находится как в основании степени, так и в её показателе). Заданная функция типа (1) называется показательно-степенной.

Способы вычисления производной показательно-степенной функции

Первый способ вычисления

Используют метод логарифмического дифференцирования. Для этого:

1) логарифмируют обе части уравнения, которым задается функция (например, по основанию ):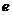

,

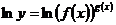получают

;

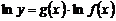2) дифференцируют обе части полученного равенства, где считают 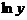сложной функцией от 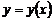(правую часть равенства дифференцируют как произведение функций):

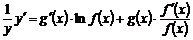
3) выражают из полученного равенства :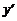

;

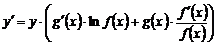4) заменяют y его выражением через x:

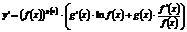. (2)

При решении данным методом используют не конечную формулу (2), а реализуют процесс логарифмического дифференцирования для каждой функции типа (1).

Второй способ

На основании свойства логарифмов записывают

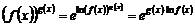. (3)

Далее дифференцируют как сложную функцию.

С помощью логарифмического дифференцирования удобно также вычислять производные функций при наличии в их аналитическом задании большого количества операций умножения, деления, возведения в степень.