Теоремы Ролля, Коши, Лагранжа (доказательство одной из них).

Теорема Ролля. Если функция 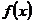непрерывна ,на отрезке , и дифференцируема в промежутке и принимает на концах отрезка равные значения , то в промежутке найдется по крайней мере одна такая точка 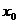, в которой производная будет равна нулю: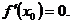

Теорема Коши. Если две функци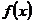и и 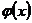непрерывны на отрезке и дифференцируемы в промежутке , причем производная второй из них 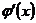не обращается в нуль в этом промежутке, то отношение конечных приращений этих функ­ций на отрезке равно отно­шению их производных в некоторой точке с промежутка , быть может, не единственной: 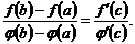(5.7)

Заметим, что 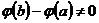, так как иначе по теореме Ролля произ­водная 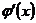обращалась бы в нуль хотя бы в одной точке промежутка , а по условию теоремы Коши 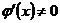в этом промежутке.

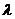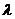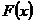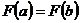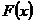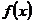Доказательство. Введем вспомогательную функцию , где — неопределенный пока постоянный множитель, и выберем так, чтобы функция удовлетворяла на отрезке всем условиям теоремы Ролля. Для этого нам достаточно потребовать, чтобы , так как остальным условиям теоремы Ролля функция удов­летворяет: она непрерывна на отрезке и дифференцируема в проме­жутке , так как этими свойствами обладают обе функции и .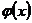

Итак, потребуем, чтобы 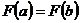или чтобы . Это дает для множителя 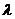конечное значение:

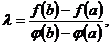(5.8) поскольку .

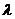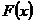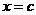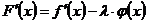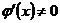При таком значении функция будет удовлетворять всем условиям теоремы Ролля. Поэтому ее производная обратится в нуль по крайней мере в одной точке промежутка : ; или, так как , то . По условию теоремы [ в промежутке ]. Поэтому из предыдущего равенства найдем (5.9)

Сравнивая правые части равенств (5.8) и (5.9), определяющих одно и то же число 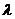, получим равенство (14.7). Теорема Коши доказана.

Теорему Лагранжа получим, положив , в силу чего 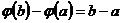, 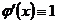и .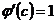

Внося эти-значения в равенство (5.7), получаем 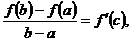(5.10) или 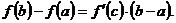(5.11)

Полученная формула (5.11) называется формулой Лагранжа, и опре­деляет содержание теоремы Лагранжа: конечное приращение на отрезке функции, непрерывной на этом отрезке и дифференцируемой внутри него, равно произведению конечного приращения аргумента на этом отрезке на значение производной в некоторой внутренней точке отрезка .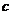

Геометрический смысл теоремы Лагранжа определяется формулой (5.10). В ней левая часть равна угловому коэффициенту уравнения хорды 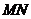, соединяющей точки и 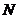графика функции 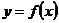(см. рис. 5.18):

Правая часть этой формулы 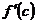равна угловому коэффициенту касательной к этому графику в точке 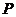с абсциссой 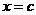, где (рис. 5.18):

Формула (5.10) устанавливает ра­венство этих угловых коэффициентов, т. е. параллельность хорды и касатель­ной. Таким образом, геометрический смысл теоремы Лагранжа следующий: На произвольной дуге графика диф­ференцируемой функции всегда найдется такая точка, в которой касательная к графику будет параллельна хорде, стягивающей концы дуги.

Тот же геометрический смысл имеет и теорема Коши, если рассматри­вать функции и 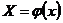как параметрические уравнения некоторой кривой на плоскости , а 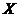при этом считать параметром этой кривой.

Правило Лопиталя.

Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле.

Итак, если имеется неопределенность вида (1)

Доказательство.

Рассмотрим доказательство теоремы для неопределенности вида при . Предположим, что функции f(x) и g(x), а также их производные непрерывны в точке x₀, причем и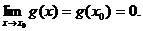

В этом случае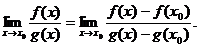

Применяя теорему Лагранжа для функций f(x) и g(x) на отрезке 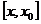, получим 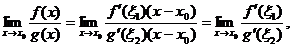где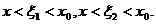

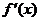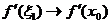При в силу непрерывности производных и имеем и