Дифференциал: определение, геометрический и физический смысл.
Дифференциалом функции называется главная, линейная относительно 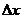 часть приращения функции, равная произведению производной на приращение независимой переменной:
часть приращения функции, равная произведению производной на приращение независимой переменной: 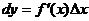 .
.
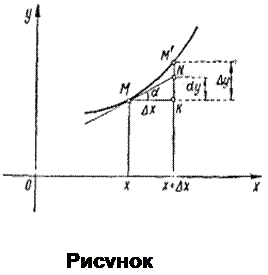
Дифференциал функции имеет простой геометрический смысл: значение дифференциала функции, при данном значении аргумента 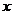 и данном приращении
и данном приращении 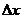 , равно приращению ординаты касательной,, проведенной в точке с абсциссой
, равно приращению ординаты касательной,, проведенной в точке с абсциссой 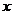 графика этой функции, при переходе от точки касания (с абсциссой
графика этой функции, при переходе от точки касания (с абсциссой 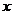 ) к соседней точке касательной с абсциссой
) к соседней точке касательной с абсциссой 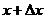 .
.
В самом деле, соответствующее приращение ординаты касательной на рис. 4.5 изображается катетом KN треугольника MKN, в котором вторым катетом служит отрезок МК= 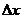 , а острый угол при вершине М равен
, а острый угол при вершине М равен 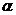 , причем
, причем 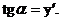 Но тогда KN = МК
Но тогда KN = МК 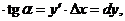 что и требовалось доказать.
что и требовалось доказать.
Отметим одно характерное свойство дифференциала функции: дифференциал сложной функции, т. е. функции, зависящей от аргумента 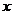 через промежуточный аргумент
через промежуточный аргумент 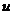 , все же равен, как и в случае простой функции (см. 4.64*), произведению производной от этой функции по промежуточному аргументу на дифференциал этого аргумента. Таким образом, если
, все же равен, как и в случае простой функции (см. 4.64*), произведению производной от этой функции по промежуточному аргументу на дифференциал этого аргумента. Таким образом, если 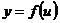 , где
, где 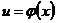 , то
, то 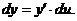 (4.67) В самом деле, по правилу дифференцирования сложной функции имеем
(4.67) В самом деле, по правилу дифференцирования сложной функции имеем 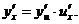 Отсюда, умножая на
Отсюда, умножая на 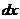 , находим
, находим 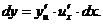 Но
Но 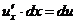 и, следовательно,
и, следовательно, 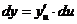 , что и требовалось доказать. Это свойство дифференциала называют свойством инвариантности, т. е. свойством неизменности формы записи дифференциала функции, как в случае простой, так и в случае сложной функции. [Производная, как нам известно, свойством инвариантности не обладает: § 3, (4.21).]
, что и требовалось доказать. Это свойство дифференциала называют свойством инвариантности, т. е. свойством неизменности формы записи дифференциала функции, как в случае простой, так и в случае сложной функции. [Производная, как нам известно, свойством инвариантности не обладает: § 3, (4.21).]
| I. Правила дифференцирования | II. Формулы дифференцирования |
1. 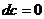 2. 2. 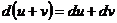 3. 3. 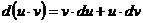 4. 4. 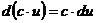 5. 5. 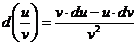 | 1. 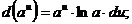 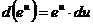 2. 2. 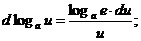 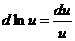 3. 3. 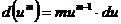 4. 4. 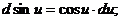 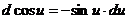 5. 5. 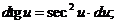 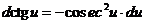 6. 6. 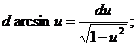 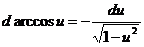 7. 7. 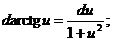 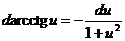 |
30. Производные и дифференциалы второго порядка: определения и методы их вычисления.
Производную от производной данной функции, если она существует, называют производной второго порядка, или второй производной, от данной функции и обозначают символом 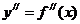 . Таким образом
. Таким образом
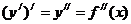 (4.56). В связи с этим производную
(4.56). В связи с этим производную 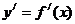 в дальнейшем будем называть производной первого порядка, или первой производной.
в дальнейшем будем называть производной первого порядка, или первой производной.
Рассмотрим несколько примеров отыскания производных высших порядков.
1. Найти производную 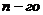 порядка от функции
порядка от функции 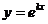 .
.
Находим, выполняя последовательные дифференцирования: 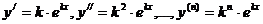 .
.
2. Найти производную 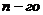 порядка от функций
порядка от функций 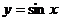 и
и 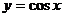 .
.
Первую производную от 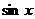 , равную
, равную 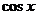 , можно записать в следующем виде:
, можно записать в следующем виде:
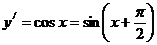 отсюда следует, что операция дифференцирования функции
отсюда следует, что операция дифференцирования функции 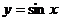 по
по 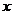 формально сводится к прибавлению
формально сводится к прибавлению 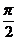 к аргументу синуса. В силу этого
к аргументу синуса. В силу этого 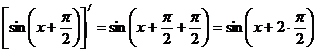 ; поэтому
; поэтому 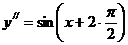 . Аналогично,
. Аналогично, 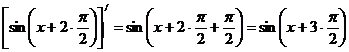 ; поэтому
; поэтому 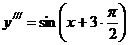 и вообще
и вообще
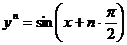 . Аналогично можно убедиться в том, что если
. Аналогично можно убедиться в том, что если 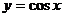 , то
, то 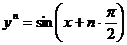 .
.
3. Найти производную 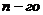 порядка от функции
порядка от функции 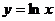 . Имеем
. Имеем 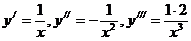 ,
,
откуда, заметив общий закон образования последовательных производных, находим 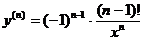 .
.
4. Найти производную 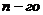 порядка от функции
порядка от функции 
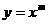 (
( 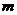 - любое действительное число).
- любое действительное число).
Имеем последовательно 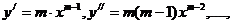 откуда, заметив общий закон образования производных, находим
откуда, заметив общий закон образования производных, находим 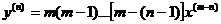
В частном случае, когда 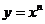 (
( 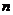 - целое положительное число),
- целое положительное число), 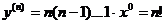 . Все же дальнейшие производные от
. Все же дальнейшие производные от 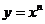 будут равны нулю, как производные от постоянного.
будут равны нулю, как производные от постоянного.
Отсюда следует, что если целая рациональная функция степени 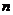 от
от 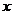 (многочлен степени
(многочлен степени 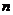 относительно
относительно 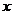 ):
):
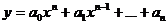 ,
,
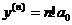 , а
, а 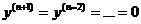 .
.
Дифференциалом второго порядка (его обозначают символом 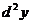 ) от функции
) от функции 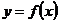 называют дифференциал ее дифференциала:
называют дифференциал ее дифференциала: 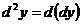 (4.69)
(4.69)
Найдем его выражение. Имеем 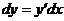 , причем
, причем 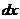 — произвольное приращение аргумента
— произвольное приращение аргумента 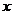 , которое от аргумента
, которое от аргумента 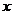 не зависит. В виду этого при отыскании второго дифференциала функции надо рассматривать дифференциал
не зависит. В виду этого при отыскании второго дифференциала функции надо рассматривать дифференциал 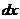 независимого переменного как величину постоянную относительно аргумента
независимого переменного как величину постоянную относительно аргумента 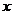 .
.
Находим 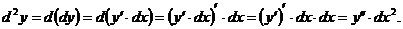
Таким образом, второй дифференциал функции равен произведению ее второй производной на квадрат дифференциала независимого переменного: 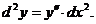
Если дифференциал 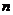 -го порядка (обозначение
-го порядка (обозначение 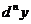 ) уже введен, то дифференциалом
) уже введен, то дифференциалом 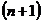 -го порядка будет дифференциал дифференциала
-го порядка будет дифференциал дифференциала 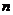 -го порядка:
-го порядка: 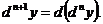
Докажем методом индукции справедливость следующей формулы:
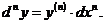 (4. 72)
(4. 72)
Исходя из формулы (4.72), найдем 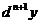 , как дифференциал от
, как дифференциал от 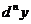 :
:
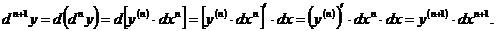
Поскольку для 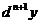 получено такое же выражение, как и для
получено такое же выражение, как и для 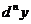 , можно утверждать, что формула (4.72) справедлива при всяком
, можно утверждать, что формула (4.72) справедлива при всяком 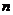 , так как при
, так как при 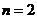 она доказана [см. (4.70)]. Из формулы (4.72) получим выражение для производной
она доказана [см. (4.70)]. Из формулы (4.72) получим выражение для производной 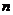 -го порядка через отношение дифференциалов:
-го порядка через отношение дифференциалов: 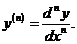 (4.73)
(4.73)
Таким обозначением производных 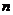 -го порядка в анализе часто пользуются наряду с обозначениями
-го порядка в анализе часто пользуются наряду с обозначениями 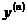 и
и 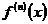 .
.
Дифференциалы высших порядков, начиная со второго, вообще говоря, не обладают свойством инвариантности: структура дифференциала сложной функции иная, чем дифференциала функции простой.
Убедимся в этом на примере дифференциала второго порядка. Пусть 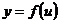 ,
, 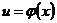 . В силу инвариантности первого дифференциала
. В силу инвариантности первого дифференциала 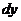 , имеем:
, имеем: 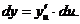
Но так как 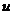 — функция от
— функция от 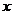 , то
, то 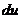 уже не будет величиной постоянной относительно
уже не будет величиной постоянной относительно 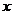 . Поэтому дифференциал от
. Поэтому дифференциал от 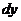 надо искать как дифференциал произведения:
надо искать как дифференциал произведения:
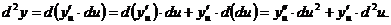
Таким образом, уже в выражении второго дифференциала сложной функции появляется дополнительное слагаемое 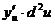 , зависящее от второго дифференциала промежуточного аргумента. Это же будет иметь место и для дифференциалов более высоких порядков. Тем самым в общем случае утверждение наше доказано.
, зависящее от второго дифференциала промежуточного аргумента. Это же будет иметь место и для дифференциалов более высоких порядков. Тем самым в общем случае утверждение наше доказано.
Примечание. Свойство инвариантности у дифференциалов второго и высших порядков сохраняется лишь тогда, когда промежуточный аргумент 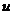 является линейной функцией независимого переменного
является линейной функцией независимого переменного  :
: