Разложение ф-ции в тригонометрический ряд

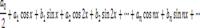
Тригонометрический ряд

Достаточное условие разрешимости этой задачи состоит в том, чтобы функция была в интервале [-π, π]и сумма ряда, если он сходится, также является периодической функцией с периодом 2п.Допустим, что функция f(x)есть сумма этого ряда

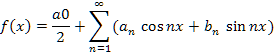
В таком случаи говорят, что функция разгалается в тригонометрический ряд

17 Биномиальный ряд Биномиальный ряд, бесконечный ряд, являющийся обобщением формулы Ньютона бинома (1 + х) n на случай дробных и отрицательных показателей n:

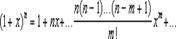
Биномиальный ряд сходится: при —1 < x <1, если n < —1; при —1< x £ 1, если —1 < n < 0; при —1 £ x £ 1, если n > 0.

18 Принцип Даламбера Признак Даламбера

Если для числового ряда

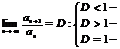1сходится,2 расходится, 3- нужны допол. исследование

19 Числовые ряды необ.и дост. Признаки сходимости Ряды с произвольными членами.

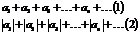Если (2) сходятся: (1) – абсолютно сходящийся (2) расход., (1) – сход.: (1) – условно сходящийся

Теорема об абсолютной сходимости:

Если (2) – сходится, то (1) – тоже сходится (обратное неверно)

Ряд сходится, если S конечно; тогда

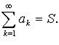
Необходимое условие сходимости ряда:

Д.У. консольной балки

Изгиб. Момнет М=М1+М2

М1-собст вес, М2-внешн. Силы,М-?

Для определения М надо вычислить элемент.∆М1

∆М1=∆tgt; М1≈∑∆М1

М1∫ qtdt=q*t*t/2=q/2(l-x*x)

∑M=EJ/R

E-модуль Юнга J-момент инерции попереч. сечения балки

R-радиус кривизны балки

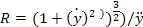
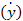=tgα α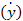=0 =0

R=1/y^4 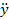=1/ EJ-ДУ

Д.У равномерно нагруженной консольной балки

Теоремы о сравнении числовых рядов

Признак сравнения

Если 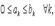то из сходимости ряда

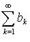следует сходимость ряда 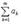а из расходимости ряда 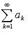расходимость ряда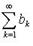

Предельный признак сравнения

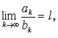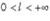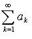Если то при ряды и 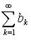или оба сходятся, или оба расходятся; при

l = 0 из сходимости ряда следует сходимость ряда ; при из расходимости ряда 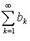следует расходимость ряда 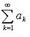. В частности, если при 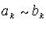то ряды 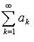и и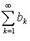ли оба сходятся, или оба расходятся.

Д.У. консольной балки со сосредоточенной нагрузкой (на концах)

Разложение в ряд Фурье на(-l;l)

Интегральный признак Коши сход.рядов

Если 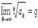то при 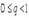ряд 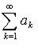сходится, при q > 1 расходится

Если f убывает на 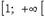и неотрицательна, то ряд 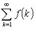сходится или расходится вместе с интегралом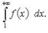

26.Четно е и нечетное разложение в ряд Фурье функции [0,п]

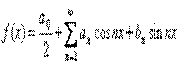
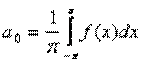
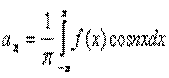
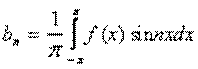
Оценка погрешности при вычислении определенного интеграла по формуле трапеций

Если функция f(x) имеет на [а,б] непрерывную вторую производную f’’(x) b M≥{f’’(x) на отрезке [а,б], то погрешность приближения e можно вычислить с помощью формулы:

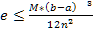
Решение ур-ий методом итераций. Условие сходимости

Уравнение f(x)=0 преобразуют к виду x=фx таким образом, что бы неравенство ф’(x)<1 выполнялось для всех х на отрезке а,б Это легко сделать, если f’(x) сохраняет знак на а,б. В этом случае берут число М, М≥max[f’(x)]на отрезке а,б и полагают

Λ=-I/M при [f’(x)]на отрезке а,б.>0 или Λ=-1/M

При max[f’(x)]на отрезке а,б<0/Далее преобразуют уравнение f(x)=0 к виду x=x+λ*f(x). Если f(x) не сохраняет знак на отрезке, то можно уменьшить отрезок изоляции корня и проверить требования сохранения знака f’(x) уже на новом отрезке