Свойства непрерывных функций.

Операции над векторами

Пусть векторы и принадлежат n-мерному векторному пространству Rⁿ:

Будем называть суммой векторов и вектор , координа­ты которого равны суммам соответствующих координат этих векторов:

Пусть λ — любое действительное число. Произведением вектора на число λ будем называть вектор, координаты ко­торого получаются умножением соответствующих координат вектора на это число:

Из введенных таким образом операций над векторами вы­текают следующие свойства этих операций. Пусть , и — произвольные векторы n-мерного векторного пространства. Тогда:

1) + = + — переместительное свойство;

2) ( + ) + = + ( + ) — сочетательное свойство;

3) λ( + ) = λ + λ , где λ — действительное число;

4) (λ + μ) = λ + μ , где λ и μ — действительные числа;

5) λ(μ ) = (λμ) , где λ и μ — действительные числа;

6) + = ;

7) для любого вектора существует такой вектор - , что - = (-1) , + (- ) = ;

8) 0 = для любого вектора .

47. Скалярное произведение векторов. Свойства скалярного произведения векторов.

Скалярным произведением векторов (12.3) называется число, состоящее из суммы произведений соответ­ствующих координат этих векторов:

Как мы видим, формально такое определение скалярного произведения двух векторов согласуется с аналогичным опре­делением двух- и трехмерных векторов. Из данного определе­ния следуют основные свойства скалярного произведения век­торов:

1) = ;

2) (λ ) = (λ ) = λ( ), где λ — действительное число;

3) ( + ) = + ;

4) > 0, если ≠ , и = 0, если = .

Введем понятие модуля вектора (его длины) и угла между векторами в виде обобщения на случай п > 3.

48. Ортогональные векторы.

. Векторы и бу­дем называть ортогональными, если их скалярное произведе­ние равно нулю:

Равенство (12.5) является аналогом условия перпендику­лярности векторов в двух- и трехмерном случаях, когда в ра­венстве (12.4) cosφ = 0.

49. Линейная комбинация и линейная зависимость векторов.

Линейной комбинацией векторов (12.6) назы­вается вектор вида

где λ₁, λ₂, ..., λ_k — любые действительные числа.

Например, пусть даны три вектора: ₁ = (1, 2, 0), ₂ = (2, 1, 1) и ₃ = (-1, 1, -2). Их линейной комбинацией с коэффициентами соответственно 2, 3 и 4 является вектор = (4, 11, -5).

В случае равенства (12.7) говорят также, что вектор ли­нейно выражается через векторы (12.6) или разлагается по этим векторам.

Система ненулевых векторов (12.6) называ­ется линейно зависимой, если существуют такие числа λ₁, λ₂, ..., λ_k, не равные одновременно нулю, что линейная комбина­ция данной системы с указанными числами равна нулевому вектору:

Например, система двух векторов ₁ = (1, 0) и ₂ = (0, 2) является линейно независимой; система двух векторов ₁ = (1, 2, 1) и ₂ = (2, 4, 2) является линейно зависимой, так как ₂ — 2 ₁ = .

50. п – мерное линейное векторное пространство. Метрика линейного пространства.

Векторное пространство называется n-мepным (или имеет «размерность n»), если в нём существуют n линейно независимых элементов e₁, e₂,..., e_n, а любые n + 1 элементов линейно зависимы (обобщённое условие В). Векторное пространство называются бесконечномерным, если в нём для любого натурального n существует n линейно независимых векторов. Любые n линейно независимых векторов n-мepного Векторное пространство образуют базис этого пространства. Если e₁, e₂,..., e_n — базис Векторное пространство, то любой вектор хэтого пространства может быть представлен единственным образом в виде линейной комбинации базисных векторов:

x = a₁e₁ + a₂e₂ +... + a_ne_n.

При этом числа a₁, a_2,..., a_n называются координатами вектора х в данном базисе.

51. Размерность и базис линейного пространства. Разложение вектора по базису. Единичный базис.

Векторное пространство называется n-мepным (или имеет «размерность n»), если в нём существуют n линейно независимых элементов e₁, e₂,..., e_n, а любые n + 1 элементов линейно зависимы

Рассмотрим систему векторов

Максимально независимой подсистемой этой системы векто­ров называется частичный набор векторов системы, удовле­творяющий двум условиям: а) векторы этого набора линейно независимы, б) любой вектор системы линейно выражается че­рез векторы этого набора.

Справедлива теорема, утверждающая, что все максималь­но независимые подсистемы данной системы векторов содер­жат одно и то же число векторов. Максимально независимая подсистема системы векторов называется ее базисом; векторы, входящие в базис, называются базисными векторами. Будем называть рангом системы векторов число векторов ее базиса. Понятно, что если ранг системы векторов меньше числа k ее векторов, то она может иметь несколько базисов.

Понятие базиса распространяется и на пространство Rⁿ, которое является системой, содержащей всю бесконечную со­вокупность n-мерных векторов.

Определение 3. Система n векторов называется базисом про­странства Rⁿ,если:

1) векторы этой системы линейно независимы;

2) всякий вектор из Rⁿ линейно выражается через векторы данной системы.

Разложение любого вектора в базисе, если оно существует, является единственным.

52. Евклидово векторное пространство.

Определение 2. Евклидовым векторным пространством²⁾ называется векторное пространство над полем с фиксированным скалярным произведением .

Пример 3. Пространство является евклидовым пространством. Скалярное произведение здесь можно задать формулой из примера 2.

Определение 3. Пусть — евклидово пространство. Для любого число называется длиной, или нормой вектора .

53. Решение системы линейных уравнений методом Жордана-Гаусса.

Рассмотрим систему уравнений общего вида (15.1). Пусть для определенности a₁₁ ≠ 0 (если a₁₁ = 0, то можно переста­вить на первое место ненулевое слагаемое или начать с другого уравнения). Умножим первое уравнение системы (15.1) на чис­ло a₂₁/a₁₁ и затем вычтем его из второго уравнения этой системы. Умножим обе части первого уравнения на число a₃₁/a₁₁ и затем вычтем его из третьего уравнения и так далее, т.е. процесс заключается в последовательном вычитании первого уравнения, умножаемого на числа a_i1/a₁₁, из i-го уравнения (i = 2, 3, ... , m). Таким образом, в результате элементарных преобразований мы получим эквивалентную систему, в кото­рой начиная со второго уравнения отсутствуют слагаемые, со­держащие неизвестное x₁:

где верхний индекс в скобках означает новые коэффициенты, полученные после первого шага. Для удобства записи будем оперировать расширенной матрицей системы, отделяя в ней вертикальной чертой столбец свободных членов. Итак, после первого шага, содержащего (т — 1) элементарных преобразо­ваний системы, мы переходим от расширенной матрицы (15.4) исходной системы к расширенной матрице

Второй шаг заключается в том, что теперь второе уравне­ние системы (15.7) или вторая строка матрицы (15.8) исполь­зуется для аналогичных элементарных преобразований строк с третьей по m-ю: эта строка последовательно умножается на число и вычитается из i-й строки (i = 3, 4, ... ,m). В результате этих (m - 2) элементарных преобразований полу­чаем новую расширенную матрицу, соответствующую новой эквивалентной системе уравнений. Эта матрица имеет вид

где верхний индекс означает новые коэффициенты. В случае если элемент = 0, то второе уравнение можно поменять местами с другим уравнением, у которого элемент ≠ 0.

Продолжим этот процесс аналогичным образом (т.е. на 3-м шаге преобразуются строки с 4-й по т-ю, на 4-м шаге — стро­ки с 5-й по m-ю и т.д.) до тех пор, пока не дойдем до последней m-й строки. После (r - 1)-го шага процесса последовательного исключения неизвестных мы получим следующую расширен­ную матрицу:

Последние (m - r) строк этой матрицы соответствуют урав­нениям эквивалентной системы уравнений

Эти уравнения могут появиться, если соответствующие урав­нения исходной системы (15.1) представляют собой линейные комбинации других уравнений этой системы, о чем говорилось в п. 15.1. Здесь мы не исследовали заранее систему (15.1) на совместность; поэтому если эта система несовместна, то хотя бы одно из чисел , ,..., не равно нулю. Таким образом, метод Гаусса позволяет на определенном шаге устано­вить возможную несовместность исходной системы линейных уравнений или выявить и удалить уравнения, являющиеся ли­нейными комбинациями других уравнений системы (15.1), если она совместна.

54. Определение матрицы. Линейные операции над матрицами, свойства этих операций.

Определение 1. Прямоугольная таблица чисел вида

называется матрицей. Здесь a_ij — действительные числа (i = 1, 2,..., m, j = 1, 2, ..., n), называемые элементами матрицы, i и j — соответственно индексы строки и столбца. При этом произведение m х n числа строк на число столбцов называют размером матрицы А. Часто матрицу (13.1) запи­сывают в сокращенном виде:

Матрица, все элементы которой равны нулю, называется нулевой матрицей.

В том случае, когда m = n (число строк равно числу столб­цов):

матрица А называется квадратной.

Упорядоченная совокупность элементов a₁₁, a₂₂,. …, а_пп на­зывается главной диагональю квадратной матрицы. Квадрат­ная матрица называется диагональной, если ее элементы удов­летворяют условию

т.е. ненулевыми могут быть только элементы главной диагонали; матрица в этом случае имеет вид

Единичной матрицей называется диагональная матрица, у которой все элементы главной диагонали равны единице:

Определение 2. Две матрицы А и В называются равными (А = В), если они имеют одинаковые размеры и их соответ­ствующие элементы равны: a_ij = b_ij , i = 1, 2,..., m, j = 1, 2, .... n.

Уравнение прямой в отрезках

Прямая линия, пересекающая ось Ox в точке и ось Oy в точке :

В этом виде невозможно представить прямую, проходящую через начало координат.

Общее уравнение плоскости

ax + by + cz + d = 0;

если а = 0, плоскость параллельна прямой Ох;

если b = 0, плоскость параллельна прямой Оy;

если c = 0, плоскость параллельна прямой Oz;

если d = 0, плоскость проходит через начало координат;

если a = b = 0, плоскость параллельна плоскости xОy;

если a = c = 0, плоскость параллельна плоскости xОz;

если b = c = 0, плоскость параллельна плоскости yОz;

Уравнение плоскости в отрезках:

а, b, с — отрезки, отсекаемые плоскостью на осях;

Уравнение прямой, проходящей через точку А(х₀; у₀; z₀) перпендикулярно вектору :

а(х – х₀) + b(у – у₀) + с (z – z₀) = 0

Угол между плоскостями
а₁х + b₁y + c₁z + d₁ = 0 и а₂х + b₂y + c₂z + d₂ = 0

Обоснование

Нижеприведенное обоснование метода множителей Лагранжа не является его строгим доказательством. Оно содержит эвристические рассуждения, помогающие понять геометрический смысл метода.

Двумерный случай

Линии уровня 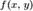и кривая .

Пусть требуется найти экстремум некоторой функции двух переменных 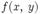при условии, задаваемом уравнением 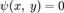. Мы будем считать, что все функции непрерывно дифференцируемы, и данное уравнение задает гладкую кривую S на плоскости 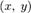. Тогда задача сводится к нахождению экстремума функции f на кривой S. Будем также считать, что S не проходит через точки, в которых градиент f обращается в 0.

Нарисуем на плоскости 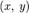линии уровня функции f (то есть кривые 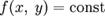). Из геометрических соображений видно, что экстремумом функции f на кривой S могут быть только точки, в которых касательные к S и соответствующей линии уровня совпадают. Действительно, если кривая S пересекает линию уровня f в точке 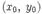трансверсально (то есть под некоторым ненулевым углом), то двигаясь по кривой S из точки 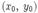мы можем попасть как на линии уровня, соответствующие большему значению f, так и меньшему. Следовательно, такая точка не может быть точкой экстремума.

Тем самым, необходимым условием экстремума в нашем случае будет совпадение касательных. Чтобы записать его в аналитической форме, заметим, что оно эквивалентно параллельности градиентов функций f и ψ в данной точке, поскольку вектор градиента перпендикулярен касательной к линии уровня. Это условие выражается в следующей форме:

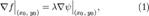
где λ — некоторое число, отличное от нуля, и являющееся множителем Лагранжа.

Рассмотрим теперь функцию Лагранжа , зависящую от и λ:

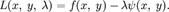
Необходимым условием ее экстремума является равенство нулю градиента 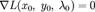. В соответствии с правилами дифференцирования, оно записывается в виде

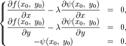
Мы получили систему, первые два уравнения которой эквивалентны необходимому условию локального экстремума (1), а третье — уравнению 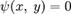. Из нее можно найти 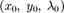. При этом 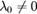, поскольку в противном случае градиент функции f обращается в нуль в точке , что противоречит нашим предположениям. Следует заметить, что найденные таким образом точки 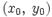могут и не являться искомыми точками условного экстремума — рассмотренное условие носит необходимый, но не достаточный характер. Нахождение условного экстремума с помощью вспомогательной функции L и составляет основу метода множителей Лагранжа, примененного здесь для простейшего случая двух переменных. Оказывается, вышеприведенные рассуждения обобщаются на случай произвольного числа переменных и уравнений, задающих условия.

78. Общая задача линейного программирования. Геометрическая интерпретация задачи.

Линейное программирование – это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения. Таким образом, задачи линейного программирования относятся к задачам на условный экстремум функции. Казалось бы, что для исследования линейной функции многих переменных на условный экстремум достаточно применить хорошо разработанные методы математического анализа, однако невозможность их использования можно довольно просто проиллюстрировать

Действительно, путь необходимо исследовать на экстремум линейную функцию Z = С ₁ х ₁ +С ₂ х ₂ +… +С _N x _N

при линейных ограничениях

a ₁₁ x ₁ + a ₂₂ x ₂ + … + a _1N Х _N = b ₁

a ₂₁ x ₁ + a ₂₂ x ₂ + … + a _2N Х _N = b ₂

. . . . . . . . . . .

a _М1 x ₁ + a _М2 x ₂ + … + a _МN Х _N = b _М

Так как Z – линейная функция, то = С _j (j = 1, 2, …, n), то все коэффициенты линейной функции не могут быть равны нулю, следовательно, внутри области, образованной системой ограничений, экстремальные точки не существуют. Они могут быть на границе области, но исследовать точки границы невозможно, поскольку частные производные являются константами

Для решения задач линейного программирования потребовалось создание специальных методов. Особенно широкое распространение линейное программирование получило в экономике, так как исследование зависимостей между величинами, встречающимися во многих экономических задачах, приводит к линейной функции с линейными ограничениями, наложенными на неизвестные

1. Общая задача линейного программирования

1. Формулировка задачи.

Даны линейная функция

(1.1) Z = С ₁ х ₁ +С ₂ х ₂ +… +С _N x _N

и система линейных ограничений

a ₁₁ x ₁ + a ₂₂ x ₂ + … + a _1N Х _N = b ₁

a ₂₁ x ₁ + a ₂₂ x ₂ + … + a _2N Х _N = b ₂

. . . . . . . . . . .

a _i1 x ₁ + a _i2 x ₂ + … + a _iN Х _N = b _i (1.2)

. . . . . . . . . . .

a _M1 x ₁ + a _M2 x ₂ + … + a _MN Х _N = b _M

(1.3) x _j 0 (j = 1, 2, … ,n)

где а _ij , Ь _j и С _j - заданные постоянные величины

Найти такие неотрицательные значения х ₁ , х ₂ , …, х _n , которые удовлетворяют системе ограничений (1.2) и доставляют линейной функции (1.1)минимальное значение

Алгоритм решения задач

1. Находим область допустимых решений системы ограни­чений задачи.

2. Строим вектор .

3. Проводим линию уровня L₀, которая перпендикулярна .

4. Линию уровня перемещаем по направлению вектора для задач на максимум и в направлении, противоположном , для задач на минимум.

Перемещение линии уровня производится до тех пор, пока у нее не окажется только одна общая точка с областью допусти­мых решений. Эта точка, определяющая единственное решение задачи ЛП, и будет точкой экстремума.

Если окажется, что линия уровня параллельна одной из сторон ОДР, то в таком случае экстремум достигается во всех точках соответствующей стороны, а задача ЛП будет иметь бесчисленное множество решений. Говорят, что такая задача ЛП имеет альтернативный оптимум, и ее решение находится по формуле

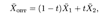
где 0 ≤ t ≤ 1, ₁ и ₂ — оптимальные решения в угловых точках ОДР.

Задача ЛП может быть неразрешима, когда определяющие ее ограничения окажутся противоречивыми.

5. Находим координаты точки экстремума и значение це­левой функции в ней.

80. Решение задачи линейного программирования симплекс-методом. Симплексные таблицы. Алгоритм симплекс-метода.

Метод является универсальным, так как позволяет решить практически любую задачу линейного программирования, за­писанную в каноническом виде.

Идея симплексного метода (метода последовательного улуч­шения плана) заключается в том, что начиная с некоторого исходного опорного решения осуществляется последовательно направленное перемещение по опорным решениям задачи к оп­тимальному. Значение целевой функции при этом перемеще­нии для задач на максимум не убывает. Так как число опорных решений конечно, то через конечное число шагов получим оп­тимальное опорное решение. Опорным решением называется базисное неотрицательное решение.

Полная группа событий

ТЕОРЕМА 2. Сумма вероятностей событий, образующих полную группу, равна единице:

Пример 2. На складе готовой продукции находятся изделия, среди которых 5% нестандартных. Найти вероятность того, что при выдаче изделия со склада оно будет стандартным.

Решение. Вероятность получения нестандартного изделия равна 0,05; события выдачи стандартного и нестандартного из­делия образуют полную группу. Следовательно, сумма их ве­роятностей равна единице, и тогда искомая вероятность рав­на 0,95.

Противоположные события

Определение 2. Два единственно возможных события, обра­зующих полную группу, называются противоположными.

Если событие обозначено через А, то противоположное ему событие обозначается через . Из теоремы 17.2 следует, что

Например, если при стрельбе по мишени попадание — это событие А, то событие — это промах; сумма их вероятностей равна единице — при выстреле обязательно будет либо попа­дание, либо промах. То же самое и при подбрасывании монеты: обязательно выпадет либо орел, либо решка.

Пример 3. В магазине имеется 10 телевизоров, из которых 2 неисправных. Найти вероятность того, что среди наугад взя­тых 3-х телевизоров будет хотя бы один неисправный.

Решение. События "среди взятых телевизоров нет ни од­ного неисправного" и "есть хотя бы один неисправный" — про­тивоположные. Первое из них обозначим через А, а второе — через . Общее число способов, которыми можно взять 3 изде­лия из десяти, равно C . Число исправных телевизоров равно 8, число способов выборки из них трех изделий равно C , так что вероятность Р(А) = C /С . Искомая вероятность опреде­ляется из формулы (17.4):

89. Классическое определение вероятности. Простейшие свойства вероятности.

Назовем каждый из возможных результатов испытания элементарным событием, или исходом. Те элементарные ис­ходы, которые интересуют нас, называются благоприятными событиями.

Определение 3. Отношение числа благоприятствующих со­бытию А элементарных исходов к общему числу равновозможных несовместных элементарных исходов, образующих полную группу, называется вероятностью события А.

Вероятность события А обозначается Р(А). Понятие веро­ятности является одним из основных в теории вероятностей. Данное выше определение является классическим. Из него вы­текают некоторые свойства.

Свойство 1. Вероятность достоверного события равна единице.

Свойство 2. Вероятность невозможного события равна нулю.

Свойство 3. Вероятность случайного события есть поло­жительное число:

Следовательно, вероятность любого события удовлетворя­ет неравенству

Отметим, что современные курсы теории вероятностей ос­нованы на теоретико-множественном подходе, в котором эле­ментарные события являются точками пространства элемен­тарных событий Ω; при этом событие А отождествляется с подмножеством элементарных исходов, благоприятствующих этому событию, А Ω.

Приведем примеры непосредственного вычисления вероят­ностей.

90. Основные правила комбинаторики. Сочетания, перестановки, размещения

Комбинаторика изучает количество комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. При непосредственном вычислении вероятностей часто используются формулы комбинаторики. Приведем наиболее употребительные из них.

1.Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающимися только порядком их расположения. Число всех возможных перестановок Pn = n!, где n! = 1?2?3 ? n, 0! = 1.

Пример 1. Сколько трехзначных чисел можно составить из цифр 1,2,3, если каждая цифра входит в изображение числа только один раз?

Решение. P3 = 3! = 1?2?3 = 6.
2.Размешениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. An m =n!/(n-m)!

Пример 2. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?

Решение . A 2 6 = 6! ?(6-2)! = 720 / 24 = 30.
3.Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хоты бы одним элементом. Cnm = n!/(m!(n-m)!).

Пример 3. Скольким количеством способов можно выбрать две детали из ящика, содержащего 10 деталей?

Решение. C21 0 =10!/(2! ?8!) = 45.
Подчеркнем что числа размещений, перестановок и сочетаний связаны равенством. Anm = PmCnm

91. Частота и относительная частота появления события в серии испытаний. Стохастическая устойчивость случайного события. Статистическое определение вероятности.

Частоту события часто называют его статистической вероятностью (в отличие от ранее введенной «математической» вероятности).

Условимся обозначать частоту (статистическую вероятность) события знаком . Частота события вычисляется на основании результатов опыта по формуле

, (2.3.1)

где – число появления события ; – общее число произведенных опытов.

При небольшом числе опытов частота события носит в значительной мере случайный характер и может заметно изменяться от одной группы опытов к другой. Например, при каких-то десяти бросаниях монеты вполне возможно, что герб появится только два раза (частота появления герба будет равна 0,2); при других десяти бросаниях мы вполне можем получить 8 гербов (частота 0,8). Однако при увеличении числа опытов частота все более теряет случайный характер; случайные обстоятельства, свойственные каждому отдельному опыту, в массе взаимно погашаются, и частота проявляет тенденцию стабилизироваться, приближаясь с незначительными колебаниями к некоторой средней, постоянной величине. Например, при многократном бросании монеты частота появления герба будет лишь незначительно уклоняться от ½.

Это свойство «устойчивости частот», многократно проверенное экспериментально и подтверждающееся всем опытом практической деятельности человечества, есть одна из наиболее характерных закономерностей, наблюдаемых в случайных явлениях. Математическую формулировку этой закономерности впервые дал Я. Бернулли в своей теореме, которая представляет собой простейшую форму закона больших чисел. Я. Бернулли доказал, что при неограниченном увеличении числа однородных независимых опытов с практической достоверностью можно утверждать, что частота события будет сколь угодно мало отличаться от его вероятности в отдельном опыте.

Классическое определение вероятности применимо только для очень узкого класса задач, где все возможные исходы опыта можно свести к схеме случаев. В большинстве реальных задач эта схема неприменима. В таких ситуациях требуется определять вероятность собы-тия иным образом. Для этого введем вначале понятие относительной частоты W(A) события A как отношения числа опытов, в которых наблюдалось событие А, к общему количеству проведенных испытаний:

(1.2)

где N – общее число опытов, М – число появлений события А.

Большое количество экспериментов показало, что если опыты проводятся в одинаковых условиях, то для большого количества испытаний относительная частота изменяется мало, колеблясь около некоторого постоянного числа. Это число можно считать вероятностью рассматриваемого события.

Определение 1.9. Статистической вероятностью события считают его относительную частоту или число, близкое к ней.

92. Вероятность противоположного события. Условная вероятность.

.

. Два единственно возможных события, обра­зующих полную группу, называются противоположными.

Если событие обозначено через А, то противоположное ему событие обозначается через . Из теоремы 17.2 следует, что

Например, если при стрельбе по мишени попадание — это событие А, то событие — это промах; сумма их вероятностей равна единице — при выстреле обязательно будет либо попа­дание, либо промах. То же самое и при подбрасывании монеты: обязательно выпадет либо орел, либо решка.

Пример 3. В магазине имеется 10 телевизоров, из которых 2 неисправных. Найти вероятность того, что среди наугад взя­тых 3-х телевизоров будет хотя бы один неисправный.

Решение. События "среди взятых телевизоров нет ни од­ного неисправного" и "есть хотя бы один неисправный" — про­тивоположные. Первое из них обозначим через А, а второе — через . Общее число способов, которыми можно взять 3 изде­лия из десяти, равно C . Число исправных телевизоров равно 8, число способов выборки из них трех изделий равно C , так что вероятность Р(А) = C