Пост-ка и мат.модель задачи ЦП.

ЦП-раздел мат.програм-ния ,изуч экстрем. задачи,в кот. на искомые перем налагается усл целочисл,а ОДР-конечна. Задача «о контейнерных перевозках»(о рюкзаке)Для перевозки n видов пр-ции исп-ся контейнер с m отсеками.Пр-ция хар-ся св-вом недел,т.е. ее можно взять 0,1,2,3,4…

С_j, j=1,n – полезность ед-цы j-й прод-ции

b_i,i=1,n – вместимость i-го отсека

а_ij, i=1,m, j=1,n – расходi-го отсека для перевозки ед прод-ции j-го вида

Треб-ся найти кол-во каждого вида прод-ции,погруж-ной в контейнер,кот-я обеспеч-ет max общую полезность рейса.

max(min)F= 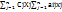{≤, =, ≥} bi, i=1,mxj≥0, и целые, j=1,n

Если для перевозки исп-ся один отсек и каждый вид прод-ии может быть взят или нет, то тогда задача будет иметь вид maxF= 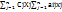≤ bi, Xj Є {0,1}, j=1,n

Реш зад ЦП мет отсеч

Будем рассматривать следующую задачу ЦП

Max(min) F=∑ⁿ_j=1c_ijx_ij(1)

∑ⁿ_j=1c_ijx_ij =b_i ,i=1,m (2)

x_j≥0, j=1,n (3)

x_j-целый, j=1,n (4)

Осн в алгоритме- построение доп.огран,кот.наз-ся правильн отсеч.ПО должно удовл.усл:

1)быть линейным

2)отсекать найденное оптим-оенецелочисл-ое решение задачи 1-3:

Алгоритм метода:

1.Реш задача (1)-(3),с отброшенным усл-м целочис-ти(4).

2.Если усл.целочисленности вып-ся по всем переменным,то оптимальн.решение з-чи(1)-(4) совпад-т с оптимальн.решением з-чи(1)-(3).Если же это усл.не выпол-ся хотя бы поодной перемен-й ,то переходим к шагу 3.Если з-ча(1)-(3)не разрешима,то и исходная з-ча не имеет реш-я.

3.Строится доп-ое ограничение,кот.отсекает часть ОДР,в кот.содерж-ся оптим-е решение з-чи (1)-(3) и не содер-ся ни одного допуст-го реш-я задачи(1)-(4)

4.Возвращ-ся к з-че с отброш-м условием целочисл-ти,но с расшир-й сис-мой осн-х ограничений.Добавляются огранич-я,построен-е на 3-ем шаге и вновь примен-ся симплексная процедура и т.д.

36. Метод Гомори (метод отсеч-я)Будем рассм следующую задачу ЦП

Max(min) F=∑ⁿ_j=1c_ijx_ij(1)

∑ⁿ_j=1c_ijx_ij =b_i ,i=1,m (2)

x_j≥0, j=1,n (3)

x_j-целый, j=1,n (4)

Алгоритм метода:

1.Решается задача (1)-(3),с отброшенным усл-м целочис-ти(4).

2.Если усл.целочисленности вып-ся по всем переменным,то оптимальн.решение з-чи(1)-(4) совпад-т с оптимальн.решением з-чи(1)-(3).Если же это усл.не выпол-ся хотя бы поодной перемен-й ,то переходим к шагу 3.Если з-ча(1)-(3)не разрешима,то и исходная з-ча не имеет реш-я.

3.Строится доп-ое ограничение,кот.отсекает часть ОДР,в кот.содерж-ся оптим-е решение з-чи (1)-(3) и не содер-ся ни одного допуст-го реш-я задачи(1)-(4)

4.Возвращ-ся к з-че с отброш-м условием целочисл-ти,но с расшир-й сис-мой осн-х ограничений.Добавляются огранич-я,построен-е на 3-ем шаге и вновь примен-ся симплексная процедура и т.д. Отличие выбора разрешающего элемента: Сначала рассм-ся строка,в кот содерж-ся отриц-е число в столбце свободн.членов и рассмат-ем все неотриц-е числа в этой строке. Выбираем люб.отрицат. число, кот и будет определять разрешающ. столбец. Для чисел с один-ми знаками в столбце свободн. членов и разреш столбце наход-ся симплекс-е отношения. Наименьш.симплексн.отнош и опред разреш-щую строку

37.

1.Явл-ся линейным

2.Отсекает найденное оптимальное нецелочисл-е знач-е з-чи (1)-(3)

3.Не отсекает ни одного из целочис-х реш-ий з-чи (1)-(4).

Рассмотрим i₀ –равенство(1):

x_i0= b_i0-∑x_j?спλ_i0jx_j(2)

a=[a]_{цел.часть}+{a}_{дроб.ч-ть},где 0<{a}< 1

3,7=3+0,7

-4,1=-5 +0,9

Представим b_i0 и λ_i0jв виде суммы дробной и целой части:b_i0=[ b_i0]+{ b_i0}; λ_i0j=[ λ_i0j]+{ λ_i0j}(3)

Подставим (3) в (2), получим:x_i0= ([b_i0]-∑_xj?сп[λ_i0j]xj)+ ([b_i0}-∑_xj?сп{λ_i0j}xj) (4)

Понятно,что 1-ая скобка-в сегда целое число.Для того,чтобы x_i0-было целым числом надо,чтобы величина L_i0={ b_i0}-∑_xj?сп{λ_i0j} xj _,тоже была целым числом.Покажем,что L_i0≤0.Предположим,что L_i0>0.По усл величина ∑_xj?сп{λi0j} xj не может быть отрицат.Т.к.дробные части 0<{λ_i0j}<1.По предложению следует,что дробная часть {b_i0}>1,а это противоречит определению дроб-ой части числа.След-но L_i0≤0Таким образом дополнит-ое огранич,кот.строит в пункте 3 алгоритма должно иметь вид: ([b_i0]-∑_xj?сп{λ_i0j}xj≤0 (5).

38.Теорема. Рассмотрим i₀ –равенство(1):

x_i0= b_i0-∑_xj?спλ_i0jx_j(2);

b_i0=[b_i0]+{ b_i0}

λ_i0j=[ λ_i0j]+{ λ_i0j} (3);

x_i0= ([b_i0]-∑_xj?сп[λ_i0j]xj)+ ([b_i0]-∑_xj?сп{λ_i0j}xj) (4);

([b_i0]-∑_xj?сп{λ_i0j}xj≤0 (5);

Суть теоремы: Нер-во (5)опред-т правильное отсечение Гомори,т.е.:

Max(min) F=∑ⁿ_j=1c_ijx_ij(1)

∑ⁿ_j=1c_ijx_ij =b_i ,i=1,m (2)

x_j≥0, j=1,n (3)

x_j-целый, j=1,n (4)

Метод ветвей и границ.

Для определённости будем рассчит з-чу нахожд макс ф-ции. Суть м-да заключ-ся в том,что сначала реш-ся з-ча без учёта целочис-сти.Если в полученном решении нек.переменные имеют дробные знач,то выбираем любую из дроб-х переменных и по ней строим 2-а ограничения.В первом ограничении величина переменной меньше или равна наименьшему целому числу,а во второй переменной ≥ целому числу +1.Таким образом исходная задача ветвится на 2 з-чи.Решаем каждую из подзадач и находим оптимальное решение.Если получ-е решения опять являются нецелыми,то дальнейшему ветвлению подлежит та ветвь,у которой значение ЦФ будет больше.Процесс решения сопровождается построением деревоветвл-ем.

Понят о ДП.Особен.

ДП(динамическое планирование)-метод нахожд-я реш-я в з-чах с многошаговой стр-рой.Суть метода ДП - идея постепенной, пошаговой оптимизации. Если трудно решить слож-ю задачу,то её след-т разбить на ряд более простых.Каждая новая задача оптим-ся не отдельно от осталь-х,а упр-ние на каждом шаге выбир-ся с учетом всех его последствий.Исключ-е-послед-й шаг,кот. мож. план-ся без учета посдед-вий.Особ-сть ДП:всю ДП целесообр-но разворач-ть от конца к началу