Прав «миним эл-та» (наим стоим»)
Просматр тарифы в распред-ной табл и в перв очередь заполн-ся клетка с миним знач тарифа. При этом в клетку запис-ся макс возмож знач поставки. Затем из рассмотрения исключ строку, соотв пост-ку, запасы которого полностью израсходованы, или столбец, соответствующий потребителю, спрос кот полн удовл. После этого из остав-ся клеток табл снова выбирают клетку с наим тарифом. Процесс распред закан-ся, когда все запасы пост-ков исчерп, а спрос потреб-ей полн удовл. В рез-те получ опорн план, кот должен содерж m=n-1клеток.
Теор о потенц. Алг теор
План ТЗ Х* явл. Оптим-м, если ему соотв-т система из m+n чисел Ui и Vj, кот.удовл-т след. Усл-м: 1) Ui+Vj=Cij, X*ij≠0; 2) ∆ij=cij-(Ui+Vj)≥0, X*ij=0 Док-во: ТЗ можно рассматр-ть как двойств. задачу к некот. исх. задачи,реш-ой на max. Каждому i-му огранич-ю ТЗ в исх. задаче соотв-т перемен. Ui,i=1,m, а j-му огранич-ю x1j+x2j+…+xmj=bj перем. Vj, j=1,n. Тогда задача имеет вид: maxφ= 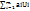 +
+ 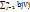 , Ui+Vj≤Ciji=1,m, j=1,n Обозн. ч/з X*,Y*(Ui,Vj)-ОП двойств. исх. з-чи. На основ-ии 1-й теор. двойственности равенство: minF=maxφ. А на основании 2-й теор. двойств. выполн. усл.: 1)Ui+Vj=Cij, xij>0; 2)Ui+Vj≤Cij, xij=0, i=1,mj=1,n Из теор. след., что для ОП ТЗ необх. выполн-е усл-й: 1)кажд. занятой кл-ке в распред. табл. соотв. ∑ потенциалов, ровная тарифу этой клетки; 2)кажд. своб. кл-ке соотв-т ∑ потенц-в, не превыш-я тарифа этой кл-ке. Эк-ки оценка показ-т на сколько ден.ед. уменьш. трансп. издержки от загрузки данной кл-ки ед. груза. Алгоритм реш. ТЗ мет. потенциалов.1)Усл.ТЗ записать в форме распред-й табл., но снач. провер. закр. или откр. модель ТЗ. 2) по 1-му из правил строим ОП. 3)Опред-м пот-лы поставщ-в и потреб-й, для этого реш-ся сист. ур-ний Ui+Vj=Cij для занятых кл-к. 4) Опред-ем оценки своб. кл-к ∆ij>0, то получим ОП единствен-й, если хотя бы 1 из оценок ∆ij=0, то имеем бесчислен.мн-во оптим. пл-в.
, Ui+Vj≤Ciji=1,m, j=1,n Обозн. ч/з X*,Y*(Ui,Vj)-ОП двойств. исх. з-чи. На основ-ии 1-й теор. двойственности равенство: minF=maxφ. А на основании 2-й теор. двойств. выполн. усл.: 1)Ui+Vj=Cij, xij>0; 2)Ui+Vj≤Cij, xij=0, i=1,mj=1,n Из теор. след., что для ОП ТЗ необх. выполн-е усл-й: 1)кажд. занятой кл-ке в распред. табл. соотв. ∑ потенциалов, ровная тарифу этой клетки; 2)кажд. своб. кл-ке соотв-т ∑ потенц-в, не превыш-я тарифа этой кл-ке. Эк-ки оценка показ-т на сколько ден.ед. уменьш. трансп. издержки от загрузки данной кл-ки ед. груза. Алгоритм реш. ТЗ мет. потенциалов.1)Усл.ТЗ записать в форме распред-й табл., но снач. провер. закр. или откр. модель ТЗ. 2) по 1-му из правил строим ОП. 3)Опред-м пот-лы поставщ-в и потреб-й, для этого реш-ся сист. ур-ний Ui+Vj=Cij для занятых кл-к. 4) Опред-ем оценки своб. кл-к ∆ij>0, то получим ОП единствен-й, если хотя бы 1 из оценок ∆ij=0, то имеем бесчислен.мн-во оптим. пл-в.
Циклы и их использ
Для перехода от одного ОП к другому использ-я циклы. Циклпредст. замкн-ю ломаную линию, сост-ю из звеньем, кот пересек-ся под прямым углом. Цикл.включ. 1 своб. кл-ку. В цикле всегда четное число кл-к. Цикл строится для свободн. кл-ки. Если ломанная линия пересек-ся, то точки самопересечения не явл. вершинами. Для наиб перспективн. кл-ки строится замкнутый цикл с вершинами в загружен.кл-х. Вершинами этого цикла усл. приписыв. знаки: своб. кл-ке «+», следующ. «-» и т.д. из поставок в кл-х цикла с «отриц.» верш. выбир. наименьш. кол-во груза, кот перемещ-ся. по кл-м этого цикла: прибавл. в положит. верш. и вычет. в отрицат., в рез-те чего баланс цикла не наруш.
32.Услож постановки ТЗ1)Для мин-ции сумм.затрат на пр-во и перевозку прод-ии, критерий оптим-ти – сумма затрат на пр-во 1ед.груза и на перевозку.2)Если нужно вводить огранич-я, согл. кот-ым отд.поставки от определ.пост-ка опред.потреб-лю должны быть исключены, то в матрице перевозок,содерж-ей оптим.план, определ.клетки должны быть своб-ми(т.е искусств-но завыш.тариф в клетках, перевозки ч/з кот-ые след.запретить)3)нужно учит-ть огран-я по пропуск.спос-ти маршруток. Напр.,если по маршруту AkBsможно провести не >d ед.прод-ии, то столбец Bs разбив-ся на 2: Bs’ и Bs’’. В 1-м столбце спрос=разности м/у действит.спросом и огр-ем Bs-d, а во2-м ст-це спрос=d.Тарифы в 2-х ст-ах одинак-ы, а в клетке AkBs’тариф иск-но завыш-ся.4)Если некот.поставки по некот.маршр-м должны войти в оптим.план, даже если это невыгодно, то тариф иск-но заниж-ся.
ТЗ с макс-ей ЦФ
1.Нач.опор.план строится методом max тарифа
2.план перевозок – оптим-ый, кот-ым соотв-ет своб.клетки с оценками <=0
3.выбор перспект-ой клетки, кот-ый подлежит заполн-ю, должен произв-ся по полож.оценке
