Формулы Бейеса вычисления вероятности.

Пусть Н₁, Н₂ , ... , Нn - попарно-несовместные события, вероятности которых Р(Н_i) ≠ О (i = 1,2, ... , n), и событие А c Н₁ + Н₂ + .. + Hn, для которого известны условные вероятности Р(А/ Нi) (i = 1,2, .., n). Произведен опыт, в результате которого появилось событие А . Условные вероятности событий Н₁, Н₂,..., Нn относительно события А определяются формулами

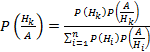(k=1,2,…, n) (1)

Или

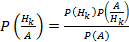(2)

Где

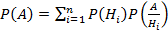– формула полной вероятности

Формула (1) называется формулами Бейеса

Вероятности P(Hk ) (k=1,2, .. . , n)событий Н1Н2 , ... , Нn до опьrra называются априорными вероятностями (от латинского apriory, что озна­

чает "сперва", т. е. в данном случае до того, как бьшпроизведенопыг). Вероятности Р(Н k /А) (k = 1,2, ... , n) тех же собьrrий называются апрoсmeриорными (от латинского слова аposteriori, что означает "после", Т.е. в данном случае после опыта).

Пример. На склад поступило 1000 подшипников. Из них 200 изготовлены на 1-м заводе, 460—на 2-м и 340 - на 3-м. Вероятность того, что подшипник окажется нестандартным, для 1-го завода равна 0,03, для 2-го — 0,02, для 3-го — 0,01. Взятый наудачу подшипник оказался нестандартным. Какова вероятность того, что он изготовлен 1-м заводом?

Решение: Пусть A — событие, состоящее в том, что взятый Подшипник нестандартный, а H1, H2, H3 - гипотезы, что он изготовлен соответственно 1-м, 2-м или 3-м заводом. Вероятности указанных гипотез составляют:

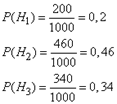
Из условия задачи следует, что

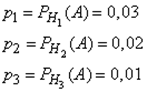
Найдем P_A(H₁), т. е. вероятность того, что подшипник, оказавшийся нестандартным, изготовлен 1-м заводом. По формуле Бейеса имеем

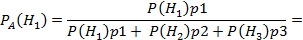
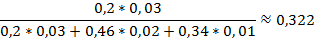
Многоугольник распределения СВХ – выпадение гербов при бросании трех монет.

Законом распределения дискретной случайной величины называется соответствие между значениями x₁, x₂, x₃, ... этой величины и их вероятностями p₁,p₂,p_З, ....

Закон распределения дискретной случайной величины может быть задан таблично или аналитически (т.е. с помощью формул).

Если дискретная случайная величина Х принимает конечное множество значений x₁, x₂, ... , х_n соответственно c вероятностями p₁, p₂, ... , p_n, то ее закон распределения определяется формулами:

P(X = x_k) = p_k (k =1,2,… n),

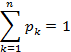
Этот закон можно задать и таблицей:

X	x1	x2	…	xn
P	p1	p2	…	pn

В этой таблице сумма вероятностей также равна единице: р₁ + р₂ + .. . + р_n = 1. События (Х = X_k ), k = 1, 2, ... , n, образуют полную

группу событий, поэтому выполняется равенство. Для наглядности закон распределения дискретной случайной величины изображают графически, для чего в прямоугольной декартовой системе координат строят точки (x_k, p_k) и соединяют их последовательно отрезками прямых. Получающаяся при этом ломаная линия называется многоугольником распределения случайной величины Х.

Дискретные и непрерывные случайные величины. Примеры.

Дискретной случайной величиной называется случайная величина, которая в результате испытания принимает отдельные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным. Примеры дискретной случайной величины: запись показаний спидометра или измеренной температуры в конкретные моменты времени.

Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени.

Любая случайная величина имеет свой закон распределения вероятностей и свою функцию распределения вероятностей. Прежде, чем дать определение функции распределения, рассмотрим переменные, которые её определяют. Пусть задано некоторое х – действительное число и получена случайная величина X, при этом (x>X). Требуется определить вероятность того, что случайная величина Х будет меньше этого фиксированного значения х.

Функцией распределения случайной величины Х называется функция F(х), определяющая вероятность того, что случайная величина Х в результате испытания примет значение меньшее значения х, то есть:

F (х) = Р(Х < х ).

(5.1)

где х – произвольное действительное число.

Случайная величина (непрерывная или дискретная) имеет численные характеристики:

Математическое ожидание М (Х). Эту характеристику можно сравнивать со средним арифметическим наблюдаемых значений случайной величины Х.

Дисперсия D(X). Это характеристика отклонения случайной величины Х от математического ожидания.

Среднее квадратическое отклонение s(Х) для дискретной и непрерывной случайной величины Х – это корень квадратный из ее дисперсии:

.

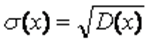(5.2)

Далее рассматриваются отличия между дискретной и непрерывной случайными величинами.

Формула Бернулли вычисления вероятности. Примеры

Опыты α₁, α₂,… называются независимыми, если любая комбинация их исходов является совокупностью независимых событий. В вероятностной схеме Бернулли рассматривается последовательность n независимых опытовα₁, α₂,… α_nв каждом из которых некоторое событие A может наступить с одной и той же вероятностью p= P(A). Условно это событие рассматривается как успех, а его ненаступление (событие ) – как неудача. Вероятность неудачи q = 1 - p в каждом опыте равна.

Пусть для заданного целого числа k (0 ≤ k ≤ n) Pn(k) обозначает вероятность того, что в n опытах успех наступит ровно k раз. Имеет место формула Бернулли:

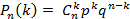
Вероятности P_n(k) (k = 0,1,…, n) называются биномиальными в силу того, что правая часть формулы представляет собой общий член разложения бинома Ньютона:

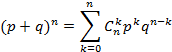
Так как p + q = 1, то из формулы бинома Ньютона следует, что сумма всех биномиальных вероятностей равна 1:

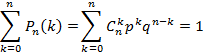
Пример 1. Вероятность попадания в мишень при одном выстреле для данного стрелка равна 0.8 и не зависит от номера выстрела. Требуется найти вероятность того, что при 5 выстрелах произойдет ровно 2 попадания в мишень

Решение. В этом примере n = 5, р = 0.8 и k = 2; по формуле Бернулли находим:

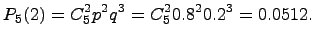
Пример 2. Вероятность попадания в мишень при одном выстреле для данного стрелка 0,7 и не зависит от номера выстрела. Найти вероят­

ность того, что при 5 выстрелах произойдет ровно 2 попадания в мишень.

Решение. Поскольку р = 0,7, то q = 1 - p = 1 - 0,7 = 0,3. По условию n = 5, k = 2, по формуле находим

P₅(2) = C₅²p²q^5-2 = 10 *(0,7)² * (0,3)³ = 0,1323

Формула Пуассона вычисления вероятности. Примеры

В одинаковых условиях производится n независимых испытаний, в каждом из которых может появиться событие А с вероятностью р или событие 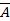с вероятностью q (q = 1 - р). Вероятность того, что при n испытаниях событие А появится k раз (ине появится n - k раз) определяется формулой Бернулли

Рассмотрим случай, когда n является достаточно большим, а р - достаточно малым; положим nр = а, где а - некоторое число.

Распределением Пуассона называется распределение вероятностей дискретной случайной величины, определяемое формулой:

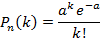
Постоянную a=np, входящую в формулу называют параметром распределения Пуассона.

Закон распределения Пуассона можно записать в виде следующей таблицы:

X				…	k	…
P	e-a	ae-a		…		…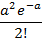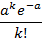

Пример 1. На предприятии изготовлено и отправлено заказчику 100000 бутылок пива. Вероятность того, что бутылка может оказаться битой, равна 0,0001. Найти вероятность того, что в отправленной партии будет ровно три и ровно пять битых бутылок.

Решение. Дано: n = 100000, p = 0,0001, m = 3 (m = 5).

a=np=10

Воспользуемся формулой Пуассона

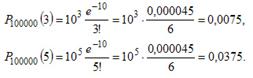
Пример 2. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течении времениТ равна 0,002. Найти вероятность того, что за времяТ откажут ровно три элемента.

Решение. По условию дано: n=10000, p = 0,002, a=np = 2, k =3

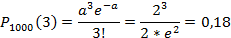
21.Математическое ожидание случайной величины.

МО -характеризует среднее взвешенное значение случайной величины.

Для вычисления математического ожидания для ДСВ каждое значение x_i учитывается с «весом», пропорциональным вероятности этого значения.

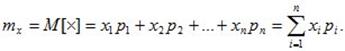(6.1)

M[X]-оператор математического ожидания;

m_x-- число, полученное после вычислений по формуле.

Для НСВ заменим отдельные значения 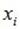непрерывно изменяющимся параметром 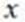, соответствующие вероятности 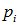- элементом вероятности 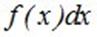, а конечную сумму – интегралом: 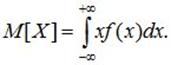(6.2)

Механическая интерпретация понятия математического ожидания: на оси абсцисс расположены точки с абсциссами 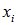, в которых сосредоточены соответственно массы р₁, р₂,...., причем 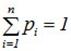. Тогда МО – абсцисса центра тяжести. Для НСВ – масса распределена непрерывно с плотностью .

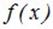Для смешанных случайных величин математическое ожидание состоит из двух слагаемых.

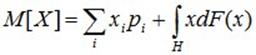, (6.3)

где сумма распространяется на все значения x_i, имеющие отличные от нуля вероятности, а интеграл – на все участки оси абсцисс, где функция распределения F(x) непрерывна.

Физический смысл математического ожидания – это среднее значение случайной величины, т.е. то значение, которое может быть использовано вместо конкретного значения, принимаемого случайной величиной в приблизительных расчетах или оценках.