Графическое представление выборки. Полигон и гистограмма.

Для наглядного представления о поведении исследуемой случайной величины в выборке можно строить различные графики. Один из них – полигон частот: ломаная, отрезки которой соединяют точки с координатами (x1, n1), (x2, n2),…, (xk, nk), где xi откладываются на оси абсцисс, а ni – на оси ординат. Если на оси ординат откладывать не абсолютные (ni), а относительные (wi) частоты, то получим полигон относительных частот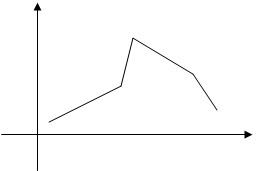

Для непрерывного признака графической иллюстрацией служит гистограмма, то есть ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высотами – отрезки длиной ni /h (гистограмма частот) или wi /h (гистограмма относительных частот). В первом случае площадь гистограммы равна объему выборки, во втором – единице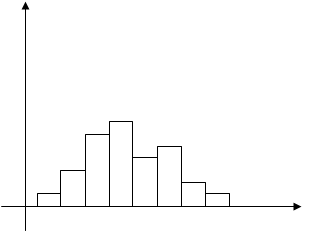

41) Статистические оценки параметров распределения , несмещенные, эффективные и состоятельные оценки.
Пусть x1, x2, …, xn – выборка объема n из генеральной совокупности с функцией распределения F(x ). Рассмотрим методы нахождения оценок параметров этого распределения. Рассмотрим для этого выборочное распределение, т.е. распределение дискретной случайной величины, принимающей значения x1, x2, …, xn с вероятностями, равными 1/n . Числовые характеристики этого выборочного распределения называются выборочными (эмпирическими) числовыми характеристиками. Следует отметить, что выборочные числовые характеристики являются характеристиками данной выборки, но не являются характеристиками распределения генеральной совокупности. Однако эти характеристики можно использовать для оценок параметров генеральной совокупности.
Точечной называют статистическую оценку, которая определяется одним числом.
Несмещенной называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки.
Состоятельной называется статистическая оценка, которая при п→∞ стремится по вероятности к оцениваемому параметру (если эта оценка несмещенная, то она будет состоятельной, если при п→∞ ее дисперсия стремится к 0)..
Эффективной называют точечную оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию.
В математической статистике показывается, что состоятельной, несмещенной оценкой генерального среднего значения а является выборочное среднее арифметическое:

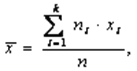
где хi – варианта выборки, ni – частота варианты хi, – объем выборки.

42)Генеральная и выборочная совокупность
Генеральная средняя. Пусть изучается генеральная совокупность относительно количественного признака Х. Генеральной средней называют среднее арифметическое значений признака генеральной совокупности. Если все значения признака различны, то

Если значения признака имеют частоты N1, N2, …, Nk, где N1 +N2+…+Nk= N, то

Выборочная средняя.