При этом сумма вероятностей, стоящих во всех клетках таблицы, равна 1.

Зная закон распределения двумерной случайной величины, можно найти законы распреде-ления ее составляющих. Действительно, событие Х = х1 представляется собой сумму несовместных событий (X = x1, Y = y1), (X = x1, Y = y2),…, (X = x1, Y = ym), поэтому

р(Х = х1) = p(x1, y1) + p(x1, y2) +…+ p(x1, ym) (в правой части находится сумма вероятностей, стоящих в столбце, соответствующем Х = х1). Так же можно найти вероятности остальных возможных значений Х. Для определения вероятностей возможных значений Y нужно сложить вероятности, стоящие в строке таблицы, соответствующей Y = yj.

31) Числовые характеристики двумерных случайных величин, функции регрессии.

Такие характеристики, как начальные и центральные моменты, можно ввести и для системы двух случайных величин.

Начальным моментом порядка k, s двумерной случайной величины (Х, Y) называется математическое ожидание произведения Xk на Ys:

αk,s = M (XkYs). (9.6)

Для дискретных случайных величин 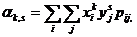для непрерывных случайных величин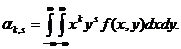

Центральным моментом порядка k, s двумерной случайной величины (Х, Y) называется математическое ожидание произведения (X – M(X))k на (Y – M(Y))s:

μk,s = M((X – M(X))k(Y – M(Y))s). (9.7)

Для дискретных случайных величин 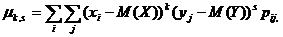для непрерывных случайных величин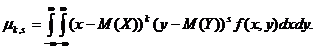

При этом М(Х) = α1,0, M(Y) = α0,1, D(X) = μ2,0, D(Y) = μ0,2.

32)Ковариация, коэффициент корреляции.
Ковариация представляет собой математическое ожидание произведения центрированных случайных величин X и Y и характеризует степень линейной статистической зависимости величин X и Y и рассеивание относительно точки (mx, my):

Kxy = 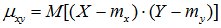, (11.9)

Или

(11.10)

Расчетные формулы для определения ковариации:

(11.11)

Для характеристики связи между случайными величинами Х и Y в чистом виде переходят к безразмерной характеристике, которая называетсяКоэффициент корреляции rxyхарактеризует степень линейной зависимости величин:

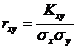
Свойства коэффициента корреляции:

1. Абсолютная величина коэффициента корреляции двух случайных величин не превышает единицы:

2. │rxy│=1 если Y=aХ+b

Доказательство: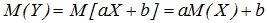

Подставим в выражение

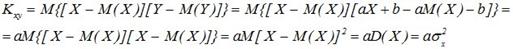
т.к.

Найдем дисперсию Y: , т.е.

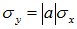, коэффициент корреляции: Þ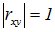

Коэффициент корреляции служит для оценки тесноты линейной связи между Х и Y: чем ближе абсолютная величина коэффициента корреляции к 1, тем связь сильнее, чем ближе к 0, тем слабее.
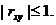Доказательство. Докажем сначала, что Действительно, если рассмотреть случай-ную величину и найти ее дисперсию, то получим: 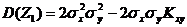. Так как дисперсия всегда неотрицательна, то 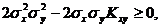откуда Отсюда 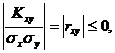что и требовалось доказать.

3. Если величины X и Y независимы, то rxy = 0.

33. Двумерный нормальный закон распределения

Систему случайных величин можно интерпретировать как случайную точку на плоскости. Нормальный закон распределения для системы (Х,У) называется двумерным нормальным законом распределения и имеет плотность вероятности