Эллипс и его каноническое уравнение
Линии второго порядка
Общее уравнение линии второго порядка имеет следующий вид:
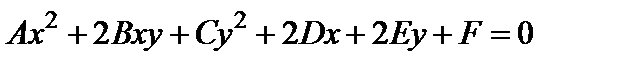 , (1)
, (1)
где A, B, C, D, E, F – любые заданные числа, но A, B и C одновременно не равны нулю 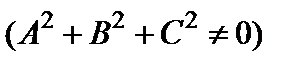 .
.
Теорема 1.Пусть в прямоугольной системе координат Оху заданообщее уравнение линии второго порядка (1). Тогда существует такаяпрямоугольная система координат, в которой уравнение (1) принимает один из следующих девяти простейших (канонических) видов:
1) эллипс 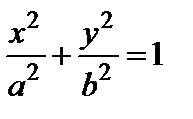 ;
;
2) мнимыйэллипс 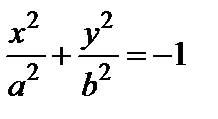 ;
;
3) пара мнимых пересекающихся прямых 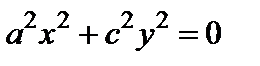 ;
;
4) гипербола 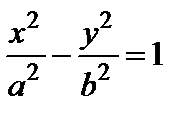 ;
;
5) пара пересекающихся прямых 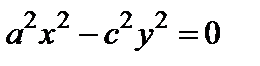 ;
;
6) парабола 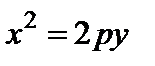 ;
;
7) пара параллельных прямых 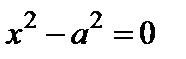 ;
;
8) пара мнимых параллельных прямых 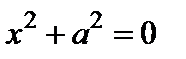 ;
;
9) пара совпадающих прямых 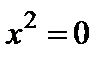 .
.
В этих формах х и у равноправны, т.е. их можно менять местами.
Гипербола
Гиперболой называется множество точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек 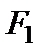 и
и 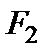 , называемых фокусами, есть величина постоянная, равная
, называемых фокусами, есть величина постоянная, равная 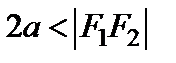 .
.
Пусть 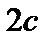 – расстояние между фокусами
– расстояние между фокусами 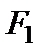 и
и 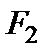 . Выберем декартову систему координат
. Выберем декартову систему координат 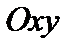 так, чтобы
так, чтобы 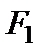 и
и 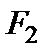 находились на оси
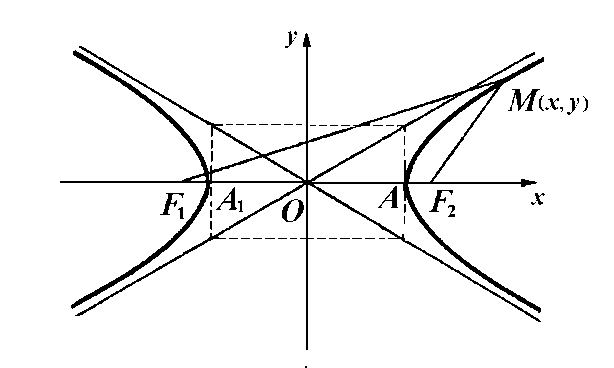
находились на оси 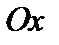 симметрично относительно начала координат (рис. 2).
симметрично относительно начала координат (рис. 2).
Если 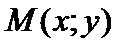 – произвольная точка гиперболы, то, по определению,
– произвольная точка гиперболы, то, по определению,
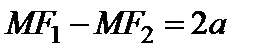 или
или 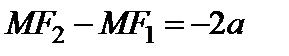 .
.
| Рис. 2 |
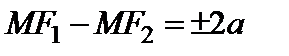 .
.
Отметим, что  , так как из треугольника
, так как из треугольника 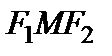 имеем
имеем 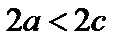 .
.
Рассуждая аналогично, как и при выводе канонического уравнения эллипса, получим каноническое уравнение гиперболы
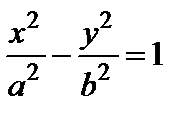 , где
, где 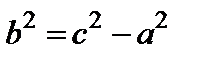 .(
.(
6.Парабола
Параболой называется множество точек плоскости, равноудаленных от данной точки F, называемой фокусом, и от данной прямой L, называемой директрисой.
Для вывода канонического уравнения параболы выберем декартову систему координат Оху так, чтобы ось Ох проходила через фокус F перпендикулярно директрисе, а начало координат О поместим на одинаковых расстояниях от фокуса и директрисы (рис.3).
2 LnhtbFBLAQItAAoAAAAAAAAAIQDpuymjmFYAAJhWAAAUAAAAAAAAAAAAAAAAANsIAABkcnMvbWVk aWEvaW1hZ2UxLnBuZ1BLBQYAAAAABgAGAHwBAAClXwAAAAA= "> 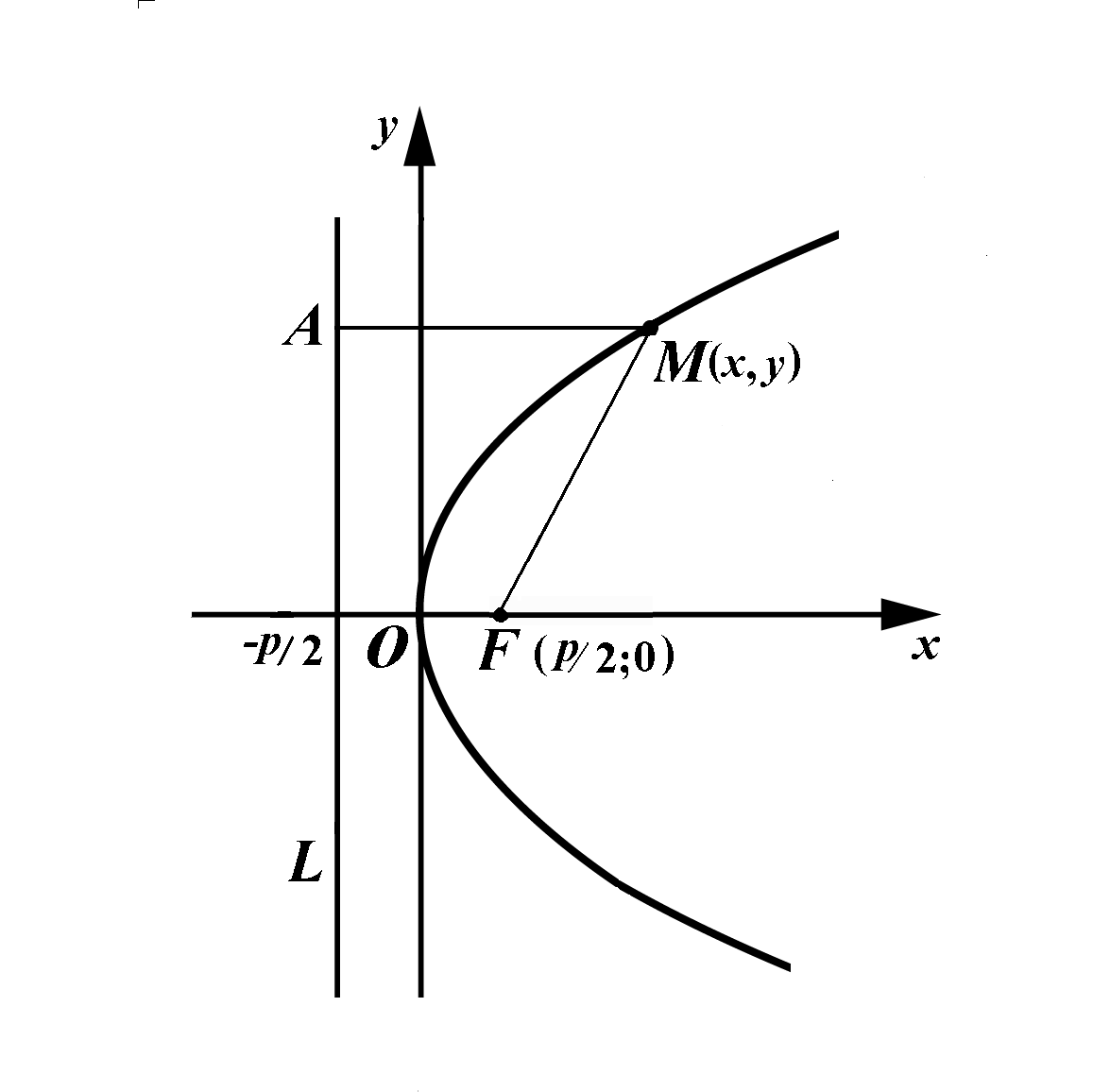
| Рис. 3 |
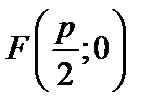 , а уравнением директрисы является
, а уравнением директрисы является 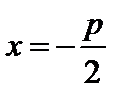 .
. Пусть М(х;у) – произвольная точка параболы. Тогда, согласно ее определению, имеем
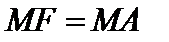 . (18)
. (18)
Точка А имеет координаты 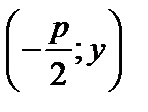 . Имеем
. Имеем
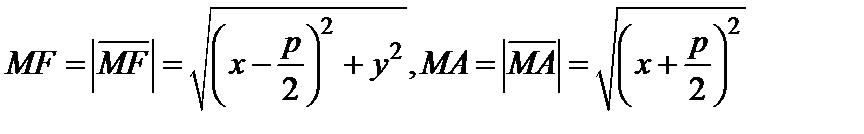 . (19)
. (19)
Из (18) и (19) получаем
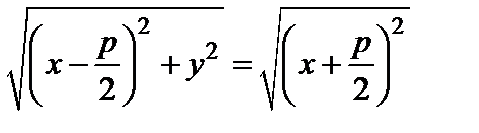 . (20)
. (20)
Отсюда 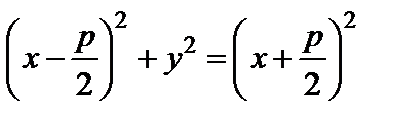 или
или 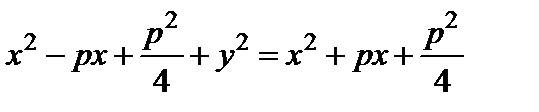 . Окончательно получаем
. Окончательно получаем
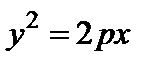 . (21)
. (21)
Уравнение (21) называется каноническим уравнением параболы, изображенной на рис. 3
Действия над матрицами.
Суммой двух матриц 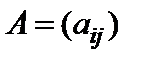 и
и 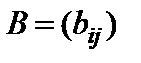 одинаковых размеров
одинаковых размеров 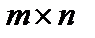 называется матрица
называется матрица 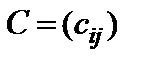 тех же размеров, каждый элемент которой равен сумме соответствующих элементов матриц A и B:
тех же размеров, каждый элемент которой равен сумме соответствующих элементов матриц A и B:
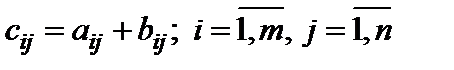 . (2)
. (2)
Для обозначения суммы матриц A и B используют запись A+B. Операция нахождения суммы данных матриц называется сложением матриц.
Например,
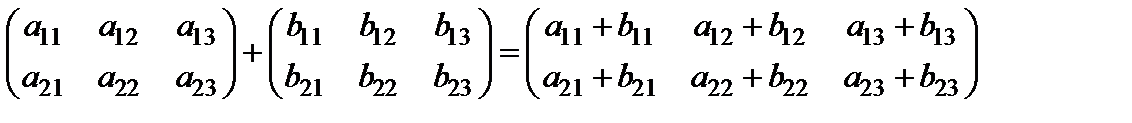 .
.
Таким образом, можно складывать матрицы только одинаковых размеров.
Из определения сложения матриц и соответствующих свойств сложения действительных чисел вытекает, что эта операция обладает переместительным и сочетательным свойствами:
1) 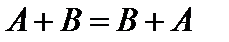 ,
,
2) 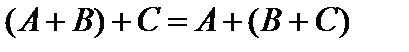 ,
,
где A,B,C – произвольные матрицы одинаковых размеров.
Очевидно, что операцию сложения матриц можно распространить на случай любого числа слагаемых.
Произведением матрицы 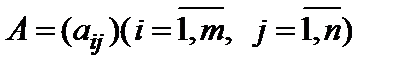 на число
на число 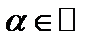 называется матрица
называется матрица 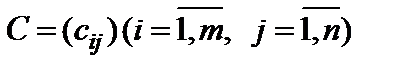 , каждый элемент которой есть произведение соответствующего элемента матрицы A и числа
, каждый элемент которой есть произведение соответствующего элемента матрицы A и числа 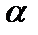 :
: 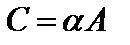 , т.е.
, т.е.
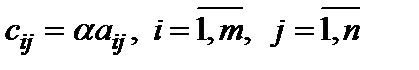 . (3)
. (3)
Операция нахождения произведения матрицы на число называетсяумножением матрицы на число.
Например,
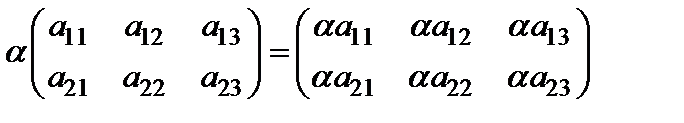 .
.
Из определения (3) произведения матрицы на число вытекают следующие свойства:
1) 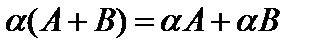 ,
,
2) 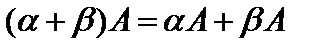 ,
,
3) 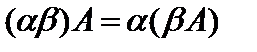 .
.
Здесь 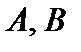 – матрицы одинаковых размеров, а
– матрицы одинаковых размеров, а 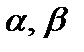 – числа из
– числа из  .
.
Разностью 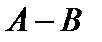 двух матриц
двух матриц 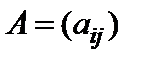 и
и 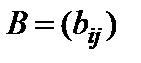 одинакового размера
одинакового размера 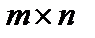 назовем матрицу
назовем матрицу 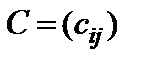 такого же размера, которая получается с помощью правила
такого же размера, которая получается с помощью правила
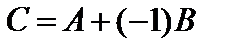 . (4)
. (4)
Из равенств (4), (3), (2) следует, что каждый элемент 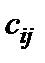 матрицы
матрицы 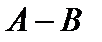 есть разность соответствующих элементов матриц A и B, т.е.
есть разность соответствующих элементов матриц A и B, т.е. 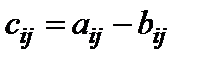 ,
, 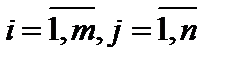 .
.
Произведением двух матриц
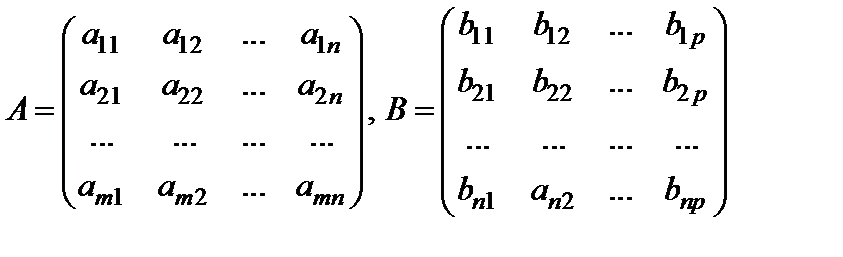
называется матрица
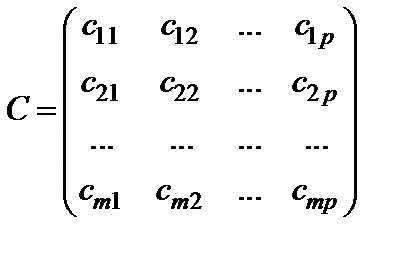 ,
,
у которой каждый элемент 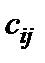 , стоящий на пересечении i-той строки
, стоящий на пересечении i-той строки
и j-го столбца, равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B:
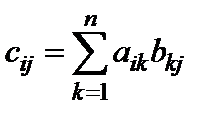 ,
, 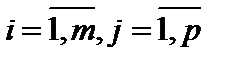 . (5)
. (5)
Таким образом, 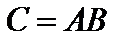 . Операция нахождения произведения данных матриц называется умножением матриц.
. Операция нахождения произведения данных матриц называется умножением матриц.
Например:
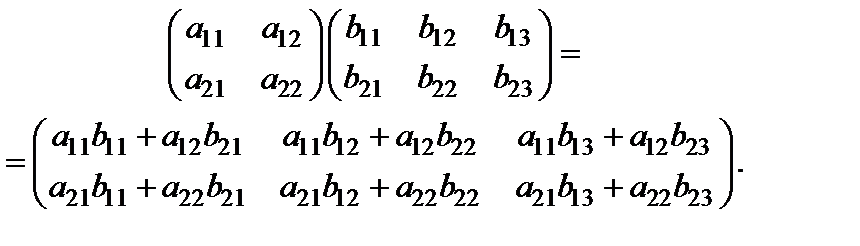
Отметим, что операция умножения двух матриц выполнима тогдаи только тогда, когда число столбцов в первом сомножителе равно числу строк во втором.
Используя определение (5), без труда проверяется сочетательное свойство умножения матриц, а также распределительное свойство умножения относительно сложения:
1) 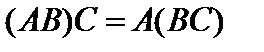 ,
,
2) 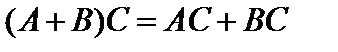 ,
,
3) 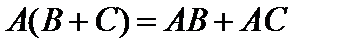 .
.
Операцию умножения матриц можно распространить на случай более двух сомножителей.
Заметим, что умножение AB всегда выполнимо, если сомножители A и B квадратные матрицы одного и того же порядка. Обратим внимание, что умножение матриц не обладает переместительным (коммутативным) свойством. Действительно, например, для матриц
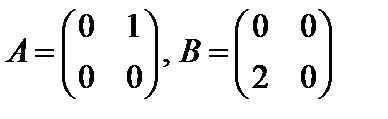
имеем
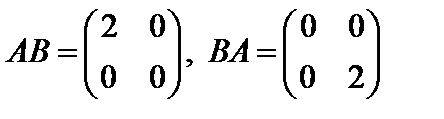 .
.
Если 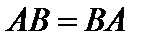 , то матрицы
, то матрицы 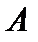 и
и 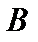 называются перестановочными или коммутирующими между собой.
называются перестановочными или коммутирующими между собой.
Отметим также, что диагональная матрица 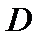 , у которой все диагональные элементы – равные числа, т.е.
, у которой все диагональные элементы – равные числа, т.е. 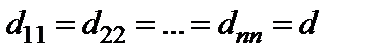 , коммутирует с любой квадратной матрицей
, коммутирует с любой квадратной матрицей 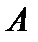 , в частности
, в частности
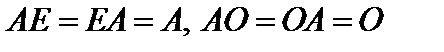 . (6)
. (6)
Из формулы (6) вытекает, что при умножении матриц единичная матрица 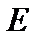 и нулевая
и нулевая 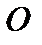 выполняют ту же роль, что числа 1 и 0 при умножении действительных чисел.
выполняют ту же роль, что числа 1 и 0 при умножении действительных чисел.
Заметим, что в отличие от чисел, произведение двух ненулевых матриц может дать нулевую матрицу.
Например, в случае
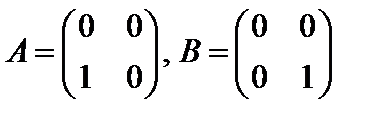
получаем
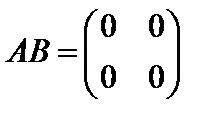 .
.
Введем еще одну важную операцию над матрицей – транспонирование матрицы. Пусть задана матрица A размеров 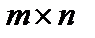 вида (1). После замены строк одноименными столбцами получим матрицу
вида (1). После замены строк одноименными столбцами получим матрицу 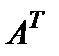 размеров
размеров 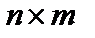 , которая называется транспонированной к заданной:
, которая называется транспонированной к заданной:
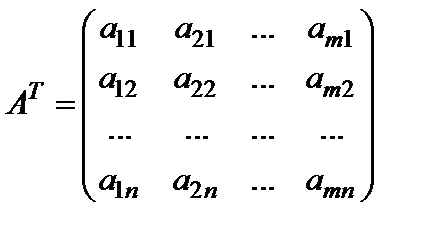 .
.
Число строк транспонированной матрицы равно числу столбцов матрицы  , а число столбцов – числу строк матрицы
, а число столбцов – числу строк матрицы  .
.
Операция нахождения матрицы 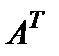 называется транспонированием матрицы, и для нее имеют место следующие свойства:
называется транспонированием матрицы, и для нее имеют место следующие свойства:
1) 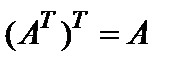 ,
,
2) 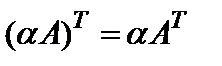 ,
,
3) 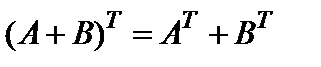 ,
,
4) 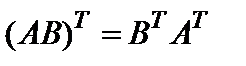 .
.
Если квадратная матрица 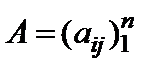 совпадает со своей транспонированной, т.е.
совпадает со своей транспонированной, т.е. 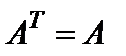 , то такая матрица называется симметрической.
, то такая матрица называется симметрической.
Матрицу 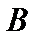 , для которой
, для которой 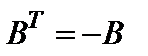 , называют кососимметрической.Легко видеть, что в кососимметрической матрице все элементы главной диагонали нули.
, называют кососимметрической.Легко видеть, что в кососимметрической матрице все элементы главной диагонали нули.
Например,
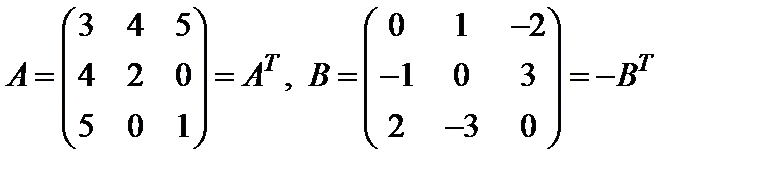 .
.
II Замечательный предел

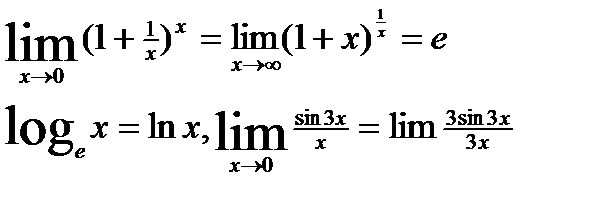
40-41.Непрерывные ф-ции.точки разрыва ,их классификация.Пусть дана ф-ция f(x),в кот.опред.точки промежутка – I и Xо. Ф-ция наз. непрерывной,если её предел равен знач.ф-ции в этой точке,т.е.

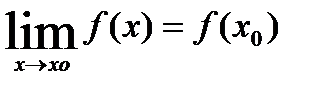

Пусть f(x) опред. в некот. окрестности т.Xo. Точку Xo наз.точкой разрыва ф-ции f(x).
Классификация точек разрыва:
Если Xo точка разрыва ф-ции и сущ. конечные пределы,то т.Xo явл. точкой
Разрыва первого рода.
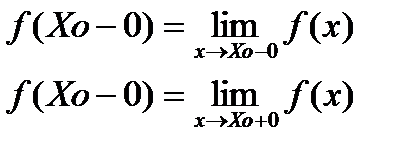
Величина f (Xo+0) - f (Xo-0) называется
скочком ф-ции в т.Xo. Если скачок равен 0 в т. разрыва.то Xo наз.точкой устронимого разрыва.Точка не явл. точкой I рода.наз. точкой II рода.Здесь под пределом понимается конечный предел: 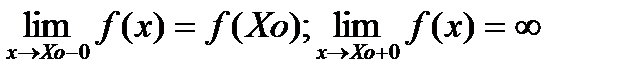 Свойства непрерывных функций:
Свойства непрерывных функций:
1)если f(x)непрер. на отр.(a;b)то она ограничена на отрезке и прин. найб. и наймен. значение.2)если f(x) опред. и непрерывна на отрезке,то хотя бы одна т. С леж. м/у точ. А и В такая,что f(c)=0.3)Если f(x) непрер. и прин. найб. и найм знач.,то для люб. С найдётся точка С  такая чтоf(c)=C
такая чтоf(c)=C
Линии второго порядка
Общее уравнение линии второго порядка имеет следующий вид:
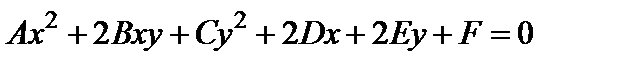 , (1)
, (1)
где A, B, C, D, E, F – любые заданные числа, но A, B и C одновременно не равны нулю 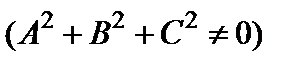 .
.
Теорема 1.Пусть в прямоугольной системе координат Оху заданообщее уравнение линии второго порядка (1). Тогда существует такаяпрямоугольная система координат, в которой уравнение (1) принимает один из следующих девяти простейших (канонических) видов:
1) эллипс 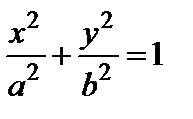 ;
;
2) мнимыйэллипс 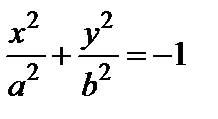 ;
;
3) пара мнимых пересекающихся прямых 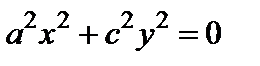 ;
;
4) гипербола 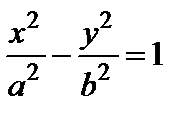 ;
;
5) пара пересекающихся прямых 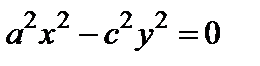 ;
;
6) парабола 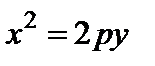 ;
;
7) пара параллельных прямых 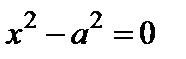 ;
;
8) пара мнимых параллельных прямых 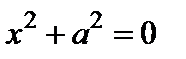 ;
;
9) пара совпадающих прямых 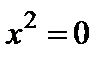 .
.
В этих формах х и у равноправны, т.е. их можно менять местами.
Эллипс и его каноническое уравнение
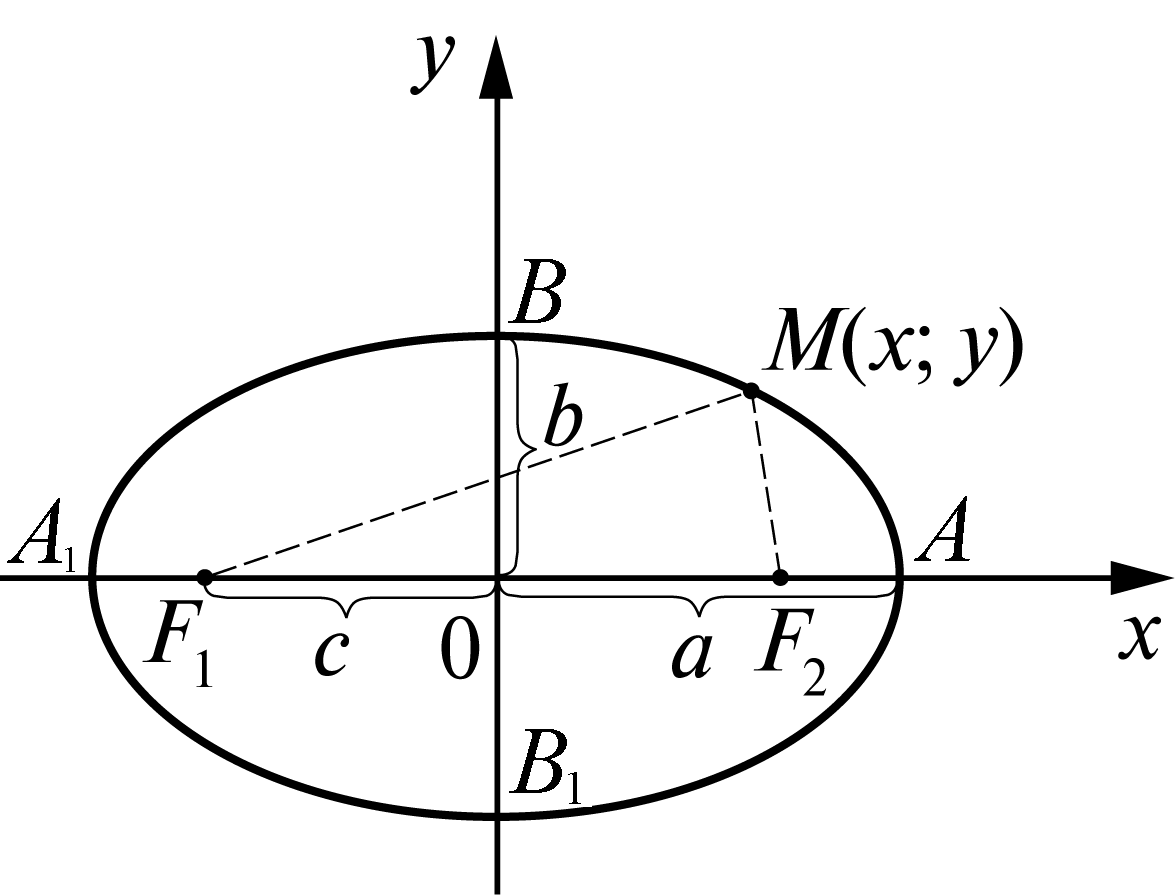
| Рис. 1 |
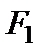 и
и 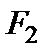 , называемых фокусами, есть величина постоянная, равная
, называемых фокусами, есть величина постоянная, равная 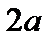 .
. Выведем уравнение эллипса. Для этого выберем декартову систему координат 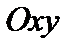 так, чтобы ось
так, чтобы ось 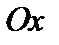 проходила через фокусы
проходила через фокусы 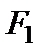 и
и 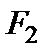 , расстояние между которыми обозначим
, расстояние между которыми обозначим 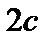 , а начало координат О находилось в середине отрезка
, а начало координат О находилось в середине отрезка 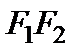 (рис. 1).
(рис. 1).
Тогда фокусы будут иметь координаты: 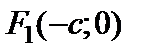 и
и 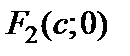 (рис. 1). Если
(рис. 1). Если 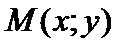 – произвольная точка эллипса, то согласно его определению, имеем:
– произвольная точка эллипса, то согласно его определению, имеем:
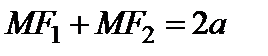 . (2)
. (2)
По формуле расстояния между двумя точками имеем
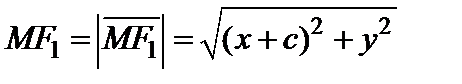 ,
, 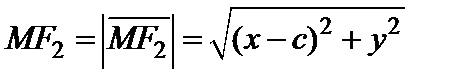 . (3)
. (3)
Подставляя (3) в (2), будем иметь
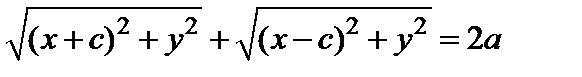 . (4)
. (4)
Уравнение (4) и есть уравнение эллипса. Приведем его к так называемому каноническому виду. Из (4) имеем
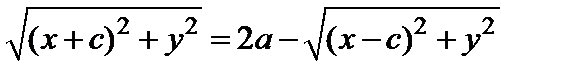 .
.
Возведя обе части последнего равенства в квадрат, получим
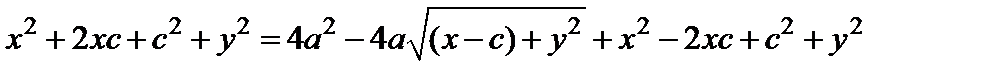 .
.
Отсюда
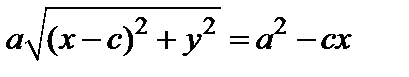 , (5)
, (5)
или, возведя обе части равенства (5) в квадрат, будем иметь
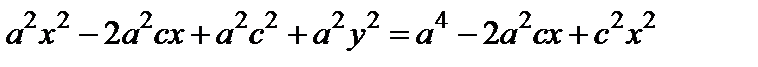 . (6)
. (6)
Из (6) получаем
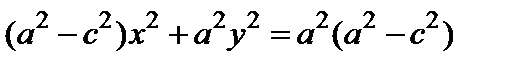 . (7)
. (7)
Так как  , то
, то 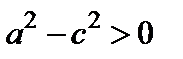 . Обозначим
. Обозначим 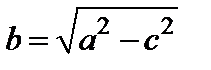 , тогда (7) примет вид
, тогда (7) примет вид
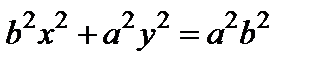 . (8)
. (8)
Разделив обе части (8) на 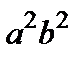 , получим уравнение эллипса вида:
, получим уравнение эллипса вида:
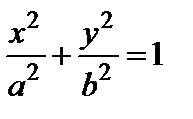 . (9)
. (9)
Показано, что любая точка эллипса удовлетворяет уравнению (9). Покажем теперь обратное: любая точка 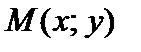 , удовлетворяющая уравнению (9), принадлежит эллипсу, т.е. удовлетворяет соотношению (2). Из уравнения (9) получаем
, удовлетворяющая уравнению (9), принадлежит эллипсу, т.е. удовлетворяет соотношению (2). Из уравнения (9) получаем
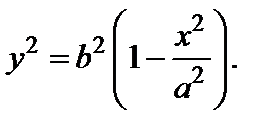
Используя это соотношение и учитывая, что 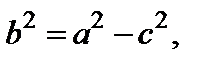 находим
находим
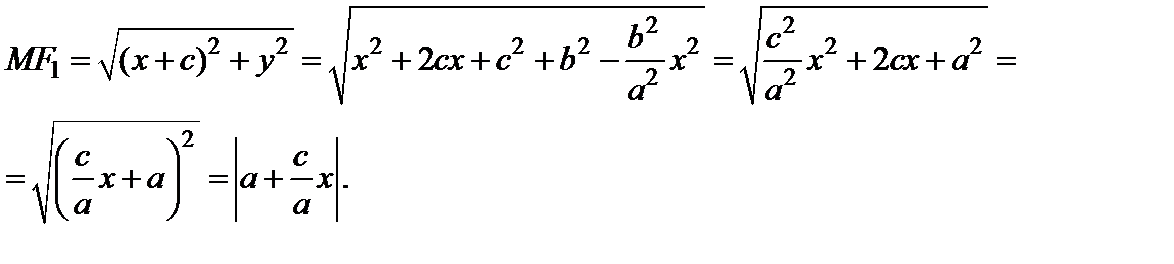
Так как, в силу равенства (9), 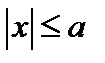 и, кроме того,
и, кроме того,  , то
, то 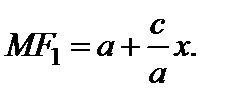
Аналогично можно получить формулу 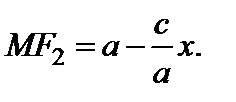 Складывая последние два равенства, получаем равенство (2).
Складывая последние два равенства, получаем равенство (2).
Итак, соотношение (9) является уравнением эллипса. Оно называется каноническим уравнением эллипса. Такой эллипс изображен на рис. 1. Эллипс симметричен относительно обеих осей координат. Из уравнения (9) при 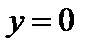 получаем:
получаем: 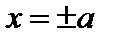 , т.е. эллипс пересекает ось
, т.е. эллипс пересекает ось 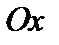 в двух точках:
в двух точках: 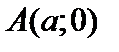 и
и 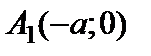 ; при
; при 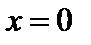 получаем:
получаем: 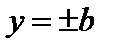 , т.е. эллипс пересекает ось
, т.е. эллипс пересекает ось 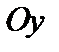 в двух точках:
в двух точках: 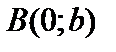 и
и 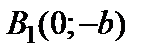 . Эти четыре точки называют вершинамиэллипса. Отрезок
. Эти четыре точки называют вершинамиэллипса. Отрезок 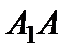 называется большой осью эллипса, а отрезок
называется большой осью эллипса, а отрезок 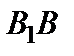 – его малой осью. Значит,
– его малой осью. Значит, 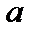 – длина большой полуоси эллипса,
– длина большой полуоси эллипса, 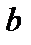 – длина малой полуоси эллипса.
– длина малой полуоси эллипса.
Уравнение (9) можно рассматривать и в случае 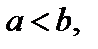 оно определяет эллипс с большой полуосью
оно определяет эллипс с большой полуосью 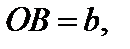 фокусы такого эллипса лежат на оси Oy.
фокусы такого эллипса лежат на оси Oy.
В том случае, когда 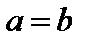 , уравнение (9) имеет вид
, уравнение (9) имеет вид 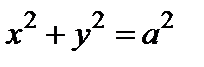 и определяет окружность радиуса а с центром в начале координат. В этом случае
и определяет окружность радиуса а с центром в начале координат. В этом случае 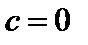 .
.
Эксцентриситетомэллипса называется отношение расстояния между фокусами к длине большой оси, т.е.
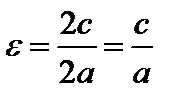 . (10)
. (10)
Поскольку  , то для любого эллипса
, то для любого эллипса 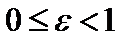 , причем случай
, причем случай 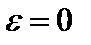 соответствует окружности.
соответствует окружности.
Геометрически 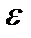 характеризует степень сжатия эллипса.
характеризует степень сжатия эллипса.
Действительно, из (10) и равенства 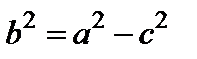 вытекает, что
вытекает, что 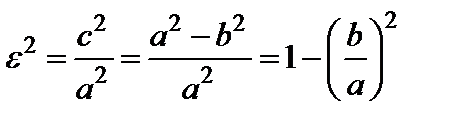 .
.
Значит,
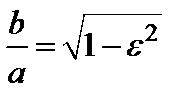 . (11)
. (11)
Из (11) видно, что чем больше 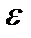 , тем меньше отношение
, тем меньше отношение 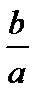 и тем больше вытянут эллипс. Две прямые, перпендикулярные большой оси эллипса и расположенные симметрично относительно центра на расстоянии
и тем больше вытянут эллипс. Две прямые, перпендикулярные большой оси эллипса и расположенные симметрично относительно центра на расстоянии 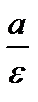 от него, называются директрисами эллипса.
от него, называются директрисами эллипса.
Если эллипс задан каноническим уравнением (8), то уравнения директрис имеют вид
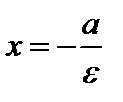 и
и 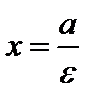 . (12)
. (12)
Так как 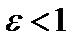 , то
, то 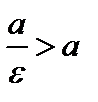 . Откуда заключаем, что правая директрисарасположена правее правой вершины эллипса, а левая – левее его левой вершины. Важность понятия директрис будет установлена позднее.
. Откуда заключаем, что правая директрисарасположена правее правой вершины эллипса, а левая – левее его левой вершины. Важность понятия директрис будет установлена позднее.
Гипербола
Гиперболой называется множество точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек 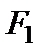 и
и 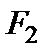 , называемых фокусами, есть величина постоянная, равная
, называемых фокусами, есть величина постоянная, равная 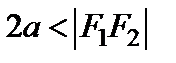 .
.
Пусть 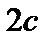 – расстояние между фокусами
– расстояние между фокусами 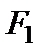 и
и 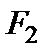 . Выберем декартову систему координат
. Выберем декартову систему координат 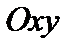 так, чтобы
так, чтобы 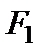 и
и 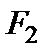 находились на оси
находились на оси 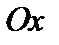 симметрично относительно начала координат (рис. 2).
симметрично относительно начала координат (рис. 2).
Если 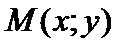 – произвольная точка гиперболы, то, по определению,
– произвольная точка гиперболы, то, по определению,
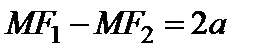 или
или 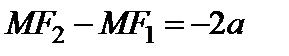 .
.

| Рис. 2 |
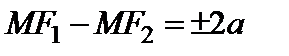 .
.
Отметим, что  , так как из треугольника
, так как из треугольника 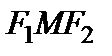 имеем
имеем 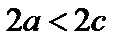 .
.
Рассуждая аналогично, как и при выводе канонического уравнения эллипса, получим каноническое уравнение гиперболы
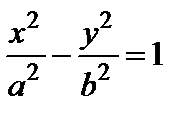 , где
, где 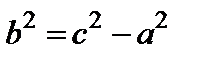 .(
.(
6.Парабола
Параболой называется множество точек плоскости, равноудаленных от данной точки F, называемой фокусом, и от данной прямой L, называемой директрисой.
Для вывода канонического уравнения параболы выберем декартову систему координат Оху так, чтобы ось Ох проходила через фокус F перпендикулярно директрисе, а начало координат О поместим на одинаковых расстояниях от фокуса и директрисы (рис.3).
2 LnhtbFBLAQItAAoAAAAAAAAAIQDpuymjmFYAAJhWAAAUAAAAAAAAAAAAAAAAANsIAABkcnMvbWVk aWEvaW1hZ2UxLnBuZ1BLBQYAAAAABgAGAHwBAAClXwAAAAA= "> 
| Рис. 3 |
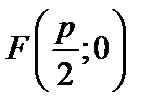 , а уравнением директрисы является
, а уравнением директрисы является 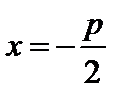 .
. Пусть М(х;у) – произвольная точка параболы. Тогда, согласно ее определению, имеем
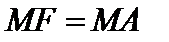 . (18)
. (18)
Точка А имеет координаты 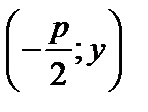 . Имеем
. Имеем
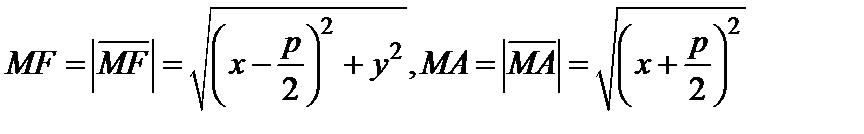 . (19)
. (19)
Из (18) и (19) получаем
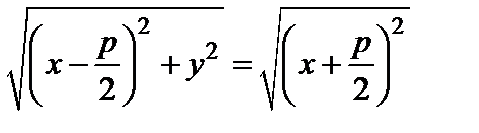 . (20)
. (20)
Отсюда 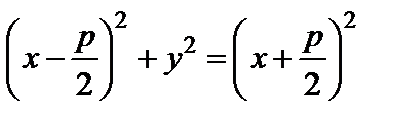 или
или 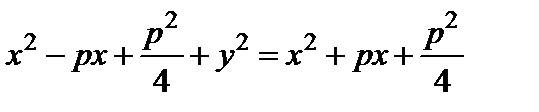 . Окончательно получаем
. Окончательно получаем
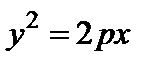 . (21)
. (21)
Уравнение (21) называется каноническим уравнением параболы, изображенной на рис. 3
