Понятие устойчивости и асимптотической устойчивости по Ляпунову

Рассмотрим систему дифференциальных уравнений

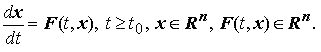
Полагаем, что выполнены условия теоремы существования и единственности решения задачи Коши.Пусть некоторое фиксированное решение x = φ(t) этой системы существует при всех t ≥ t0. Решение x = φ(t) системы называется асимптотически устойчивым по Ляпунову при t ≥ t0 , если :

— решение x = φ(t) устойчиво по Ляпунову при t ≥ t0 ;

— существует такое число Δ > 0, что любое решение x = φ(t), удовлетворяющее условию | x(t0) − φ(t0) | < Δ с ростом t стремится к нулю: | x(t0) − φ(t0) | → 0 при t → ∞. .

Геометрически это означает, что интегральные кривые x = x(t), близкие в момент t = t0 к интегральной кривой x = φ(t), приближаются к ней с ростом t.

Интегральные кривые и фазовые траектории, отвечающие асимптотически устойчивым решениям, тоже называются асимптотически устойчивыми.

На рисунке чёрным изображена асимптотически устойчивая фазовая траектория, некой системы дифференциальных уравнений второго порядка, которая начинается в точке (0.3, 0), и две, начинающиеся вблизи неё, траектории.

Типы точек покоя

Пусть имеем систему двух линейных однородных дифференциальных уравнений с постоянными коэффициентами причем

(1)

Причём

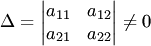
Точка 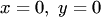, в которой правые части уравнений системы (1) обращаются в ноль, называется точкой покоя системы (1).

Для исследования точки покоя системы (1) надо составить характеристическое уравнение

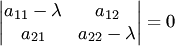(2)

и найти его корн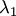и и .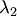

Возможны следующие случаи.

1. Корни 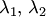характеристического уравнения (2) вещественные и разные:

а) 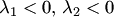. Точка покоя асимптотически устойчива (устойчивый узел, рис. 32);

б) 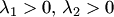. Точка покоя неустойчива (неустойчивый узел, рис. 33);

в) 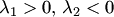. Точка покоя неустойчива (седло, рис. 34).

2. Корни характеристического уравнения (2) комплексные: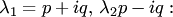

а) 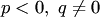. Точка покоя асимптотически устойчива (устойчивый фокус, рис.35);

б) 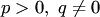. Точка покоя неустойчива (неустойчивый фокус, рис.36);

в) 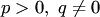. Точка покоя устойчива (центр, рис. 37).

3. Корни 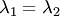кратные:

а) 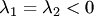. Точка покоя асимптотически устойчива (устойчивый узел, рис.38, 39);

б) 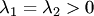. Точка покоя неустойчива (неустойчивый узел, рис.40, 41).

Теорема. Если все корни характеристического уравнения для системы (6) имеют отрицательную вещественную часть, то точка покоя системы (6) 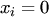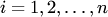, асимптотически устойчива. Если хотя бы один корень характеристического уравнения имеет положительную вещественную часть, то точка покоя неустойчива.

Числовой ряд сумма ряда

ЧИСЛОВОЙ РЯД – бесконечная сумма членов бесконечной числовой последовательности {an} называется числовым рядом:

a1 + a2+ a3 + … + an+ … = .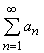

Каждому натуральному n сопоставляется сумма первых n членов последовательности {an}

S1 = a1, S2= a1 + a2, …, Sn = 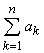= a1 + a2 + a3 + … + an, …

Значения Sn называют частичными суммами ряда. Они образуют последовательность {Sn} последовательность частичных сумм (бесконечного) ряда an – общий член ряда.

Если последовательность частичных сумм данного ряда имеет предел S,то есть

,

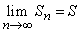то ряд сходится и S – его сумма. Записывается это следующим образом:

a1 + a2 + a3 + … + an + … = S, или 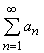= S.

В противном случае ряд называют расходящимся.

Таким образом, сумма ряда – это, по определению, предел последовательности его частичных сумм.

Пусть есть геометрическая прогрессия bn = b1qn–1, знаменатель которой qпо абсолютной величине меньше единицы (–1 < q < 1). Вычислим сумму первых n членов геометрической прогрессии:

Sn= b1+ b1qn + b1q2 + …+ b1qn–1= .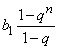

Очевидно, что при |q| < 1 с ростом n значение qn стремится к нулю. Тогда значение Sn стремится к 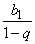и это число называется суммой всех членов бесконечной убывающей геометрической прогрессии: b1 + b1qn + b1q2 + …= .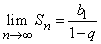