Метод вариации производных постоянных

Рассмотрим ЛНДУ (5.1). Его общим решением является функция (5.3), т. е.

Частное решение уравнения (5.1) можно найти, если известно общее решение соответствующего однородного уравнения (5.2), методом вариации произвольных постоянных (метод Лагранжа), состоящим в следующем. Пусть 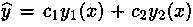общее решение уравнения (5.2).Заменим в общем решении постоянные c1 и с2 неизвестными функциями c1(x) и с2(х) и подберем их так, чтобы функция

была решением уравнения (5.1). Найдем производную

Подберем функции c1(x) и с2(х) так, чтобы

Тогда

Подставляя выражение для в уравнение (5.1), получим:

или

Поскольку y1(x) и у2(х) - решения уравнения (5.2), то выражения в квадратных скобках равны нулю, а потому

Таким образом, функция (5.6) будет частным решением у* уравнения (5.1), если функции c1(x) и с2(х) удовлетворяют системе уравнений (5.7) и (5.8):

Определитель системытак как это определитель Вронского для фундаментальной системы частных решений у1 (х) и у2 (х) уравнения (5.2). Поэтому система (5.9) имеет единственное решение: с'1(х)= j1(x) и с'2(х)=j2(х), где j1(x) и j2(х) - некоторые функции от х. Интегрируя эти функции, находим c1(x) и с2(х), а затем по формуле (5.6) составляем частное решение уравнения (5.1).

Пример 5.1. Найти общее решение уравнения

Решение: Найдем общее решение соответствующего однородного уравнения Имеем:Следовательно,

Найдем теперь частное решение у* исходногоуравнения. Оно ищется в виде (5.6): Для нахождения с1(х) и с2(х) составляем систему уравнений вида (5.9):

Решаем ее:

Запишем частное решение данного уравнения: Следовательно, общее решение данного уравнения имеет вид

При нахождении частных решений ЛНДУ может быть полезной следующая теорема.

Теорема 5.2 (о наложении решений). Если правая часть уравнения (5.1) представляет собой сумму двух функций: - частные решения уравнений соответственно, то функция у*=y*1+y*2 является решением данного уравнения.

Действительно,

Неоднородные линейные уравнения высших порядков

Системы ду. Нормальная система

Определение 1. Нормальная система обыкновенных дифференциальных уравнений имеет следующий вид:

(1.1)

где , – неизвестные функции от независимой переменной x, подлежащие определению; , – известные функции от , заданные и непрерывные в некоторой области. Число n называется порядком системы (1.1). В дальнейшем ограничимся рассмотрением систем второго порядка (n=2).

Определение 2. Пусть дана нормальная система уравнений

(1.2)

где и – заданные и непрерывные в некоторой области функции. Пара функции (y(x); z(x)), определенная на (a,b), имеющая непрерывные производные и удовлетворяющая на (a,b) обоим уравнениям системы (1.2), называется ее решением.

Задача нахождения решения (y(x); z(x)), удовлетворяющего начальным условиям , где – заданные числа (начальные данные), называется задачей Коши.

Геометрический смысл решения системы ДУ

Интегрирование систем ДУ

Системы дифференциальных уравнений n–го порядка можно решать сведением к уравнению n–го порядка. Такой метод решения систем называетсяметодом исключения.

Рассмотрим, например, нормальную систему дифференциальных уравнений 2 –го порядка

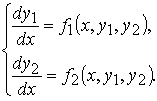
Исключим функцию y₂. Для этого сначала выразим y₂ через x и y₁ из первого уравнения системы , затем продифференцируем по x первое уравнение системы, заменяя y₂ полученным для него выражением, а производную y₂ − правой частью второго уравнения системы:

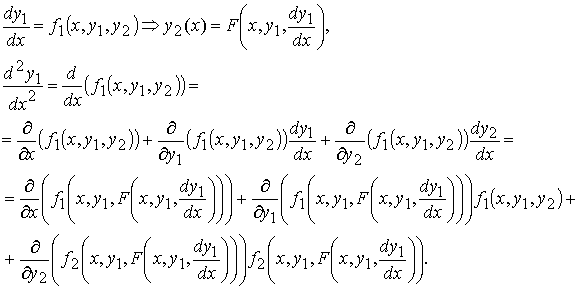
Получили обыкновенное дифференциальное уравнение 2 –го порядка

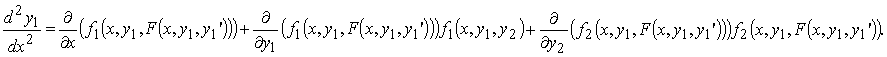
Таким же образом решают методом исключения произвольные системы n–го порядка: дифференцируют уравнения системы и, последовательно исключая функции y₂, ..., y_n и их производные, сводят систему к одному дифференциальному уравнению n–го порядка относительно y₁.