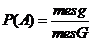Схема независимых испытаний Бернулли. Формула Бернулли

Если производится несколько испытаний причём вероятность события А в каждом испытании независит от исходов др. испытаний, то такие испытания называются независимыми относительно А. Например: бросание игральной кости.

Теор: вероятность того что в n-независимых испытаниях в каждом из которых вероятность появления события равна р(0<р<1) событие наступит ровно к раз безразлично в какой последовательности, определятся по формуле

Док: в формуле подразумевается что А появится к-раз безразлично в какой последовательности, вероятность сложного события, что А наступит к раз, и не наступит n-k раз определяется по формуле: , но таких испытаний может быть несколько, а именно события эти несовместны.

Нормальное распределение вероятностей непрерывных СВ.

Опр.: Говорят, что НСВ распределена по норм. Закону с параметрами а,σ, если плотность распределения имеет вид:

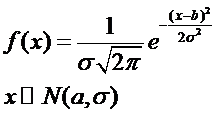
Вероятность попадания СВ в интервал [α,B]: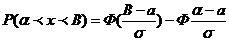

Правило 3-х сигм.

Если СВ , тогда справедлива формула:

Состоятельность несмещенность и эффективность оценок

Состоятельность характеризует сходимость по вероятности оценки q к истинному значению параметра T при неограниченном увеличении объема выборки n. Для состоятельности оценки достаточно, но не обязательно, чтобы математическое ожидание квадрата отклонения оценки от параметра M(T – q )2 стремилось к нулю с увеличением объема выборки (здесь и далее символ М означает математическое ожидание).

Несмещенность характеризует отсутствие систематических (в среднем) отклонений оценки от параметра при любом конечном, в том числе и малом, объеме выборки, т. е. M(q ) =T. Использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, приводит к систематическим ошибкам. Эффективностьхарактеризует разброс случайных значений оценки около истинного значения параметраДля многих применяемых способов оценивания выборочные распределения параметров асимптотически нормальны, поэтому часто мерой эффективности служит дисперсия оценки. В таком понимании эффективная оценка – это оценка с минимальной дисперсией.

Билет 5.

1. Классическое, геометрическое, аксиоматическое и статистическое определение вероятностей.

Вероятность события – математическая оценка возможности появление случайного события в результате опыта.

Если m- число событий благоприятствующих событию A, то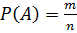

Свойство вероятностей события А:

1.

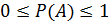
2.

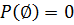
3.

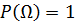
4. А,В – несовместные P(A+B)=P(A)+P(B)

Пусть происходит эксперимент и событие А появляется в М из N, тогда 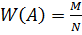– относительная частота события.

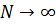- остаётся примерно постоянным.

Статистическое определение вероятности заключается в том что за вероятность события А принимается её относительная частота.

Аксиоматическое определение вероятности: вероятность события А это функция Р(А) удовлетворяющая след. свойствам:

1. P(∅)=0

2. P(Ω)=1

3. 0≤P(A)≤1

4. Ai – несовместное событие i=1,..,n то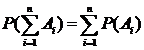

Геометрическое определение