Простейшие функции и их графики

Пропорциональные величины. Если переменные величины у и х (прямо) пропорциональны, то функциональная зависимость между ними выражается уравнением y = kx, где k есть некоторая постоянная величина (коэффициент пропорциональности). График прямой пропорциональности есть прямая линия (см. приложение 1), проходящая через начало координат и образующая с осью абсцисс угол α, тангенс, которого равен постоянной k; tg α = k. Поэтому коэффициент пропорциональности k называется также угловым коэффициентом.

Линейная функция. Линейной называется функция вида: y = kx + b, в аналитическое выражение, которой переменные х и у входят в первой степени. График линейной функции представляет прямую линию (см. приложение 2), располагающеюся относительно координатных осей различным образом, в зависимости от постоянных коэффициентов, k и b, которые могут принимать положительные или отрицательные значения или быть равным нулю. Для построения графика линейной функции можно воспользоваться геометрическим смыслом коэффициентов k и b или найти две точки прямой на плоскости, например, точки пересечения с осями координат.

Свойства функции y = kx+b:

D(f) = (- + );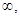

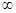Возрастает, если k >0, убывает, если k<0;

Не ограничена ни сверху, ни снизу;

Нет ни наибольшего, ни наименьшего значений;

Функция непрерывна;

E(f) = (- + );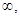

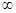Обратная пропорциональность. Если переменные величины у и х обратно пропорциональны, то функциональная зависимость между ними выражается уравнением 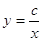, где с есть некоторая постоянная величина. График обратной пропорциональности есть кривая линия , называемая гиперболой, состоящая из двух ветвей.

Свойства функции :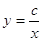

D(f) = (- 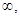0) U (0, + );

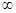Если с >0, то функция убывает на открытом луче (- 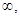0) и на открытом луче (0, + 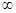); если с<0, то функция возрастает на (- 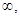0) и на (0, + );

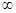Не ограничена ни снизу, ни сверху;

Нет ни наименьшего, ни наибольшего значений;

Функция непрерывна на открытом луче (- 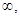0) и на открытом луче (0, + );

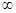Е(f) = (- 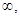0) U (0, + );

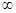Если с>0, то функция выпукла вверх при х<0, т.е. на отрытом луче (- 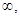0), и выпукла вниз при х>0, т.е. на открытом луче (0, + 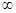). Если с<0, то функция выпукла вверх при х>0 и выпукла вниз при х<0;

Функция имеет асимптоты y = 0 и x = 0/

Квадратичная функция. Функция y = ax2 + bx + с (a, b, с - постоянные величины; а ≠ 0) называется квадратичной. В простейшем случае y = ax2 (b = с = 0) график есть кривая линия, проходящая через начало координат. Кривая, служащая графиком функции y = ax2, есть парабола (см. приложение 4). Каждая такая парабола имеет ось симметрии (OY), называемую осью параболы. Точка О пересечения параболы с ее осью называется вершиной параболы. График функции y = ax2 + bx + с имеет ту же формулу, что и график функции y = ax2 (при том же значении а), т.е. также есть парабола. Ось этой параболы по-прежнему вертикальна, но вершина лежит не в начале координат, а в точке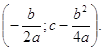

Свойства функции ax2 + bx + с:

Для случая, а>0

D(f) = (- + );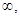

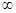Убывает на луче 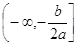, возрастает на луче ;

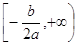Ограничена снизу, не ограничена сверху;

унаим. = y0, yнаиб. Не существует;

Непрерывна;

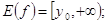
Выпукла вниз.

Для случая, а<0

D(f) = (- + );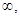

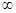Убывает на луче 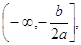возрастает на луче ;

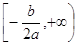Не ограничена снизу, ограничена сверху;

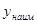не существует, yнаиб. = y0;

Непрерывна;

6.

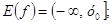
Выпукла вверх.

Свойства функции y = ax2:

Для случая, а>0

D(f) = (- + );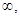

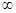Убывает на луче 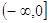, возрастает на луче ;

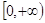Ограничена снизу, не ограничена сверху;

унаим. = 0, yнаиб. Не существует;

Непрерывна;

E(f) = ;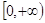

Выпукла вниз.

Для случая, а<0

D(f) = (- + );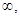

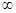Убывает на луче 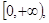возрастает на луче ;

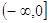Не ограничена снизу, ограничена сверху;

унаим. Не существует, yнаиб. = 0;

Непрерывна;

E(f) =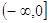

Выпукла вверх.

Степенная функция. Обычно степенными функциями называют функции вида 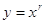, где r - любое действительное число. Так, если r - натуральное число (r = n), то получаем функцию .

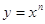График степенной функции y = xn в случае четного n (n = 4, 6,8, …) похож на параболу, а график степенной функции y = xn в случае нечетного n (n = 5, 7, 9, …) похож на кубическую параболу.

Если r = - n, то получаем функцию y = x - n, т.е. .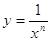

Наконец, если r = 0, т.е. речь идет о функции y = x0, то в результате получается обыкновенная функция у = 1, где х ≠ 0; график этой функции изображен (см приложение 6).

Теперь рассмотрим функцию y = xr, где r - положительное или отрицательное дробное число. Рассмотрим в качестве примера функцию y = x2,5. Область ее определения - луч 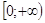. Построим на этом луче графики функций у = х2 (ветвь параболы) и у = х3 (ветвь кубической параболы) - эти графики изображены. Стоит заметить, что на интервале (0;

1) кубическая парабола располагается ниже, а на открытом луче (1; +∞) выше параболы. Нетрудно убедиться в том, что график функции у = х2,5 проходит через точки (0; 0) и (1;

1), как и графики функций у = х2, у = х3. При остальных значениях аргумента х график функции у = х2,5 находится между графиками функций у = х2 и у = х3 (см. приложение 7).

Почему так происходит? Посмотрим:

1). Если 0 < х < 1, то 2). Если х > 1, то

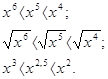
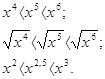
Примерно так же обстоит дело для любой степенной функции вида у = хr, где 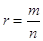-неправильная дробь(числитель больше знаменателя). Ее графиком является кривая (см. приложение 8), похожая на ветвь параболы. Чем больше показатель r, тем “круче” устремлена эта кривая вверх.

Свойства функции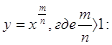

D(f) = ;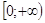

не является ни четной, ни нечетной;

возрастает на ;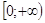

не ограничена сверху, ограничена снизу;

не имеет наибольшего значения; у наим. = 0;

непрерывна;

E(f) = ;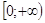

выпукла вниз.

Рассмотрим степенную функцию 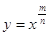для случая, когда 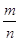- правильная дробь 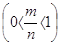. Все рассмотренное в этой главе в отношении функции 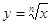, или, что то же самое, 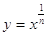имеет и отношению к любой степенной функции вида у = хr, где 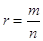- правильная дробь. График этой функции изображен (см. приложение 9)

Свойства функции 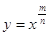, где :

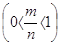D(f) = ;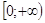

не является ни четной, ни нечетной;

возрастает на ;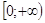

не ограничена сверху, ограничена снизу;

не имеет наибольшего значения; у наим. = 0;

непрерывна;

E(f) = ;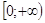

выпукла вверх.

Нам осталось рассмотреть степенную функцию вида 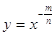. Область ее определения - открытый луч 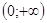. Выше мы построили график степенной функции y = x - n, где n - натуральное число. При 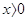график функции y = x - n похож на ветвь гиперболы. Точно так же дело обстоит для любой степенной функции вида 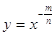график, которой изображен. Отметим, что график данной функции имеет горизонтальную асимптоту y = 0 и вертикальную асимптоту x = 0.

Свойства функции :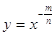

D(f) = ;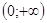

не является ни четной, ни нечетной;

возрастает на ;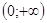

не ограничена сверху, ограничена снизу;

не имеет ни наибольшего значения, ни наименьшего значения;

непрерывна;

E(f) = ;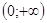

выпукла вниз.

Функция 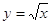. Графиком функции является ветвь параболы (см. приложение 10).

Свойства функции :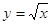

D(f) =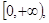

Возрастает;

Ограничена снизу, не ограничена сверху;

у наим. = 0, yнаиб. = Не существует;

Непрерывна;

E(f) = ;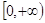

Выпукла вверх.

7. Функция 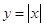. Графиком функции является объединение двух лучей: у = х, х≥0 и

у = - х, х≤0 (см. приложение 11).

Свойства функции .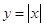

D(f) = (- + );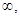

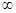Убывает на луче 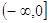, возрастает на луче ;

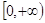Ограничена снизу, не ограничена сверху;

унаим. = 0, yнаиб. Не существует;

Непрерывна;

E(f) = ;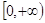

Выпукла вниз.

2.2 Кривые второго порядка

В предыдущем параграфе было установлено, что всякая прямая в прямоугольной системе координат Оху определяется уравнением первой степени относительно переменных х и у. Так же было установлено, всякое уравнение первой степени ах + bу + с = 0 в прямоугольной системе координат определяет прямую и притом единственную, если а² + b² ¹ 0. В настоящей главе мы займемся изучением линий определяемых уравнениями второй степени относительно текущих координат х и у:

ах² + 2bху + су² + 2dх + 2eу + f = 0 (1)

Такие линии называют линиями (кривыми) второго порядка. Коэффициенты уравнения (1) могут принимать различные действительные значения, исключая одновременное равенство а, b и c нулю (в противном случае уравнение (1) не будет уравнением второй степени).Эллипс.

Эллипсом называют множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек той же плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Составим уравнение эллипса с фокусами в данных точках F1 и F2. Для этого выберем прямоугольную систему координат так, чтобы ось Ох проходила через фокусы, а начало координат делило отрезок F1F2 пополам (см. приложение 14). Обозначив F1F2 = 2с, получим F1(с; 0) и F2(-с; 0). Пусть М(х; у) - произвольная точка эллипса.

Расстояние r1 = F1M и r2 = F2M называются фокальными радиусами точки М.

Положим r1 + r2 = 2а; (1)

Тогда согласно определению эллипса 2а - величина постоянная, причем 2а>2с, т.е. а>c.

По формуле расстояния между двумя точками находим

r1 = 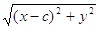и r2 =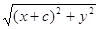

Подставим найденные значения r1 и r2 в равенство (1) получим уравнение эллипса

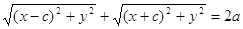
После несложных преобразований уравнение примет вид

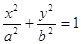(2)

Уравнение (2) называется каноническим уравнением эллипса.

Исследование:

Координаты точки О(0; 0) не удовлетворяют уравнению (2), поэтому эллипс, определяемый этим уравнением, не проходит через начало координат.

Найдем точки пересечения эллипса с осями координат. Положив в уравнении (2) у = 0, найдем х = ± а. Следовательно, эллипс пересекает ось Ох в точках А1(а; 0) и А2(-а; 0). Аналогично получаем точки пересечения эллипса с осью Оу: В1(0; b) и B2(0; - b)

D(y) Î [-a; a]

E(y) Î [-b; b]

При возрастании ½х½ от 0 до а величина ½у½ убывает от b до 0, а при возрастании ½у½от 0 до b величина ½х½ убывает от а до 0.

Частным случаем эллипса является окружность, где а = b.

Окружность

Как известно, окружностью называют множество всех точек плоскости, одинаково удаленных от данной точки, называемой центром.

Пусть дана окружность радиусом r с центром в точке О1(a; b) (см. приложение 15); требуется составить ее уравнение.

Возьмем на данной окружности произвольную точку М (х; у)

Имеем: О1М = r, т.е.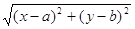

Откуда (х-а) ² + (у - b) ² = r² (1)

Итак, уравнению (1) удовлетворяют координаты произвольной точки окружности. Более того, этому уравнению не удовлетворяют координаты никакой точки, не лежащей на окружности, так как если

О1М< r, то (х-а) ² + (у - b) ² < r²,

и если

О1М> r, то (х-а) ² + (у - b) ² > r².

Следовательно, (1) Есть уравнение окружности радиусом r с центром в точке О1(a; b). Если центр окружности находится на оси Ох, т.е. если b = 0, то уравнение (1) примет вид

(х-а) ² + у² = r²

Если центр окружности находится на оси Ох, т.е. если b = 0, то уравнение (1) примет вид

х² + (у - b) ² = r²

Наконец, если центр окружности находится в начале координат, т.е. если а = b = 0, то уравнение примет (1) вид

х² + у² = r²

Если в уравнении (1) раскрыть скобки, перенести все члены в левую часть и расположить их по степеням х и у, то получим

x² + y² - 2ax - 2by + a² + b² - r² = 0

Отсюда следует, что уравнение окружности является уравнением второй степени относительно переменных х и у, как бы она ни была расположена в плоскости Оху.

В этой главе были рассмотрены основные простейшие функции, кривые второго порядка и тригонометрические функции, так же представлены их графики.