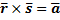Параметрическое уравнение плоскости

Пусть в координатном пространстве 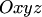заданы:

а) точка ;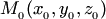

б) два неколлинеарных вектора (рис.4.15).

Требуется составить параметрическое уравнение вида (4.10) плоскости, компланарной векторам 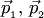и проходящей через точку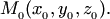

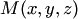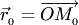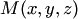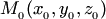Выберем на плоскости произвольную точку . Обозначим -радиус-векторы точек и (рис.4.16).

Точка 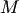принадлежит заданной плоскости тогда и только тогда, когда векторы и 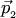компланарны . Запишем условие компланарности: где 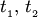— некоторые действительные числа (параметры). Учитывая, что 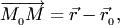получим векторное параметрическое уравнение плоскости:

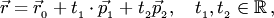
где 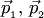— направляющие векторы плоскости, а — радиус-вектор точки, принадлежащей плоскости.

Координатная форма записи уравнения называется параметрическим уравнением плоскости:

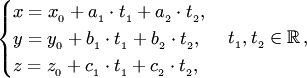
где и — координаты направляющих векторов и 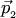соответственно. Параметры 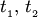в уравнениях , имеют следующий геометрический смысл: величины 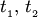пропорциональны расстоянию от заданной точки 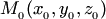до точки принадлежащей плоскости. При точка 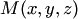совпадает с заданной точкой 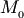. При возрастании (или ) точка 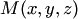перемещается в направлении вектора (или 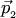), а при убывании (или ) — в противоположном направлении.

35)A * x + B * y + C * Z = D – координатное уравнение плоскости или общее уравнение плоскости

36) x/a + y/b + z/c = 1 – уравнение плоскости . Где а , b, с это отрезки , которые отсекают плоскость на координатные оси.

Параллельность плоскостей

Классическое определение

Две плоскости называются параллельными, если они не имеют общих точек.

Необходимым и достаточным условием параллельности или совпадения плоскостей (4.23) является условие коллинеарности их нормалей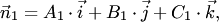

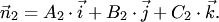
Свойства и признаки

§ Если плоскость α параллельна каждой из двух пересекающихся прямых, лежащих в другой плоскости β, то эти плоскости параллельны

§ Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны

§ Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну

§ Отрезки параллельных прямых, ограниченные двумя параллельными плоскостями, равны

§ Два угла с соответственно параллельными и одинаково направленными сторонами равны и лежат в параллельных плоскостях

38)Необходимым и достаточным условием параллельности или совпадения плоскостей является условие коллинеарности их нормалей 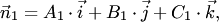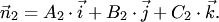Следовательно, если плоскости (4.23) параллельны или совпадают, то 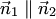т.е. существует такое число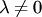

39) Необходимым и достаточным условием пересечения двух плоскостей (4.22) является условие неколлинеарности их нормалей, или, что то же самое, условие непропорциональности коэффициентов при неизвестных:

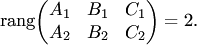
(4.25)

При этом условии система уравнений:

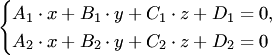
имеет бесконечно много решений, которые определяют прямую пересечения плоскостей, заданных уравнениями (4.23).

Угол между плоскостями

Необходимым и достаточным условием перпендикулярности плоскостей (4.23) является условие ортогональности их нормалей, т.е.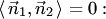

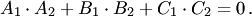
40.Условие ортогональности 2-х плоскостей.
две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, 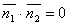или .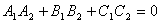

Таким образом, .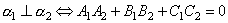
41.Задача о вычислении угла, образованного пересекающимися плоскостями

Две пересекающиеся плоскости образуют две пары смежных углов. Меньший из смежных углов называется углом между плоскостями.

Пусть пересекающиеся плоскости заданны следующими уравнениям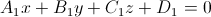и:

и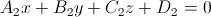

тогда угол между плоскостями вычисляется по следующей формуле:

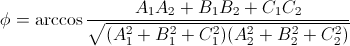
42.Векторно-параметрическое уравнение прямой в пространстве.
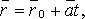где 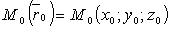- фиксированная точка, лежащая на прямой; 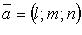- направляющий вектор.

В координатах (параметрические уравнения):

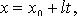
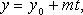
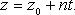
43.Каноническое уравнение прямой в пространстве.

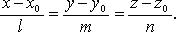
44.Векторное уравнение прямой в пространстве.
;
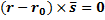