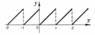Основные действия над матрицами

Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.

Определение. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.

Определение. Матрица вида:

= E,

называется единичной матрицей.

Определение. Если amn = anm , то матрица называется симметрической.

Пример. - симметрическая матрица

Определение. Квадратная матрица вида называется диагональной матрицей.

Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:

Определение. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.

cij = aij ± bij

С = А + В = В + А.

Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.

a (А+В) =aА ± aВ

А(a±b) = aА ± bА

Пример. Даны матрицы А = ; B = , найти 2А + В.

2А = , 2А + В = .

Операция умножения матриц

Определение: Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:

A×B = C;

Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.

Свойства операции умножения матриц.

1)Умножение матриц не коммутативно, т.е. АВ ¹ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.

Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.

Перестановочными могут быть только квадратные матрицы одного и того же порядка.

А×Е = Е×А = А

Очевидно, что для любых матриц выполняются следующее свойство:

A×O = O; O×A = O,

где О – нулевая матрица.

2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:

(АВ)С=А(ВС).

3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно:

А(В + С) = АВ + АС

(А + В)С = АС + ВС.

4) Если произведение АВ определено, то для любого числа a верно соотношение:

a(AB) = (aA)B = A(aB).

5) Если определено произведение АВ , то определено произведение ВТАТ и выполняется равенство:

(АВ)Т = ВТАТ, где

индексом Т обозначается транспонированная матрица.

6) Заметим также, что для любых квадратных матриц det (AB) = detA×detB.

13 ВОПРОС:

Если число строк матрицы равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными матрицами.

Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю. Транспонированием называется такое преобразование матрицы, при котором строки и столбцы меняются местами с сохранением их номеров. Обозначается транспонирование значком Т наверху.

Пусть дана матрица (4.1). Переставим строки со столбцами. Получим матрицу

AT = ,

которая будет транспонированной по отношению к матрице А. В частности, при транспонировании вектора-столбца получается вектор-строка и наоборот.

Произведением матрицы А на число λ называется матрица, элементы которой получаются из соответствующих элементов матрицы А умножением на число λ: λA = ( λaij).

Суммой двух матриц А = (aij) и B = (bij) одного размера называется матрица C = (cij) того же размера, элементы которой определяются по формуле cij = aij + bij.

Произведение АВ матрицы А на матрицу В определяется в предположении, что число столбцов матрицы А равно числу строк матрицы В.

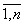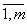Произведением двух матриц А = (aij) и B = (bjk), где i = , j= , k= 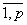, заданных в определенном порядке АВ, называется матрица С = (cik), элементы которой определяются по следующему правилу:

cik = ai1b1k + ai2b2k + ... + aimbmk = aisbsk. (4.2)

Иначе говоря, элементы матрицы-произведения определяются следующим образом: элемент i-й строки и k-го столбца матрицы С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца матрицы В.

Пусть нам дана квадратная матрица порядка n

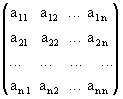. (4.3)

Рассмотрим все возможные произведения по n элементов этой матрицы, взятых по одному и только по одному из каждой строки и каждого столбца, т.е. произведений вида:

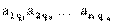, (4.4)

где индексы q1, q2,..., qn составляют некоторую перестановку из чисел

1, 2,..., n. Число таких произведений равно числу различных перестановок из n символов, т.е. равно n!. Знак произведения (4.4) равен (- 1)q, где q - число инверсий в перестановке вторых индексов элементов.

Определителем n -го порядка, соответствующим матрице (4.3), называется алгебраическая сумма n! членов вида (4.4). Для записи определителя употребляется символ ‌ A ‌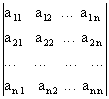 = или det A= 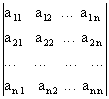(детерминант, или определитель, матрицы А).

14 ВОПРОС:

Метод Гаусса:

Наиболее известным и популярным точным способом решения систем линейных алгебраических уравнений (СЛАУ) является метод Гаусса. Этот метод заключается в последовательном исключении неизвестных. Пусть в системе уравнений

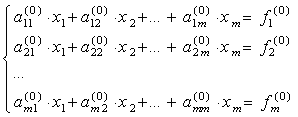
первый элемент a11(0) не равен 0. Назовем его ведущим элементом первой строки. Поделим все элементы этой строки на a11(0) и исключим x1 из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при x1 в соответствующей строке. Получим

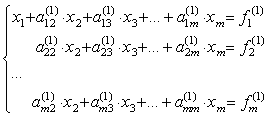
Если a22(1), то, продолжая аналогичное исключение, приходим к системе уравнений с верхней треугольной матрицей

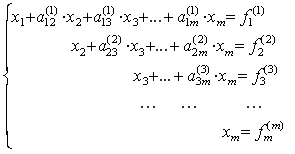
Из нее в обратном порядке находим все значения xi:

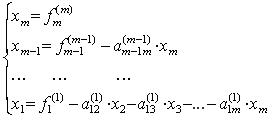
Процесс приведения к системе с треугольной матрицей называется прямым ходом, а нахождения неизвестных - обратным. Если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Тем не менее, для нормальной матрицы с ненулевым определителем всегда возможна такая перестановка уравнений, что на главной диагонали не будет нулей. В приведенном коде для простоты перестановок не делается, зато делается проверка решения, а прямой и обратный ход для наглядности вынесены в отдельные подпрограммы.

Метод Крамера:

Для системы n линейных уравнений с n неизвестными (над произвольным полем)

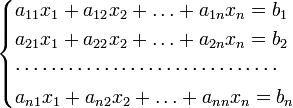
с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде

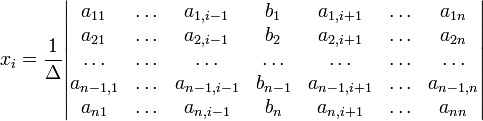
(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

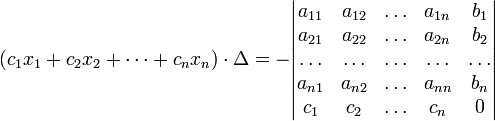
В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b₁,b₂,...,b_n и x₁,x₂,...,x_n, либо набор c₁,c₂,...,c_n состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

15 ВОПРОС:

Определение:

Числовая последовательность — это последовательность элементов числового пространства.

Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе.

Предел:

Предел последовательности — это объект, к которому члены последовательности приближаются с ростом номера. Так в произвольном топологическом пространстве пределом последовательности называется элемент, в любой окрестности которого лежат все члены последовательности, начиная с некоторого. В частности для числовых последовательностей предел — это число, в любой окрестности которого лежат все члены последовательности начиная с некоторого.

Частичный предел последовательности — это предел одной из её подпоследовательностей. У сходящихся числовых последовательностей он всегда совпадает с обычным пределом.

Верхний предел последовательности — это наибольшая предельная точка этой последовательности.

Нижний предел последовательности — это наименьшая предельная точка этой последовательности.

Теорема Вейерштрасса. Всякая монотонная и ограниченная последовательность имеет предел (эта теорема даётся в средней школе без доказательства).

Основные свойства пределов. Нижеприведенные свойства пределов справедливы не только для числовых последовательностей, но и для функций.

Если { un } и { vn } - две сходящиеся последовательности, то:

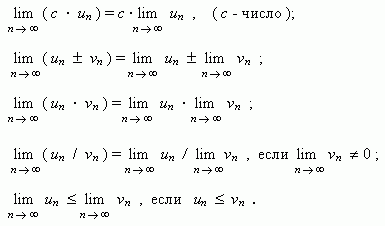
Если члены последовательностей { un }, { vn }, { wn } удовлетворяют неравенствам

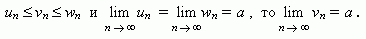
Некоторые замечательные пределы.

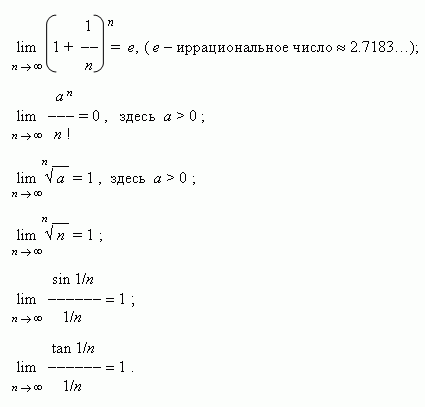
16 ВОПРОС:

Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.

Определение предела по Гейне. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности 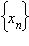такой, что 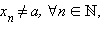сходящейся к числу a, соответствующая последовательность значений функции 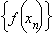сходится к числу A.

Основные теоремы о пределах

Теорема 1.(о единственности предела функции). Функция не может иметь более одного предела.

Следствие. Если две функции f(x) и g(x) равны в некоторой окрестности точки 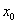, за исключением, может быть, самой точки 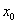, то либо они имеют один и тот же предел при 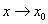, либо обе не имеют предела в этой точке.

Теорема 2.Если функции f(x) и g(x) имеют пределы в точке 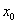, то:

1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.

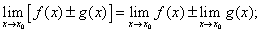(2)

2) предел произведения функций равен произведению пределов сомножителей, т.е.

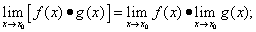(3)

3)предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.

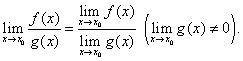(4)

Замечание.Формулы (2) и (3) справедливы для любого конечного числа функций.

Следствие 1.Предел постоянной равен самой постоянной, т.е.

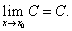
Следствие 2.Постоянный множитель можно выносить за знак предела, т.е.

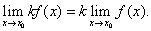
17 ВОПРОС:

Определение 2.11 Первым замечательным пределом называется предел

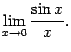
Теорема 2.14 Первый замечательный предел равен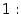

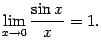
Доказательство. Рассмотрим два односторонних предела 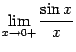и 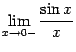и докажем, что каждый из них равен 1. Тогда по теореме 2.1 двусторонний предел 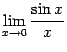также будет равняться 1.

Итак, пусть 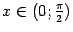(этот интервал -- одно из окончаний базы 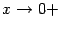). В тригонометрическом круге (радиуса 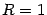) с центром 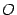построим центральный угол, равный , и проведём вертикальную касательную в точке 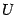пересечения горизонтальной оси с окружностью ( 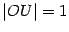). Обозначим точку пересечения луча с углом наклона с окружностью буквой 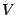, а с вертикальной касательной -- буквой 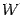; через 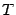обозначим проекцию точки 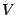на горизонтальную ось.

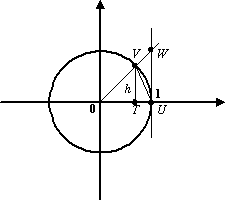
Рис.2.27.Тригонометрический круг

Пусть 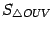-- площадь треугольника 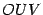, 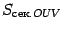-- площадь кругового сектор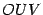а , а 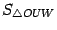-- площадь треугольника 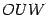. Тогда очевидно следующее неравенство:

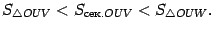
Заметим, что горизонтальная координата точки 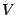равна 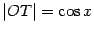, а вертикальная -- 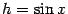(это высота треугольника 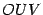), так что 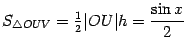. Площадь центрального сектора круга радиуса 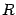с центральным углом равна 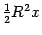, так что 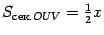. Из треугольника 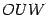находим, что 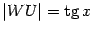. Поэтому 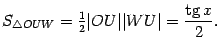Неравенство, связывающее площади трёх фигур, можно теперь записать в виде

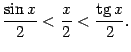
Все три части этого неравенства положительны, поэтому его можно записать так:

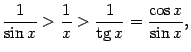
или (умножив на 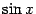) так:

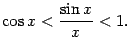
Предел постоянной 1 в правой части неравенства, очевидно, равен 1. Если мы покажем, что при 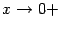предел 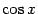в левой части неравенства тоже равен 1, то по теореме "о двух милиционерах" предел средней части 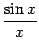также будет равен 1.

Итак, осталось доказать, что 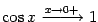. Сперва заметим, что 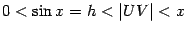, так как равняется длине дуги окружности 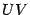, которая, очевидно, длиннее хорды 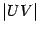. Применяя теорему "о двух милиционерах" к неравенству

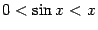
при 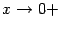, получаем, что

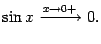(2.3)

Простая замена переменной 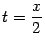показывает, что и 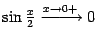. Теперь заметим, что 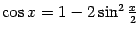. Применяя теоремы о линейности предела и о пределе произведения, получаем:

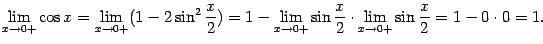(2.4)

Тем самым показано, что

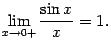
Сделаем теперь замену 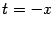; при этом база 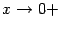перейдёт в базу 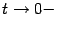(что означает, что если 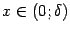, то 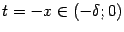). Значит,

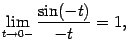
но 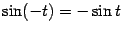( 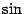-- нечётная функция), и поэтому

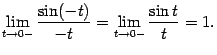
Мы показали, что левосторонний предел также равен 1, что и завершает доказательство теоремы.

Доказанная теорема означает, что график функции 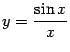выглядит так:

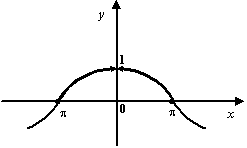
Рис.2.28.График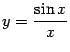

Приведём примеры применения первого замечательного предела для вычисления других родственных пределов.

Теорема 2.15 Второй замечательный предел существует. Его значение 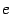-- число, лежащее между 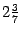и .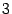

Более подробное изучение числа 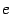показывает, что 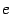-- иррациональное число, несколько первых десятичных знаков которого таковы:

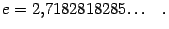
Для доказательства теоремы 2.15 нам понадобится следующая лемма; формула, в ней полученная, называется формулой бинома Ньютона.

Лемма 2.2 Пусть 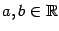и 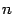-- натуральное число. Тогда имеет место формула

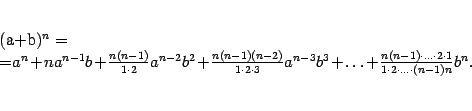
Заметим, что в дроби

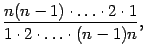
очевидно, сокращаются все сомножители в числителе и знаменателе, так что эта дробь равна 1. Аналогично, в предыдущем (не выписанном) слагаемом после сокращения получается коэффициент, равный 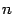, в третьем справа слагаемом -- равный 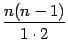, и т. д. Таким образом, коэффициенты в слагаемых, стоящих на одинаковых местах, считая слева и справа от края формулы, совпадают.

Доказательство. Доказывать утверждение леммы будем по индукции по параметру 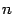. При 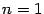формула 2.2, очевидно, верна:

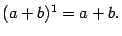
(Заметим, что пр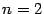и и 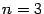формула 2.2 также хорошо известна:

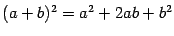
и

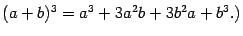
Предположим, что она верна для 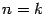, и докажем, что тогда она верна и при 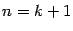. Действительно,

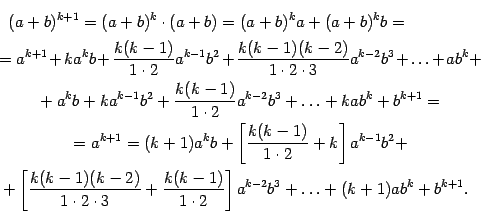
При этом в квадратных скобках получается:

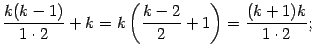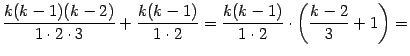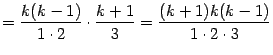и так далее, то есть как раз то, что должно получиться в качестве коэффициентов формулы бинома Ньютона при .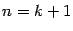

Доказательство теоремы 2.15. Рассмотрим последовательность 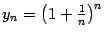и применим к 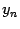формулу бинома Ньютона пр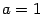и и 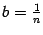. Получим

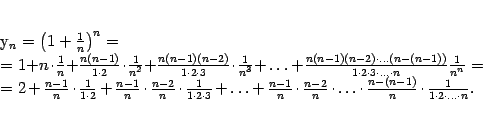
Покажем, что последовательность 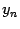ограничена сверху. Для этого заменим все дроби 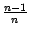, , 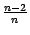..., 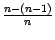на 1. Все эти дроби меньше 1, так что сумма в правой части формулы (Доказательство теоремы 2.15) увеличится:

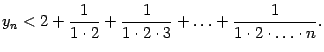
Далее, заменим все числа 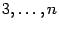в знаменателях этих слагаемых на 2; от этого правая часть ещё увеличится. Получим:

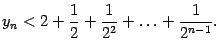
В правой части получилась сумма членов геометрической прогрессии. Она равна

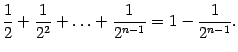
Поэтому

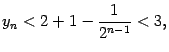
что и означает ограниченность последовательности сверху числом 3.

Покажем теперь, что последовательность 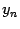не убывает. Действительно, запишем формулу (Доказательство теоремы 2.15) в виде

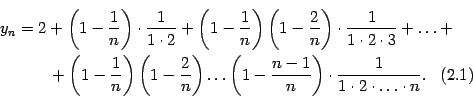
В аналогичной формуле, написанной для 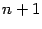вместо 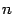, во-первых, увеличится каждое из выражений в круглых скобках (так как вычитаемое уменьшится) и, значит, увеличатся все слагаемые, содержащие такие скобки. Во-вторых, число слагаемых увеличится на одно: добавится положительное слагаемое

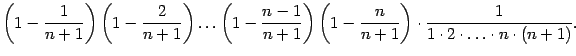
Следовательно, при росте номера 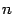члены последовательности 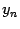строго возрастают: 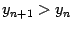при всех .

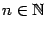Применим теперь к возрастающей ограниченной сверху последовательности 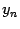теорему о пределе монотонной ограниченной функции ( теорема 2.13) и получим, что существует предел

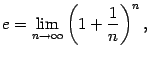
причём число 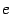не больше постоянной 3, ограничивающей последовательность. Осталось заметить, что 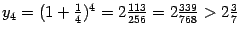. Так как все последующие члены 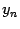ещё больше, то и предел 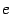, на основании теоремы о переходе к пределу в неравенстве ( следствие 2.7), не меньше числа 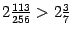, что и завершает доказательство теоремы.

Замечание 2.7 Можно также показать, что

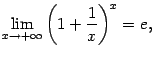(2.5)

однако строгое доказательство достаточно тяжело, и мы его здесь пропускаем.

В формуле (2.5) можно сделать замену 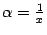, при этом база 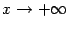перейдёт в базу 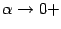, и мы получим

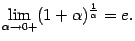
18 ВОПРОС:

Асимптота

• 

Рис. 1 Асимптота. Рис.

• 

Рис. 2 Асимптота. Рис.

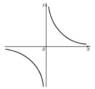
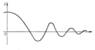
Асимптота (от греч. asymptotos — несовпадающий) кривой с бесконечной ветвью, прямая, к которой эта ветвь неограниченно приближается. Например, у гиперболы у = 1/х (рис. 1) асимптотами являются оси координат Ox и Оу. Кривая может пересекать свою А. (например, график затухающих колебаний,рис. 2). Кривые с бесконечными ветвями могут не иметь А. (например, у параболы нет. А.). Понятие А. играет важную роль в математическом анализе. Так, если график функции y = f(x) имеет А., определяемую уравнением у = ах + b, то эта функция может быть представлена в виде f(x) = ax + b + a(x), где a(х)®0при х ® ¥.

19 ВОПРОС:

Непрерывная функция

• 

Рис. 1 Непрерывная функция

• 

Рис. 2 Непрерывная функция

• 

Рис. 3 Непрерывная функция

1–3 из 4

Непрерывная функция, функция, получающая бесконечно малые приращения при бесконечно малых приращениях аргумента. Однозначная функция f (x) называется непрерывной при значении аргумента x₀, если для всех значений аргумента х, отличающихся достаточно мало от x₀, значения функции f (x) отличаются сколь угодно мало от её значения f (x₀). Точнее, функция f (х) называется непрерывной при значении аргумента x₀ (или, как говорят, в точке x₀), если каково бы ни было e > 0, можно указать такое d > 0, что при |х — х₀| < d будет выполняться неравенство |f (x) — f (x₀)| < e. Это определение равносильно следующему: функция f (x) непрерывна в точке x₀, если при х, стремящемся к x₀, значение функции f (x) стремится к пределу f (x₀). Если все условия, указанные в определении Н. ф., выполняются только при х ³ х₀ или только при х £ х₀, то функция называется, соответственно, непрерывной справа или слева в точке x₀. Функция f (x) называется непрерывной н а отрезке [а, b], если она непрерывна в каждой точке х при а < х < b и, кроме того, в точке а непрерывна справа, а в точке b — слева.

Понятию Н. ф. противопоставляется понятие разрывной функции. Одна и та же функция может быть непрерывной для одних и разрывной для других значений аргумента. Так, дробная часть числа х [её принято обозначать через (х)], например

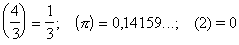
является функцией разрывной при любом целом значении и непрерывной при всех других значениях (рис. 1), причём в целочисленных точках она непрерывна справа.

Простейшими функциями переменного х, непрерывными при всяком значении x, являются многочлены, синус (у =sin x), косинус (у = cos x), показательная функция (у = a^x, где а — положительное число). Сумма, разность и произведение Н. ф. снова дают Н. ф. Частное двух Н. ф. также есть Н. ф., за исключением тех значений х, для которых знаменатель обращается в нуль (так как в таких точках рассматриваемое частное не определено). Например,

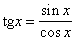
есть Н. ф. для всех значений х, кроме нечётных кратных p/2, при которых cosх обращается в нуль.

Н. ф. обладают многими важными свойствами, которыми и объясняется огромное значение этих функций в математике и её приложениях. Одно из важнейших свойств выражается следующей теоремой: для всякой функции, непрерывной на отрезке [а, b] можно найти многочлен, значения которого отличаются на этом отрезке от значений функции менее чем на произвольно малое, наперёд заданное число (теорема о приближении Н. ф. многочленами). Справедлива также и обратная теорема: всякая функция, которую на некотором отрезке можно с произвольной степенью точности заменить многочленом, непрерывна на этом отрезке.

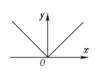
Функция, непрерывная на отрезке, ограничена на нём и достигает на этом отрезке наибольшего и наименьшего значения (см. Наибольшее и наименьшее значения функций). Кроме того, она принимает на этом отрезке все значения, лежащие между её наименьшим и наибольшим значениями. Функции, непрерывные на отрезке, обладают свойством равномерной непрерывности. Всякая функция, непрерывная на некотором отрезке, интегрируема на нём, т. е. является производной другой Н. ф. Однако не всякая Н. ф. сама имеет производную. Геометрически это означает, что график Н. ф. не обязательно обладает в каждой точке определённым направлением (касательной); это может произойти, например, потому, что график имеет угловую точку (рис.2, функция у = |x|), или потому, что он совершает в любой близости точки О бесконечно много колебаний между двумя пересекающимися прямыми (рис. 3, функция

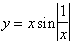
при х ¹ 0 и y = 0 при x = 0).

Существуют Н. ф., не имеющие производной ни в одной точке (первый пример такого рода был найден Б. Больцано). Представление о графике подобной функции даёт рис. 4, где изображены первые этапы построения, состоящего в неограниченно продолжающейся замене средней трети каждого прямолинейного отрезка двузвенными ломаными; соотношения длин подбираются так, чтобы в пределе получить Н. ф.

Функция F (x, у, z,...) нескольких переменных, определённая в некоторой окрестности точки (x₀, y₀, z₀,...), называется непрерывной в этой точке, если для любого e > 0 можно указать такое d > О, что при одновременном выполнении неравенств: |x — x₀| < d, |у — у₀|< d, |z — z₀| < d,... выполняется также и неравенство:

IF (x, у, z,...) — F (x₀, y₀, z₀,...)| < e.

Такая функция будет непрерывной по отношению к каждому аргументу в отдельности (если остальным аргументам приданы определённые числовые значения). Обратное, однако, неверно: функция F (x:, у, z,...), непрерывная по каждому аргументу в отдельности, может и не быть Н. ф. этих аргументов. Простейший пример этого даёт функция F (x, у), равная xy/(x² + y²), если x² + y² ¹ 0, и равная 0 при x = у = 0. Она непрерывна по x при любом фиксированном значении y по y — при любом фиксированном значении х. В частности, она непрерывна по x при у = 0 и по y при x = 0. Если же положить, например, у = х ¹ 0, то значение функции будет оставаться равным x²/(x² + y²)= ¹/₂, т. е. нельзя будет указать такого числа d > 0, чтобы при одновременном выполнении неравенств |х|< d, |у| < d выполнялось неравенство |ху/(х² + y²)| < e. На Н. ф. нескольких переменных распространяются все основные теоремы, относящиеся к Н. ф. одного переменного.

21 ВОПРОС:

Производная

Производная, основное понятие дифференциального исчисления, характеризующее скорость изменения функции; П. есть функция, определяемая для каждого х как предел отношения: 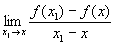, если он существует. Функцию, имеющую П., называют дифференцируемой.

Всякая дифференцируемая функция непрерывна; обратное утверждение неверно: существуют даже непрерывные функции, не имеющие П. ни в одной точке (см. Непрерывная функция). Для функций действительного переменного сама П. может быть недифференцируемой и даже разрывной. В комплексной же области существование первой П. влечёт существование П. всех порядков. О П. функций многих переменных (частная П.), а также о правилах нахождения П. и различных приложениях см. в ст. Дифференциальное исчисление.

В теории функций действительного переменного изучаются, в частности, функциональные свойства П. и различные обобщения понятия "П.". Так, например, всюду существующая П. относится к функциям первого класса по Бэра классификации; П. (даже если она разрывна) принимает все промежуточные значения между наименьшим и наибольшим. Из различных обобщений понятия "П." наиболее существенны следующие.

Производные числа. Верхним правым производным числом D_d называют верхний предел отношения 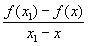при 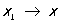, где x₁ > х. Аналогично определяют нижнее правое l_d, верхнее D_s и нижнее l_s левые производные числа. Если D_d = l_d (D = l_s), то f (x) имеет в точке х одностороннюю правую (левую) П. Обыкновенная П. существует, если все четыре производных числа конечны и совпадают. Производные числа были введены итал. математиком У. Дини (1878). Как показал Н. Н. Лузин (1915), если все четыре производных числа конечны на некотором множестве, то функция имеет обычную П. всюду на этом множестве, кроме точек множества меры нуль (см. Мера множества).

Асимптотическая (или аппроксимативная) производная была введена А. Я. Хинчиным(1916). Асимптотической П. называется предел отношения 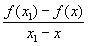, когда x₁ ® x пробегая точки множества, для которого х является плотности точкой.

22 ВОПРОС:

Дифференциал функции

Функция 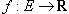называется дифференцируемой в точке 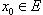, предельной для множества E, если ее приращение Δf(x₀), соответствующее приращению аргумента x, может быть представлено в виде

Δf(x₀) = A(x₀)(x - x₀) + ω(x - x₀), (1)

где ω(x - x₀) = о(x - x₀) при x → x₀.

Отображение 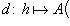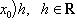, называется дифференциалом функции f в точке x₀, а величина A(x₀)h - значением дифференциала в этой точке.

Для значения дифференциала функции f принято обозначение df или df(x₀), если требуется знать, в какой именно точке он вычислен. Таким образом,

df(x₀) = A(x₀)h.

Разделив в (1) на x - x₀ и устремив x к x₀, получим A(x₀) = f'(x₀). Поэтому 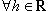имеем

df(x₀) = f'(x₀)h. (2)

Сопоставив (1) и (2), видим, что значение дифференциала df(x₀) (при f'(x₀) ≠ 0) есть главная часть приращения функции f в точке x₀, линейная и однородная в то же время относительно приращения h = x - x₀.