Какие матрицы можно складывать? Как сложить две матрицы? Как умножить матрицу на число? При каком условии на размерности матриц их произведение определено?

Вопросы к экзамену по математике

1. Определители и их свойства.
2. Матрицы и арифметические действия над ними.

3. Как вычислить определители первого и второго порядков? Что такое минор элемента определителя? Что такое алгебраическое дополнение элемента определителя?

4. Как вычислить определитель произвольного порядка разложением по строке, разложением по столбцу? Сформулируйте правило треугольников для определителей третьего порядка.

5. Какие матрицы можно складывать? Как сложить две матрицы? Как умножить матрицу на число? При каком условии на размерности матриц их произведение определено?

1. Как умножить матрицу на матрицу? Верно ли равенство А В = В А для произвольных матриц подходящей размерности? Как транспонировать матрицу?

7. Что такое обратная матрица? Может ли иметь обратную матрицу прямоугольная матрица, квадратная матрица с нулевым определителем? Перечислите в порядке их выполнения действия по нахождению обратной матрицы.

8. Что называется решением системы уравнений? Какие системы уравнений называются совместными, несовместными, определенными, неопределенными, однородными, неоднородными?

9. Какие системы уравнений можно решить по правилу Крамера и матричным методом? Какие нельзя?

10. Какие преобразования системы уравнений называются элементарными? К какому виду следует стремиться привести систему уравнений при ее решении методом Гаусса? Как получить решение системы, приведенной к треугольному виду, к виду трапеции?

1. Определите понятие декартовой системы координат на плоскости. Сколько координат характеризуют положение точки в пространстве? Как называются координаты точки?
2. Координаты и длина вектора. Направляющие косинусы вектора.
3. Линейные операции над векторами.
4. Деление отрезка в заданном отношении.
5. Уравнения прямой на плоскости.
6. Угол между прямыми на плоскости. Условия параллельности и перпендикулярности двух прямых.
7. Расстояние от точки до прямой.
8. Определение функции. Способы задания функции.
9. Предел функции. Свойства пределов.
10. Непрерывность функции.
11. Раскрытие неопределенностей вида и .
12. Понятие производной.
13. Правила дифференцирования.
14. Производные основных элементарных функций.
15. Правило дифференцирования сложной функции.
16. Первообразная и неопределенный интеграл. Основные свойства.
17. Область определения функции.
18. Дифференциал функции и его геометрический смысл. Связь с производной.
19. Таблица основных интегралов.
20. Методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям.
21. Определенный интеграл. Определение, геометрический смысл, свойства.
22. Формула Ньютона-Лейбница. Замена переменной и интегрирование по частям в определенном интеграле.

1. Определители и их свойства.

Определитель (детерминант) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы.

Обозначение определителя:

|A| = det A = ∆ A

aij — элементы определителя.

i- номер строки;

j- номер столбца;

Определитель первого порядка:

|A| = |a11|

Определитель второго порядка:

|a11 a12|

|a21 a22|

Определитель третьего порядка:

|a11 a12 a13|

|a21 a22 a23|

|a31 a32 a33|

Свойства определителя:

l Определитель не изменяется, если его стороны и его столбцы поменять местами:

|1 2| = |1 3|

|3 4| |2 4|

l Общий множитель элементов какой-либо строки (столбца) можно вынести за знак определителя:

|1 5| = 5 |1 1| =10 |1 1|

|2 10| |2 2| |1 1|

l При перестановки 2-х строк (столбцов) местами, определитель меняет свой знак на противоположный:

|1 2 3| |4 5 6| |5 4 6|

|4 5 6| = -|1 2 3| =|2 1 3|

|7 8 9| |7 8 9| |8 7 9|

l Определитель равен нулю, если он содержит:

а) строку (столбец) состоящий из нулей;

б) одинаковые строки (столбцы);

в) пропорциональные строки (столбцы);

l Если элементы какой-либо строки (столбца) определителя представить собой сумму двух слагаемых, то определитель может быть представлен в виде двух соответствующих определителей:

|a11 a12+b a13| |a11 a12 a13| |a11 b a13|

|a21 a22+c a23| = |a21 a22 a23| = |a21 c a23|

|a31 a32+d a33| |a31 a32 a33| |a31 d a33|

l Определитель не изменяется, если по всем элементам какой-либо строки (столбца) прибавить соответствующие элементы любой другой строки (столбца), умноженной на постоянно число.

1. Матрицы и арифметические действия над ними.

Матрицей А называется прямоугольная таблица числе, состоящая из m строк и n столбцов и имеющего следующий вид:

А = (a11 a12 ... a1n)

(a21 a22 ... a2n) mxn

(.......................)

(am1 am2..amn)

Квадратная матрицы, у которой на главной диагонали расположены только «1», а все остальные элементы «0», называется единичной:

E = (1 0)

(0 1)

E = (1 0 0)

(0 1 0)

(0 0 1)

Матрица, у которой все элементы равны нулю, называется нулевой.

Матрицы, содержащая только одну строку, называется «вектор строка», иначе «вектор столбец.

Матрицы можно складывать, умножать на число, перемножать.

Суммой двух матриц A и B, называется матрицей С, каждый элемент который равен сумме соответствующих элементов матриц слагаемых. Складывать можно только одинакового размера.

Произведением матрицы A на число = С, каждый элемент которой равен произведению элемента матрицы А на число.

1. Как вычислить определители первого и второго порядков? Что такое минор элемента определителя? Что такое алгебраическое дополнение элемента определителя?

Вычисление определителя первого порядка:

A = |a11| = a11

Вычисление определителя второго порядка:

A = |a11 a12| = a11*a22 - a21*a12

|a21 a22|

Минором называется определитель второго порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которой расположен элемент aij:

|a11 a12 a13|

|a21 a22 a23| M33 = |a11 a12|

|a31 a32 a33| |a21 a22|

Алгебраическим дополнением Aij, называется произведением:

Aij = (-1)^i+j * Mij

A11 = (-1)^1+1 * M11= M11 = |a22 a23|

|a32 a33|

A23 = (-1)^2+3 * M23 = -M23 = - |a11 a12|

|a31 a32|

1. Как вычислить определитель произвольного порядка разложением по строке, разложением по столбцу? Сформулируйте правило треугольников для определителей третьего порядка.

Теорема о разложении определителя.

Определитель равен сумме произведений элементов некоторой строки (столбца) на соответствующие им алгебраические дополнения.

|a11 a12 a13|

|a21 a22 a23| = a11*A11 + a12*A12+a13*A13 = a12*A12 + a22*A22+a32*A32

|a31 a32 a33|

Правило треугольников для определителей третьего порядка.

Со знаком плюс идут произведения троек чисел, расположенных на главной диагонали матрицы, и в вершинах треугольников с основанием параллельным этой диагонали и вершиной в противоположного угла матрицы. Со знаком минус идут тройки из второй диагонали и из треугольников, построенных относительно этой диагонали. Следующая схема демонстрирует это правило, называемое правилом треугольников.

Что такое обратная матрица? Может ли иметь обратную матрицу прямоугольная матрица, квадратная матрица с нулевым определителем? Перечислите в порядке их выполнения действия по нахождению обратной матрицы.

Обратная матрица, это такая матрица A^−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E.

Прямоугольная матрица и квадратная матрица с нулевым определителем не может быть обратима.

Для нахождения обратной матрицы нужно выполнить следующие действия:

- Найти определитель квадратной матрицы, если |A| неравен нулю, то такая матрица обратима;

- Поделить единицу на определитель матрицы и умножить на саму матрицу;

- Сделать проверку, т.е. перемножить обратную матрицу и саму матрицу, в результате чего должна получиться единичная матрица E.

Непрерывность функции.

Функция y = f(x) непрерывная в точке x=x0, если:

1) Эта функция определена в точке x=x0;

2) Приращение функции в точке x0->0 при ∆x->0

lim (∆x->0) ∆y = 0

lim (∆x->0) (f(x0 + ∆x) — f(x0) ) = 0

y = f(x) называется непрерывной в данной точке х0, если её предел в точке х0 существует и равен значению функции на этой точке:

lin(x->x0) f(x) = f(x0)

Свойства непрерывной функции:

- Если функция f1(x) и f2(x) непрерывны в точке а, то:

а) Их сумма, разность, произведение являются непрерывными функциями в этой точке;

б) Частный f1(x)/f2(x) являются непрерывной функцией, при условии, что f2(x) не равно а

- Каждая элементарная функция непрерывна на своей области определения

1. Раскрытие неопределенностей вида 0/0 и беск/беск.

Неопределенности типа

Пусть заданы две функции f (x) и g (x), такие, что

В этом случае говорят, что функция имеет неопределенность типа в точке x = a. Чтобы

найти предел при x = a когда функция содержит неопределенность , нужно

разложить на множители числитель и/или знаменатель и затем сократить члены, стремящиеся к нулю.

Неопределенности типа

Пусть две функции f (x) и g (x) обладают свойством

где a является действительным числом, либо стремится к + ∞ или − ∞. Говорят, что в этом

случае функция имеет в точке a неопределенность типа .

Для вычисления предела в этой точке необходимо разделить числитель и знаменатель на x в наивысшей степени.

Понятие производной.

Производная — функция, являющаяся результатом применения той или иной операции дифференцирования к исходной функции.

1. Правила дифференцирования.

(const)'=0

(c*u)'=c*u'

(u+-v)'=u'+-v'

(u*v)'=u'*v+u*v'

(u/v)'=(u'*v-u*v')/v^2 ; v=/0

1. Производные основных элементарных функций.

Y = (lgx) y' = 1/x

Таблица основных интегралов.

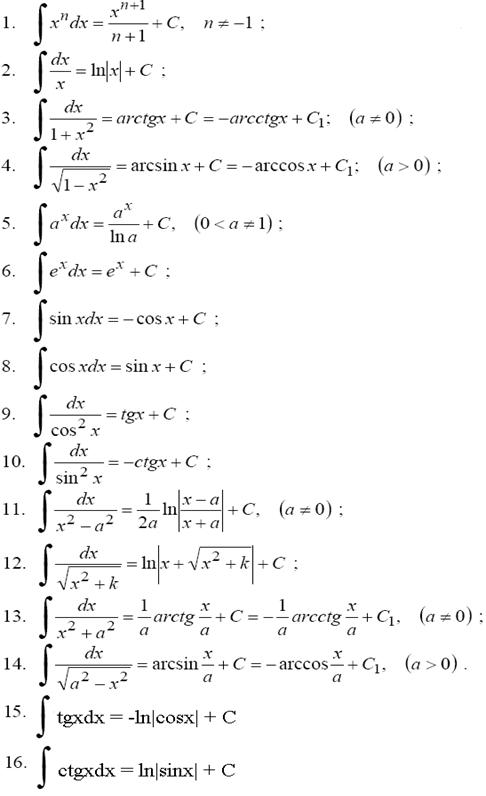
Вопросы к экзамену по математике

1. Определители и их свойства.
2. Матрицы и арифметические действия над ними.

3. Как вычислить определители первого и второго порядков? Что такое минор элемента определителя? Что такое алгебраическое дополнение элемента определителя?

4. Как вычислить определитель произвольного порядка разложением по строке, разложением по столбцу? Сформулируйте правило треугольников для определителей третьего порядка.

5. Какие матрицы можно складывать? Как сложить две матрицы? Как умножить матрицу на число? При каком условии на размерности матриц их произведение определено?

1. Как умножить матрицу на матрицу? Верно ли равенство А В = В А для произвольных матриц подходящей размерности? Как транспонировать матрицу?

7. Что такое обратная матрица? Может ли иметь обратную матрицу прямоугольная матрица, квадратная матрица с нулевым определителем? Перечислите в порядке их выполнения действия по нахождению обратной матрицы.

8. Что называется решением системы уравнений? Какие системы уравнений называются совместными, несовместными, определенными, неопределенными, однородными, неоднородными?

9. Какие системы уравнений можно решить по правилу Крамера и матричным методом? Какие нельзя?

10. Какие преобразования системы уравнений называются элементарными? К какому виду следует стремиться привести систему уравнений при ее решении методом Гаусса? Как получить решение системы, приведенной к треугольному виду, к виду трапеции?

1. Определите понятие декартовой системы координат на плоскости. Сколько координат характеризуют положение точки в пространстве? Как называются координаты точки?
2. Координаты и длина вектора. Направляющие косинусы вектора.
3. Линейные операции над векторами.
4. Деление отрезка в заданном отношении.
5. Уравнения прямой на плоскости.
6. Угол между прямыми на плоскости. Условия параллельности и перпендикулярности двух прямых.
7. Расстояние от точки до прямой.
8. Определение функции. Способы задания функции.
9. Предел функции. Свойства пределов.
10. Непрерывность функции.
11. Раскрытие неопределенностей вида и .
12. Понятие производной.
13. Правила дифференцирования.
14. Производные основных элементарных функций.
15. Правило дифференцирования сложной функции.
16. Первообразная и неопределенный интеграл. Основные свойства.
17. Область определения функции.
18. Дифференциал функции и его геометрический смысл. Связь с производной.
19. Таблица основных интегралов.
20. Методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям.
21. Определенный интеграл. Определение, геометрический смысл, свойства.
22. Формула Ньютона-Лейбница. Замена переменной и интегрирование по частям в определенном интеграле.

1. Определители и их свойства.

Определитель (детерминант) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы.

Обозначение определителя:

|A| = det A = ∆ A

aij — элементы определителя.

i- номер строки;

j- номер столбца;

Определитель первого порядка:

|A| = |a11|

Определитель второго порядка:

|a11 a12|

|a21 a22|

Определитель третьего порядка:

|a11 a12 a13|

|a21 a22 a23|

|a31 a32 a33|

Свойства определителя:

l Определитель не изменяется, если его стороны и его столбцы поменять местами:

|1 2| = |1 3|

|3 4| |2 4|

l Общий множитель элементов какой-либо строки (столбца) можно вынести за знак определителя:

|1 5| = 5 |1 1| =10 |1 1|

|2 10| |2 2| |1 1|

l При перестановки 2-х строк (столбцов) местами, определитель меняет свой знак на противоположный:

|1 2 3| |4 5 6| |5 4 6|

|4 5 6| = -|1 2 3| =|2 1 3|

|7 8 9| |7 8 9| |8 7 9|

l Определитель равен нулю, если он содержит:

а) строку (столбец) состоящий из нулей;

б) одинаковые строки (столбцы);

в) пропорциональные строки (столбцы);

l Если элементы какой-либо строки (столбца) определителя представить собой сумму двух слагаемых, то определитель может быть представлен в виде двух соответствующих определителей:

|a11 a12+b a13| |a11 a12 a13| |a11 b a13|

|a21 a22+c a23| = |a21 a22 a23| = |a21 c a23|

|a31 a32+d a33| |a31 a32 a33| |a31 d a33|

l Определитель не изменяется, если по всем элементам какой-либо строки (столбца) прибавить соответствующие элементы любой другой строки (столбца), умноженной на постоянно число.

1. Матрицы и арифметические действия над ними.

Матрицей А называется прямоугольная таблица числе, состоящая из m строк и n столбцов и имеющего следующий вид:

А = (a11 a12 ... a1n)

(a21 a22 ... a2n) mxn

(.......................)

(am1 am2..amn)

Квадратная матрицы, у которой на главной диагонали расположены только «1», а все остальные элементы «0», называется единичной:

E = (1 0)

(0 1)

E = (1 0 0)

(0 1 0)

(0 0 1)

Матрица, у которой все элементы равны нулю, называется нулевой.

Матрицы, содержащая только одну строку, называется «вектор строка», иначе «вектор столбец.

Матрицы можно складывать, умножать на число, перемножать.

Суммой двух матриц A и B, называется матрицей С, каждый элемент который равен сумме соответствующих элементов матриц слагаемых. Складывать можно только одинакового размера.

Произведением матрицы A на число = С, каждый элемент которой равен произведению элемента матрицы А на число.

1. Как вычислить определители первого и второго порядков? Что такое минор элемента определителя? Что такое алгебраическое дополнение элемента определителя?

Вычисление определителя первого порядка:

A = |a11| = a11

Вычисление определителя второго порядка:

A = |a11 a12| = a11*a22 - a21*a12

|a21 a22|

Минором называется определитель второго порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которой расположен элемент aij:

|a11 a12 a13|

|a21 a22 a23| M33 = |a11 a12|

|a31 a32 a33| |a21 a22|

Алгебраическим дополнением Aij, называется произведением:

Aij = (-1)^i+j * Mij

A11 = (-1)^1+1 * M11= M11 = |a22 a23|

|a32 a33|

A23 = (-1)^2+3 * M23 = -M23 = - |a11 a12|

|a31 a32|

1. Как вычислить определитель произвольного порядка разложением по строке, разложением по столбцу? Сформулируйте правило треугольников для определителей третьего порядка.

Теорема о разложении определителя.

Определитель равен сумме произведений элементов некоторой строки (столбца) на соответствующие им алгебраические дополнения.

|a11 a12 a13|

|a21 a22 a23| = a11*A11 + a12*A12+a13*A13 = a12*A12 + a22*A22+a32*A32

|a31 a32 a33|

Правило треугольников для определителей третьего порядка.

Со знаком плюс идут произведения троек чисел, расположенных на главной диагонали матрицы, и в вершинах треугольников с основанием параллельным этой диагонали и вершиной в противоположного угла матрицы. Со знаком минус идут тройки из второй диагонали и из треугольников, построенных относительно этой диагонали. Следующая схема демонстрирует это правило, называемое правилом треугольников.

Какие матрицы можно складывать? Как сложить две матрицы? Как умножить матрицу на число? При каком условии на размерности матриц их произведение определено?

Складывать можно только матрицы одного размера:

(a11 a12) (b11 b12)

(a21 a22) + (b21 b22)

(a31 a32) (b31 b32)

Пример:

(1 4) (-7 -5) (-6 -1)

(2 5) + (-1 0) = ( 1 5)

(3 6) ( 6 3) ( 9 9)

Умножение матрицы на число. Нужно умножить каждый элемент матрицы на это число:

( 1 4) ( 3 12)

3* ( 2 5) = ( 6 15)

(-1 -3) (-3 -9)

Чтобы получить произведение матриц ABнеобходимо чтобы количество столбцов матрицы Aбыло равно количеству строк матрицы B. Если условие выполняется, произведение матриц определено. Рассмотрим представленные ниже матрицы Aи B, с размерностью 2 × 3 и 3 × 3 соответственно:

Произведение ABопределено поскольку количество столбцов матрицы Aравно количеству строк матрицы B. Что произведение BA, получаемое в результате перестановки множителей, не определено, потому что количество столбцов матрицы Bне равно количеству строк матрицы A.

6. Как умножить матрицу на матрицу? Верно ли равенство А В = В А для произвольных матриц подходящей размерности? Как транспонировать матрицу?

Перемножить матрицы можно только в том случае, если они подходят по размерности, т.е. количество строк первой матрицы должно быть равно количеству столбцов второй матрицы. Произведением является сумма произведений элемента каждой строки первой матрицы на каждый элемент столбца второй матрицы. Например:

(1 2 -1) (-1 1)

(3 1 -2) * (2 -2) = (1*(-1)+4+(-2) 1+(-4) + (-1) ) (1 - 4)

(2 1) (-3+2+(-4) 3+(-2)+(-2) ) = (-5 -1)

Равенство АВ = ВА для матриц подходящих по размерности не верно.

Транспонирование матрицы осуществляется путем перестановки ее строк и столбцов. Следовательно, результатом транспонирования матрицы m×n будет матрица n×m. Результат транспонирования матрицы Mмы будем обозначать MT

M = (1 2) MT= (1 3 5)

(3 4) (2 4 6)

(5 6)

Что такое обратная матрица? Может ли иметь обратную матрицу прямоугольная матрица, квадратная матрица с нулевым определителем? Перечислите в порядке их выполнения действия по нахождению обратной матрицы.

Обратная матрица, это такая матрица A^−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E.

Прямоугольная матрица и квадратная матрица с нулевым определителем не может быть обратима.

Для нахождения обратной матрицы нужно выполнить следующие действия:

- Найти определитель квадратной матрицы, если |A| неравен нулю, то такая матрица обратима;

- Поделить единицу на определитель матрицы и умножить на саму матрицу;

- Сделать проверку, т.е. перемножить обратную матрицу и саму матрицу, в результате чего должна получиться единичная матрица E.