Переменные и постоянные величины

Переменные и постоянные величины

Переменные величины — это такие величины, которые в условиях данного вопроса могут принимать различные значения

Переменные величины, как правило, обозначаются последними буквами латинского алфавита x, y, z.

Постоянные величины — это такие величины, которые в условиях данного вопроса сохраняют неизменные значения.

Постоянные — первыми a, b, c.

Например в различных функциях используют переменные и постоянные величины:

В квадратном уравнении

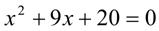
X является переменной величиной, а 9,20 и 0 постоянными величинами.

Понятие окрестности точки. Точки прикосновения, предельные , граничные и внутренние точки множества.

Окрестность точки — множество, содержащее данную точку, и близкие (в каком-либо смысле) к ней.

Проколотой окрестностью точки называется окрестность точки, из которой исключена эта точка.

Точка x топологического пространства X называется точкой прикосновения множества S если любая окрестность x содержит хотя бы одну точку множества S.

Точка Р называется предельной точкой множества М, если в любой окрестности точки Р имеется, по крайней мере, ещё одна точка множества М, кроме точки Р.

Внутренняя точка множества в топологии есть точка, входящая в данное множество вместе с некоторой своей окрестностью.

Граничная точка множества – точка пространства, любая (открытая) окрестность которой содержит как точки, принадлежащие рассматриваемому множеству, так и не принадлежащие ему точки (точки его дополнения).

Граничная точка множества может как принадлежать, так и не принадлежать этому множеству.

Открытые и замкнутые множества. Отрезок, интервал, промежуток действительной прямой. Ограниченные множества.

Множество M на прямой называется открытым, если каждая его точка сожержится в этом множестве вместе с некоторым интервалом. Замкнутым называется множество, содержащее все свои предельные точки (т. е. такие, что любой интервал, содержащий эту точку, пересекается со множеством еще хотя бы по одной точке). Например, отрезок является замкнутым множеством, но не является открытым, а интервал, наоборот, является открытым множеством, но не является замкнутым.

Отрезок прямой — часть прямой, ограниченная двумя точками.

Интервал —множество всех чисел, удовлетворяющих строгому неравенству а<x<b, называется интервалом (a,b)

Ограниченное множество — множество, которое в определенном смысле имеет конечный размер

Ограниченные и монотонные последовательности

Ограниченная последовательность — это последовательность элементов множества X, все члены которой не превышают некоторого элемента из этого множества. Этот элемент называется гранью данной последовательности.

Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают. Подобные последовательности часто встречаются при исследованиях и имеют ряд отличительных особенностей и дополнительных свойств. Последовательность из одного числа не может считаться возрастающей или убывающей.

Предел функции

Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к данной точке.

Предел функции является обобщением понятия предела последовательности: изначально под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.

Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).

Предел сложной функции

Если функция y=f(x) имеет в точке a конечный предел b и не принимает значение b в некоторой проколотой окрестности U(a) этой точки, а функция g(y) имеет в точке конечный предел c, то сложная функция g(f(x)) имеет предел в точке a и он равен c.

Односторонние пределы

Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева) и правосторонним пределом (пределом справа).

Предел монотонной функции.

Монотонная функция — это функция, приращение которой не меняет знака, то есть либо всегда не отрицательное, либо всегда не положительное. Если в дополнение приращение не равно нулю, то функция называется строго монотонной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.

Если функция f(x) определена и монотонна на отрезке [a;b], то в каждой точке x 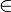(a;b) эта функция имеет конечные пределы слева и справа, а в точках a и b правосторонний и левосторонний пределы.

Замечательные пределы

Замечательные пределы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:

Первый замечательный предел:

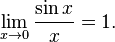
Второй замечательный предел:

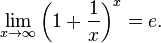
Таблица производных и дифференциалов основных элементарных функций.

Производные высших порядков

Асимптоты

Асимптота — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность.

Вертикальная асимптота — прямая вида 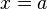при условии существования предела .

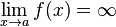Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:

1.

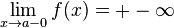
2.

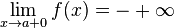
Замечание: обратите внимание на знаки бесконечностей в этих равенствах.

Горизонтальная асимптота — прямая вида 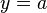при условии существования предела

.

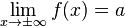Наклонная

Наклонная асимптота — прямая вида 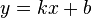при условии существования пределов

Пример наклонной асимптоты

1.

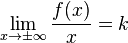
2.

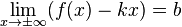
Замечание: функция может иметь не более двух наклонных (горизонтальных) асимптот.

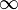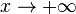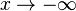Замечание: если хотя бы один из двух упомянутых выше пределов не существует (или равен ), то наклонной асимптоты при (или ) не существует.

Порядок нахождения асимптот

1. Нахождение вертикальных асимптот.

2. Нахождение двух пределов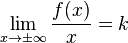

3. Нахождение двух пределов :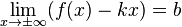

если 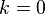в п. 2.), то 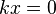, и предел 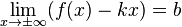находится по формуле горизонтальной асимптоты, .

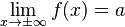Таблица неопределенных интегралов от основных элементарных функций.

Замена переменной

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (т. е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводащимся (в случае «удачной» подстановки). Общих методов подбора подстановок не существует. Умение правильно oпpeделить подстановку пpиобpетaeтcя практикой.

Пусть тpебyетcя вычислить интеграл 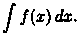Сделаем подстановку

х =φ(t), где φ(t) - функция, имеющая непрерывную производную.

Тогда dx=φ^'(t) dt и на основании свойства инвариантности формулы интегрирования неопpeделeннoгo интеграла получаем формулу интегриpoвaния подcтaнoвкoй

(30.1)

Формула (30.1) также называется формулой замены переменных в неопределeннoм интеграле. Пoслe нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования t назад к переменной х.

Иногда целесообразно подбирать подстановку в виде t= φ(х), тогда

Другими слoвaми, формулу (30.1) можно применять справа налево.

Определенный интеграл

Понятие определенного интеграла вводится следующим образом. Пусть на отрезке [a, b] определена функция f(x). Разобьем отрезок [a, b] на n частей точками a = x₀ < x₁ <...<x_n = b. Из каждого интервала (x_i-1, x_i) возьмем произвольную точку x_i и составим сумму f(x_i)Δ x_i, где
Δx_i = x_i - x_i-1. Сумма вида f(x_i)Δ x_i называется интегральной суммой, а ее предел при λ = max Δx_i→ 0, если он существует и конечен, называется определенным интегралом функции f(x) от a до b и обозначается:

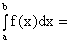
f(x_i)Δ x_i. (8.5)

Функция f(x) в этом случае называется интегрируемой на отрезке
[a, b],числа a и b носят название нижнего и верхнего предела интеграла.

Для определенного интеграла справедливы следующие свойства:

1) ;

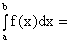
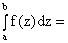
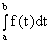2) ;

3) - ;

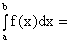4) 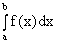, (k = const, k∈R);

5) ;

6) ;

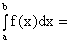
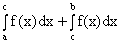7) 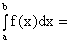f(ξ)(b-a) (ξ∈a,b]).

Последнее свойство называется теоремой о среднем значении.

Пусть f(x) непрерывна на [a, b]. Тогда на этом отрезке существует неопределенный интеграл

∫f(x) dx = F(x) + C

и имеет место формула Ньютона-Лейбница, cвязывающая определенный интеграл с неопределенным:

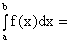F(b) - F(a). (8.6)

Геометрическая интерпретация: определенный интеграл 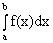представляет собой площадь криволинейной трапеции, ограниченной сверху кривой y= f(x), прямыми x = a и x = b и отрезком оси Ox.

Переменные и постоянные величины

Переменные величины — это такие величины, которые в условиях данного вопроса могут принимать различные значения

Переменные величины, как правило, обозначаются последними буквами латинского алфавита x, y, z.

Постоянные величины — это такие величины, которые в условиях данного вопроса сохраняют неизменные значения.

Постоянные — первыми a, b, c.

Например в различных функциях используют переменные и постоянные величины:

В квадратном уравнении

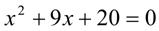
X является переменной величиной, а 9,20 и 0 постоянными величинами.