Системы линейных однородных уравнений
Определение 4.7. Система линейных уравнений вида:
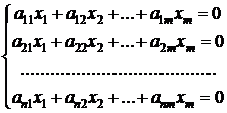 , | ( 4.7 ) |
называется однородной системой линейных уравнений, где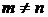 
.
Однородная система всегда имеет одно решение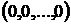 
, которое называется тривиальным.Условиясуществования нетривиальных решений определяется следующими теоремами.
Теорема 4.2. Система однородных линейных уравнений имеет нетривиальные решения тогда и только тогда, когда ранг ее матрицы меньше числа неизвестных.
Теорема 4.3. В случае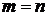 
система ( 4.7 ) имеет нетривиальное решение только тогда, когда ее определитель равен нулю.
Теорема 4.4. Любая линейная комбинация решений системы ( 4.7) также является решением этой системы.
Определение 4.8. Совокупность решений системы линейных однородных уравнений называется фундаментальной системой решений, если эта совокупность состоит из линейно независимых решений и любое решение системы является линейной комбинацией этих решений.
Теорема 4.5. Если ранг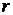 
матрицы системы ( 4.7) меньше числа неизвестных 
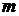, то существует фундаментальная система решений, состоящая из 
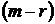решений.
Пример 4.15.Найти общее решение и одну из фундаментальных систем решений для следующей системы однородных уравнений:
.
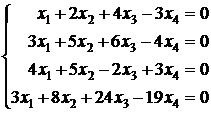Решение: 1) Найдем ранг матрицы. Не забываем, что преобразования можно проводить только со строками: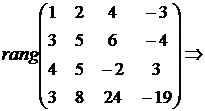 
{Преобразуем матрицу: умножим первую строку на (-3) и сложим со второй строкой, затем умножим первую строку на (-4) и сложим с третьей строкой, затем умножим первую строку на (-3) и сложим с четвертой строкой}
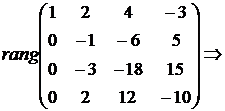{Вторая и четвертая, а также вторая и четвертая строки пропорциональны. Следовательно, третью и четвертую строки можно удалить} 
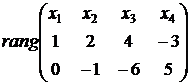, откуда 
.
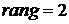2) За базисный минор возьмем определитель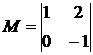 
. Он имеет наивысший порядок и отличен от нуля. В базисный минор вошли коэффициенты при переменных 
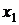и 
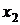, они составят группу зависимых переменных, следовательно, 
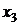и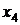 
составят группу свободных переменных.
3) Выразим зависимые переменные через свободные, таким образом, найдем общее решение системы: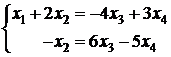 
.
Во втором уравнении умножим все коэффициенты на (-1) и подставим значение 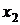из второго уравнения в первое, получим выражения 
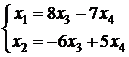. 4) Найдем фундаментальную систему решений. Она состоит из 
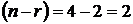решений, которые должны быть линейно независимыми. Самый простой способ составить линейно независимые строки в матрице решения это следующий: свободным переменным придают значения из строк определителя 
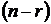-го порядка, отличного от нуля. Затем подставляют эти значения в выражения общего решения и определяют значения зависимых переменных. Простейшим определителем 2-го порядка, отличным от нуля является 
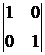. Подставим первый набор значений свободных переменных в решение: 
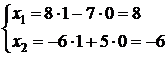, затем второй: 
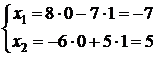. Откуда получаем фундаментальную систему решений: 
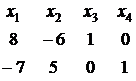. Ответ: общее решение системы: 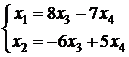; фундаментальная система решений: .
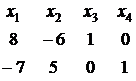Примеры решения типовых задач: системы линейных уравнений
Задача 4.1.Решить систему линейных уравнений методом Крамера:
.
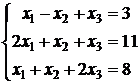Решение: 1)Составим определители, соответствующие исходной системе и каждому неизвестному:
; 
; 
; 
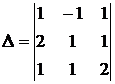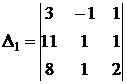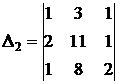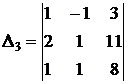
тогда решение можно будет определить по формулам Крамера.
2)Вычислим определитель системы: сложим соответствующие элементы первой и второй строк, затем первой и третьей, получим во втором столбце нули, кроме элемента в первой строке. Найдем определитель разложением по второму столбцу: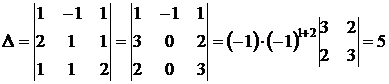 
.
Определитель ненулевой, значит, система имеет решение.
2)Вычислим оставшиеся определители:
;
;
.
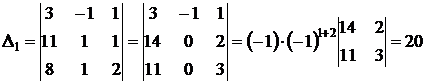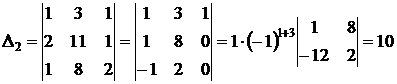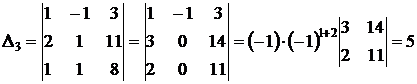Откуда решение системы:
; 
; 
.
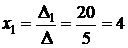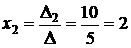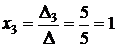3)Проверяем подстановкой полученных значений в исходную систему:
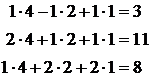. Ответ: 
; 
; 
.
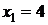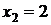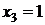Задача 4.2. Решить систему линейных уравнений матричным методом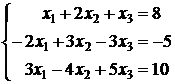 
.
Решение: Введем обозначения: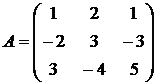 
; 
; 
.
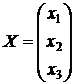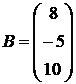тогда исходная система запишется в виде: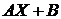 
, откуда решение определяется по формуле: 
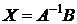. Определим обратную матрицу:
1) определитель матрицы определитель не равен нулю:
,
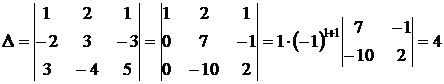следовательно, решение существует; 2) транспонируем матрицу:
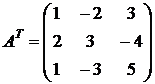; 3) находим алгебраические дополнения к каждому элементу: 
; 
; 
; 
; 
; 
; 
; 
; 
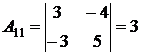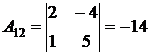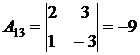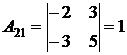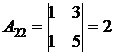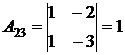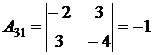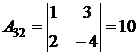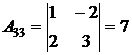; 4) обратная матрица формируется из алгебраических дополнений, записанных вместо элементов транспонированной матрицы, и деленных на определитель исходной матрицы: 
.
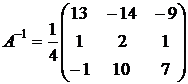Проверяем выполнение условия: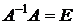 
:
.
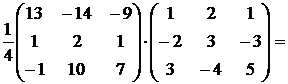
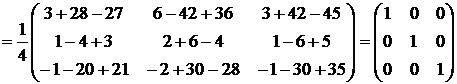Находим решение: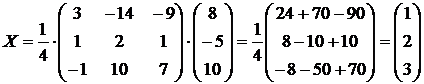 
.
Проверяем: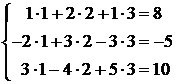 
. Ответ: 
; ; 
.
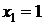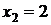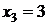Задача 4.3. Решить систему линейных уравнений методом Гаусса:
.
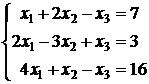Решение. Составим расширенную матрицу: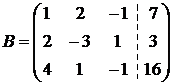 
.
Преобразуем матрицу так, чтобы исключить переменную 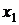из всех уравнений, кроме первого: умножим элементы первой строки на (-2) и сложим с соответствующими элементами второй строки, затем умножим элементы первой строки на (-4) и сложим с элементами третьей строки: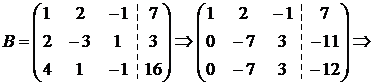 
Умножим элементы второй строки на (-1) и сложим с соответствующими элементами третьей строки: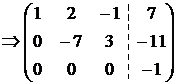 
. Уравнение, соответствующее третьей строке матрицы, противоречиво: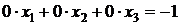 
или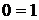 
, следовательно, система несовместна.
Ответ: система не имеет решений.
Задача 4.4. Решить систему линейных уравнений методом Гаусса:
.
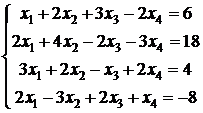Решение. 1)Составим расширенную матрицу: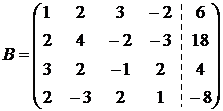 
.
2) Преобразуем ее так, чтобы исключить переменную 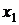из всех уравнений, кроме первого: умножим элементы первой строки на (-2) и сложим с соответствующими элементами второй строки; умножим элементы первой строки на (-3) и сложим с соответствующими элементами третьей строки; умножим элементы первой строки на (-2) и сложим с соответствующими элементами третьей строки: 
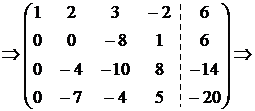{Поменяем местами вторую и четвертую строки} 
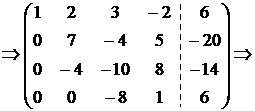{Умножим элементы второй строки на 
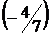и сложим с элементами третьей строки} 
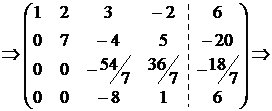{Умножим элементы третьей строки на 
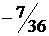и сложим с соответствующими элементами четвертой строки и переставим местами третий и четвертый столбцы}
.
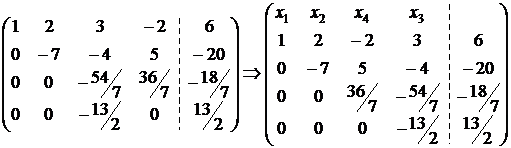Из последнего уравнения находим переменную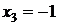 
.
6) Подставляя в третье уравнение значение переменной 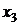находим значение переменной : 
.
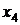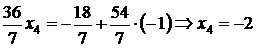7) Из соответствующих уравнений находим оставшиеся переменные:
;
.
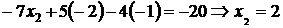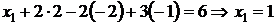8) Проверяем:
.
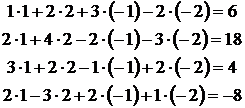Ответ: ; ; ;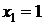 
.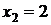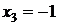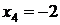